 (0.1)
(0.1)
「化学教育ジャーナル(CEJ)」第4巻第2号(通巻7号)発行2000年12月27日/採録
番号4-18/2000年12月 7日受理
URL = http://www.edu.utsunomiya-u.ac.jp/chem/cejrnl.html
吉村 洋介
京都大学理学部化学教室
E-mail: yoshimura.yosuke.6w@kyoto-u.jp
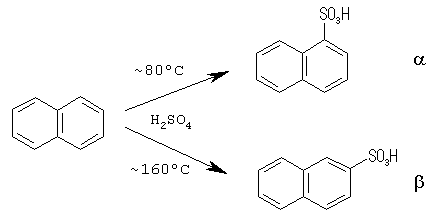
いくつかの化学種の間の複合反応の平衡と速度を取り扱う際には、単一の化学反応を扱うときとは質的に異なる問題と向き合うことになります。 端的なのは反応で複数の生成物が得られる場合、生成物の比が反応速度支配(kinetically controlled)か、熱力学支配(thermodynamically controlled)かという問題でしょう。 ナフタレンと硫酸の反応でナフタレンスルホン酸が生成する反応は、よく知られた例です:
 (0.1)
(0.1)
この反応では、反応温度が80℃ぐらいではα体が主生成物となり、160℃に上げるとβ体が主生成物となります。 これは、低温では不安定だが容易に生成するα体が(反応速度支配)、高温では安定だが生成速度の遅いβ体が主生成物となる(熱力学支配)わけです。
もう一つ多成分の化学種の間の反応速度と平衡を扱う上で重要なのものに「詳細釣り合い(detailed balance。あるいは微視的可逆性microscopic reversibility)の原理」があります [1, 2]。 よく取り上げられる例ですが、X、Y、Zという3種の分子種が、1次の反応速度則に従って互いに変化する、次のような反応を考えましょう。
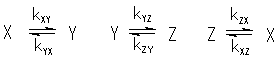 (0.2)
(0.2)
詳細釣り合いの原理はこの反応で、たとえばXとYだけ単独で取り出したとしても、速度定数と平衡濃度(添え字eで表すことにします)の間に
kXY [X]e = kYX [Y]e (0.3)
という関係が成り立つことを主張します。これは一見当たり前のようにも見えますが、自明なものではありません。
このような多数の化学種の間の反応速度と平衡に関して、学生諸君の注意を喚起する例として、古典的なコンピューターゲームであるテトリスに取材した問題を考えてみました。
ここで考えようとする問題は次のようなものです:
|
4個の正方形を、隣り合うもの同士、少なくとも一辺を共有するように組み合わせる。 ここで図形の裏返しを許さないと、次の7種類の図形ができる。 方眼紙の上にでたらめに正方形を配置して、この7種の図形を作ったとき、それぞれの図形の現れる確率を求めよ。 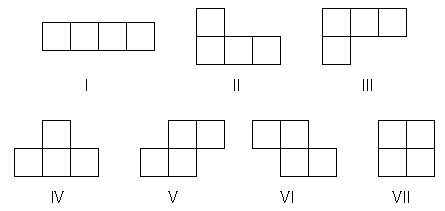
図1.4つの正方形を組み合わせてできる7つの図形 |
この問題を、みなさんならどのように解きますか?
ここで前章の問題について、2つの解答を紹介しましょう。
|
1つずつ、順に4個の正方形を貼り合わせていくプロセスを考えよう。 最初2個の正方形を置くまでは、一種類しか図形が現れないから特に考えるまでもない。 さて、正方形が2つからできた図形に新たに1個の正方形を付けるとすると、付ける場所には側面4ヶ所と端面2ヶ所の2種類あわせて6ヶ所ある。 これがそれぞれ同じように実現されるから、その結果できる図形A、Bは、Aが1/3、Bが2/3の確率で出現するはずだ。 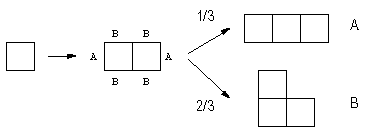
図2.正方形を順次貼り合わせて、図形を組み立てる。 2つ正方形からできる図形のAと付した場所に正方形を付ければ図形Aが、Bと付した場所に正方形を付ければ図形Bができる。 次にこの図形A、Bにもう1個正方形を加えよう。 Aについては4種類8ヶ所、Bには6種類7ヶ所に付けることができ、それぞれから先の7種類の図形が生成する。 図形A、Bが与えられれば、それぞれの場所には同じ確率で正方形が付くわけだから、たとえば図形IVについては図3のように構成していくことになる。 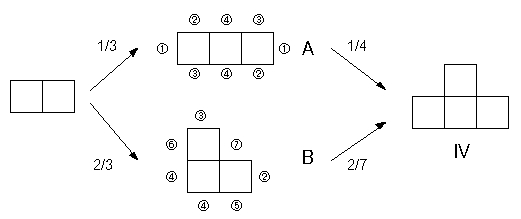
図3.図形IVを順次正方形を貼り付けて構成する過程。中間の3つの正方形からなる2つの図形で、(1)~(7)を付した場所に正方形を付けると、それぞれ図形I~VIIができる。 したがって、図形IVの出現確率は次のように計算できる:
(図形IVの出現確率) = (Aの出現確率)×(2/8) +(Bの出現確率)×(2/7) 他の図形も同様に計算でき、それぞれの出現確率は次のようになる:
|
|
ともかく、7つの図形を持ってきたとしよう。 これを方眼紙の上で向きを変えずそのまま置いたなら、それぞれの図形は同じだけの重みで出現するはずだ。しかしこの図形を配置する時に、その並べ方の数が異なる。 図4に示す通り、図形VIIについてはただ1通り、図形IとV、VIについては2通り、他の図形については4通りある(これはコンピューターゲームで図形の向きを変化させた時に出現する配向の数に対応する)。 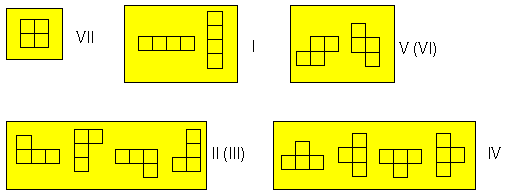
図4.図形I~VIIを配置する場合の数。図形VIは図形Vを、図形IIIは図形IIを裏返しにしたもので、それぞれ同じ結果となる。 出現確率の比は、この配置の数の比に等しい。 I : II : III : IV : V : VI : VII = 2 : 4 : 4 : 4 : 2 : 2 : 1 (2.2.1) だから、それぞれの出現確率は次のようになる:
|
この問題、みなさんはどのように考えられたでしょうか? そしてどちらの答えが正しいのでしょうか? ちなみに当化学教室の演習の時間に、大学3年生の方々約20人に解いてもらったところ、2人を除いて、ここで述べた「順次貼り合わせ」で解きました。
ここでこの問題に「化学平衡」を適用してみることにしましょう。 こうした問題に「化学平衡」を考えるには抵抗があるかもしれませんが、図形I~VIIをそれぞれエネルギー的には等価な何らかの「構造異性体」だと見ていただければよいでしょう。 ここでの議論は、反応のエントロピー的な面だけを取り出して考えるようなものです。
さて平衡として扱うとなると、「順次貼り合わせ」法での一方向の変化という設定に逆の方向の変化を取り入れ、それぞれの図形の間の相互変換を考えることになります。 この相互変換の形式としてはいろんなものが考えられるわけですが、ここでは図形IIとIVについて、中間に図形AやBを介した、下のようなプロセスを考えてみましょう。
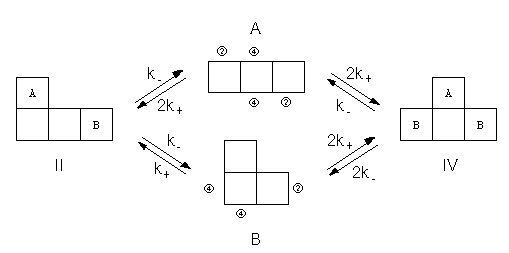
図5.図形A、B、II、IVの間の「化学平衡」。1つの場所に正方形が付く「反応速度定数」をk+、離れるのをk-とする。
この変化が釣り合っている時が平衡状態で、それは問題にしているすべての図形をでたらめに配置した状態に対応しているはずです。 ここで図5の平衡に「微視的可逆性の原理」を適用してみると、次の関係が成り立つことになります:
k- [II]e = 2k+ [A]e (3.1)
k- [II]e = k+ [B]e (3.2)
k- [IV]e = 2k+ [A]e (3.3)
2k- [IV]e = 2k+ [B]e (3.4)
この4つの関係式は独立ではありませんが、矛盾が起きないように係数が設定できています(例えば(3.1)~(3.3)式から(3.4)式が導ける)。この関係式から、
[A]e/[B]e = 1/2 (3.5)
[II]e/[IV]e = 1 (3.6)
同じようにして、他の図形についても平衡を考えてみると、それぞれの図形の比として
I : II : III : IV : V : VI : VII = 2 : 4 : 4 : 4 : 2 : 2 : 1 (3.7)
つまり2.2節で考えた、「配置の数え上げ」と同じ出現確率が得られます。
「順次貼り合わせ」と「配置の数え上げ」(あるいは化学平衡法)の結果が一致しなかったのはなぜでしょう?先の「順次貼り合わせ」に何か問題があったのでしょうか?
もし図3で考えた図形の構成法で、すべての場合が尽くされているのならば問題はないはずです。 しかし図3(図2も)で考えた図形の組み立てのプロセスには、欠けている経路があるのです。 たとえば図形IVについて、正方形を貼り合わせていく経路をすべて図示すると図6のようになります。
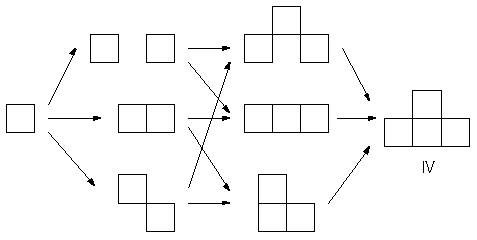
図6.正方形を順次配置して図形IVを生成する経路。中間に正方形同士が離れた図形を経由する場合がありうる。
この経路には、すべての正方形がつながっていない図形が3つ登場しますが、単に「でたらめに配置」していくだけなら、この図形も考慮しなければならないはずです。 図6にあるすべての経路を考慮すると、「順次貼り合わせ」法も、配向の数の勘定による方法、詳細釣り合いを用いた方法と同じ結果を与えます。 (なお、図2で考えた3つの正方形からできる図形A、Bの構成の場合には、つながっていない図形からの寄与が巧みに打ち消され、結果には影響を与えません。 それが、4つの正方形からなる図形I~VIIでは明るみに出てきたわけです。)
こうして見ると2.1節で見た「順次貼り合わせ」が、ナフタレンのスルホン化で見られるような「反応速度支配」の結果を与えたことになっていることがわかります。 2.1節の解法では、つながっていない図形を経る経路を無視していました。 このため、たとえば丸まった形の図形VIIの出現確率が高めに、そして広がった形の図形Iが低めに算定されています。 通常の反応速度論の言葉で言えば、つながっていない図形を経る経路の反応速度があまりに小さかった(ゼロだった)ために、最終生成物の比が、熱力学的な平衡から予測されるものとは必ずしも一致しなかったわけです。
なお「順次貼り合わせ」法によって、でたらめに配置したときの7つの図形の出現確率を求めるのは、一面で「しらみつぶし」法でもあります。 中間に出現するすべての図形(中間体)を考慮することになるからです。 このため「順次貼り合わせ」法では、探索すべき中間図形、経路の数は、図形が大きくなるにしたがって爆発的に増加していくことになります。 一方、配置の数の数え上げでは問題とする図形、化学平衡に基づく方法では問題とする図形の間を結ぶ何らかの経路を取り出せば、それぞれの図形の(相対的な)出現確率を算出することができます。 このことは計算機化学の世界では見逃せないことになるのですが、このお話はここではこれ以上取り上げません。
さて3章の図5で化学平衡を組み立てたとき、それぞれの過程の「速度定数」を「微視的可逆性」を念頭に対ごとに設定しました。それを下のように考えてみたらどうなるでしょう?
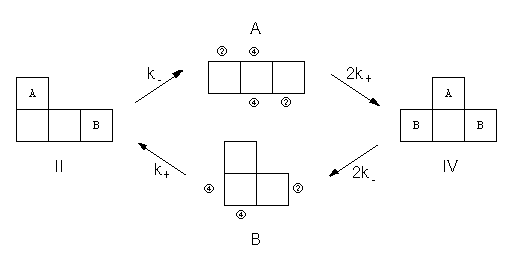
図7.図形A、B、II、IVの間の「化学平衡」のモデル。1つの場所に正方形が付く「反応速度定数」をk+、離れるのをk-とする。図形II→A→IV→B→IIの順に循環する反応モデル。
ここでは、II→A→IV→B→IIという風に、ぐるぐる回って変化することを前提に、「速度定数」を与えています。 こんなことをしたら、「詳細釣り合い」は成り立ちませんし、平衡についてもぜんぜん違う答えになってしまいそうです。 そこで、図7に従った時に、平衡状態でどういう関係が成り立つか調べてみると、次のようになります。
k- [II]e = k+ [B]e (5.1)
2k+[A]e = k- [II]e (5.2)
2k- [IV]e = 2k+ [A]e (5.3)
k+ [B]e = 2k- [IV]e (5.4)
この4つの式の中で矛盾はありません(たとえば(5.1)~(5.3)式から(5.4)式が導ける)。そして平衡の濃度比(出現確率の比)について
[A]e/[B]e = 1/2 (5.5)
[II]e/[IV]e = 2 (5.6)
という関係が得られ、(3.6)式で見た [II]e/[IV]e = 1 という関係は満たされません。 つまり先に見た「でたらめに配置」した場合の平衡分布から外れていて、いわば「反応速度支配」の結果になっているわけです。
ではここで図7の反応モデルで、IV→Bの「速度定数」を変更して、2k-をk-にしてみましょう。 すると上の(5.3)式と(5.4)式は次のように書き換えられます。
k- [IV]e = 2k+ [A]e (5.3')
k+ [B]e = k- [IV]e (5.4')
するとどうでしょう。 ここからは次のように(3.5)、(3.6)式と同じ関係式、「でたらめに配置」した分布が出てきます。
[A]e/[B]e = 1/2 (5.5')
[II]e/[IV]e = 1 (5.6')
平衡の関係を満たすだけなら、特に3章の図5のような設定にこだわる必要はないわけです。 詳細釣り合いの原理は、反応速度論の立場から化学平衡に対し一つの答えを与えてくれるものです。 けれども現象論的な速度論の立場による限り、それが唯一の答えというわけではないことは、心しておいてよいことです [1, 2]。
多成分系の反応と平衡は、しばしば「素反応さえ分かれば分かる」という扱いをされ、学生諸君にも多成分の反応と平衡に特有な問題の所在が理解されていないことが多いようです。 あるいはわれわれ自身、まだ気付いていない問題が秘められているかもしれません。 それは多成分系にまつわる問題が、一見自明に見える外観を持っているからであるように思います。 詳細釣り合いの原理も、何が問題かが明瞭に示されなければ、そのインパクトを十分には理解できないことでしょう。 歴史的に見ても化学者は、詳細釣り合いの原理をあえて問題とするほどのことでもない自明なものとしていた節があります [1]。 その意義をとらえ、その内実を原理にまで高めたのはオンサーガー(Onsager)でした[3]。
ここで取上げたのはコンピューターゲームに登場する図形の出現確率に取材した簡単な問題ではありますが、速度論的な、あるいは平衡論的な現象とそれを扱う手法の内実を顕著に示してくれる例ではないかと思います。 ここから学生諸君が多成分系の反応と平衡に対する問題意識を少しでも培ってくれることを期待します。