|
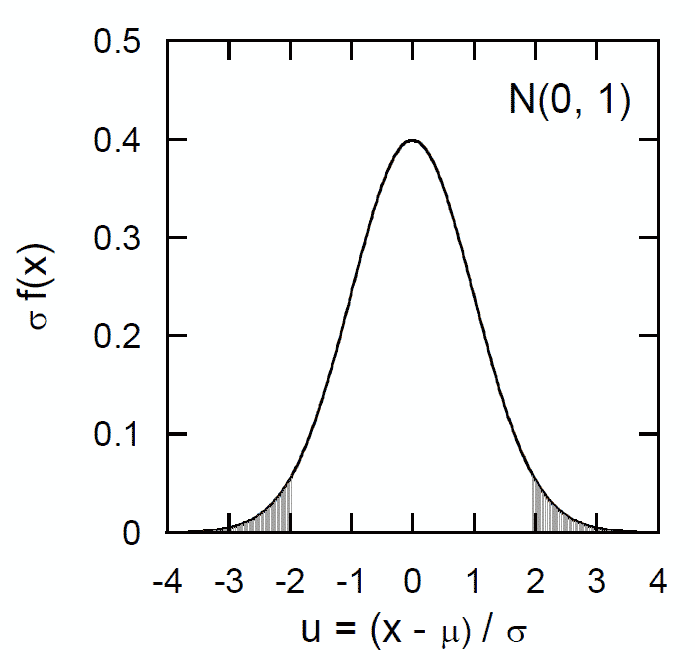
| 図1.正規分布 N(μ, σ2) を標準化した正規分布の確率密度。 図中影を付けた |u| > 1.96の部分の面積は 0.05。 |
得られたデータから何らかの結果を導くにあたって、 結果がどの程度もっともらしいかを評価する手続き・方法について、 あまり抽象的にならない形で簡単にまとめておきます。
現実の世界はさまざまな要素から構成されていて、 ある実験から得られたデータからただちに何らかの命題を証明することは困難です (たとえば同じ色だからといって、同じ物質とまではいえない)。 したがって多くの場合、「・・・と言えなくはない」といった形の反証の論理 logic of falsification が用いられ、 仮説検定と言われるものはそれを確率論の基礎の上に構成したものと言えます。
通常行われる仮説検定においては、 (1) 帰無仮説 H0 を立て 、 (2) その仮説が成り立つとして理論的結果(確率分布等)を導き、 (3) 実験結果が許容範囲内に収まらなければ(棄却域にあれば)H0を捨てる、 という手順を取ります。 ですから実験結果が許容範囲内に収まったからといって、 仮説が正しいとまでは言えない(棄却されない)ことに注意する必要があります。
棄却域の大きさ α を有意水準 significance level と呼びます。 有意水準は仮説 H0 が正しいにもかかわらず棄却する確率で、 この意味で危険率と呼ばれることもあります (基本「疑わしきは罰せず」の立場を取ります)。 通常の検定において棄却域は正負両端(両側)に α = 0.05になるように取ることが多いですが、 分野や用途によって棄却域の取り方はさまざまです。 たとえば平均値 μ 標準偏差 σ の正規分布 N(μ, σ2)では μ ± 1.96σ の範囲内にあれば 5 %の有意水準で棄却されません。 この ± 1.96σ といった範囲を示す値を限界値 critical value と呼び、 あからさまに有意水準の値ではなく、± σ の範囲であれば棄却しないなど、 限界値で有意水準を定める場合もしばしばあります。
「推定」という作業は、実験結果を満たすように仮説を想定する作業と言えます。 典型的には実験である物質の物性値 x について xa という結果が得られたとき、 x = xa が満たされるという仮説が有意水準 α で成立する範囲を求め、 「その物質の物性値 x は xa ± δであった」という形で結論を下します。 最小2乗法は、こうした物性値(あるいは分布を特徴づけるパラメータ)を推定するのに用いられる代表的な手法になります。
仮説から導き出される理論的な結果にはさまざまなものが考えられます。 実験の標準偏差があらかじめ分かっている場合には比較的単純ですが、 実験の標準偏差があらかじめ分かっていない場合には t 分布や χ2 分布、F 分布などに基づく検定が行われます。 こうした統計処理には多くの演算処理が必要とされ、かつては膨大な数表が利用されました。 今日では Excel などの表計算ソフトでたいていの作業はこなせ、 さらに進んだ統計の専用パッケージとしては SAS や SPSS、STATISCA(有料)、R(無料)などが著名です。
酸化還元滴定でシュウ酸マンガン(MnC2O4·2H2O)とされる試料 0.2305 g 中に含まれるシュウ酸の質量が H2C2O4 として0.1151 g であったとしましょう。
酸化還元滴定で定めるシュウ酸量の分布が正規分布に従い、 標準偏差が 0.20 %であるとあらかじめ分かっているものとして、 この結果からどのような結論を導けるか考えましょう。
仮説検定の手順に従い、仮説 H0 として 「試料は純粋なシュウ酸マンガンである」 を立てます。 すると、各物質の式量と与えられた標準偏差から 「試料 0.2305 g 中に含まれるシュウ酸含量の実験結果は平均 0.1159 g で標準偏差 0.23 mg の正規分布に従う」 という理論的結果が得られます。 ここで有意水準 5 %の棄却域として 0.1154 g 以下 0.1164 g 以上を取りましょう (正規分布では ±1.96 σ の範囲内に 95 %が収まる)。 実験結果は棄却域にあるので仮説 H0 は棄却され、 「有意水準 5 %で『試料は純粋なシュウ酸マンガンである』とは言えない」 という結論を得ます。
「推定」の立場からは、たとえば仮説として「試料は純度 q のシュウ酸マンガンである」を立て、 「試料 0.2305 g 中に含まれるシュウ酸含量の実験結果は平均 0.1159q g で標準偏差 0.23q mgの正規分布に従う」 という理論的結果を得て、 実験結果 0.1151 gについて
(0.1159q - 0.00046q) < 0.1151 < (0.1159q + 0.00046q)
を満たすように q の範囲を0.989 < q < 0.997と定め、 「試料のシュウ酸マンガンの純度は (99.3 ± 0.4) %である(有意水準5 %)」 といった結論を与えることになります。 化学分析においては、こうした記述がむしろふつうです。 なお推定の立場では、たとえば仮説の中の「シュウ酸マンガンである」ことについての判断が背景に押しやられてしまうことがあるので注意が必要になります。
未知の対象について何らかの実験を繰り返し行った際、 多くの場合、その平均や分散などについて分かっていません (というか分からないので実験する)。 こうした場合、実験で求めた平均値がある仮説を満たすかどうかの判定には t 検定がよく用いられます。
平均 \(\mu\)、標準偏差 \(\sigma\) の正規分布に従う結果が得られると期待される実験を \(N\) 回行って、 データ \(x_i ~(i = 1 \ldots N)\) を得て、 その標本平均が \(\bar{x}\)、標本標準偏差が \(s\) であったとしましょう。 この時 \(z = (\bar{x} - \mu)/(s/\sqrt{N} )\) は自由度 \(N - 1\) の t 分布に従うとみなせることが知られています。 自由度 \(\phi\) の t 分布の平均は0、分散は\(\phi/(\phi - 2)\) で与えられ、 自由度 \(\phi\) が大きい場合、平均 0 分散 1 の標準正規分布に漸近します。
貯金箱にいっぱい入った百円玉から適当に25 個取り出して重さを量り、その平均が 4.781 g、標本標準偏差が 0.031 gであったとしましょう。 この貯金箱に入っている百円玉の重さの平均が「通貨の単位及び貨幣の発行等に関する法律施行令」による量目 4.8 g と一致するかどうかを考えてみます。 帰無仮説 H0 として「貯金箱に入っている百円玉の重さの平均が 4.8 gに等しい」を立てます。 標準偏差が分かっていないので \(z = (\bar{x} - \mu)/(s/\sqrt{N})\) を求めればこれは t 分布に従うと見なせます(理論的帰結)。 t 分布の数表を参照すると、有意水準 5 %の棄却域としては \(z\) が -2.064 以下 2.064 以上を取ればよいことになります 。 すると \((4.781 - 4.8)/(0.031/\sqrt{25}) = -3.06\) であり、 有意水準 5 %で「貯金箱に入っている百円玉の重さの平均が 4.8 gに等しい」という仮説 H0 は棄却されます。
|
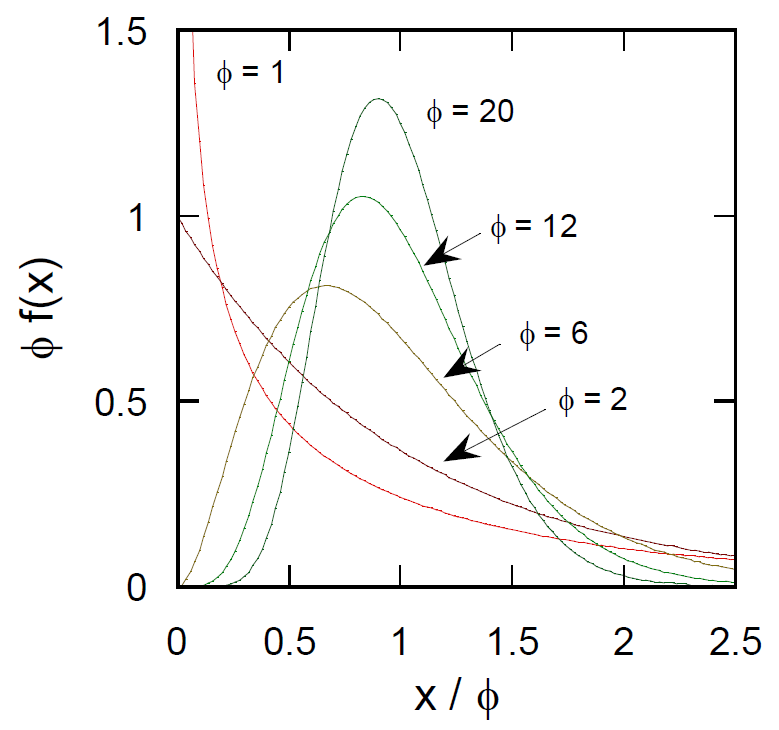
| 図3.種々の自由度 \(\phi\) に対するカイ2乗分布の確率分布(\(\phi\)でスケールしてある)。 自由度が大きくなるにつれゆっくり正規分布 N(\(\phi\), 2\(\phi\))に漸近する |
分散 \(\sigma^2\) を与える実験を \(N\) 回行った標本分散が \(s^2\) であったとすると \(v = s^2/\sigma^2\) は自由度 \(N - 1\) のカイ2乗分布に従うと見なせます。 自由度 \(\phi\) のカイ2乗分布の平均は \(\phi\) 、分散は \(2\phi\) で与えられます。
事象の出現頻度を理論(仮説)と実験で比較し仮説の当否を判定する際にカイ2乗χ2 検定がよく用いられます。 典型的な適合度検定 goodness of fit test では \(N\) 回の実験の実験結果を \(k\) 個の級に分け、 それぞれの級のデータの出現回数 \(r_i\) と理論(仮説)から予想される期待回数 \(e_i\) から次のような値 \(\chi^2\) を求めます:
\[ \chi^2 = \sum_i {\frac{(r_i - e_i)^2}{e_i}} \]
\(N\) が大きい時、\(\chi^2\) は自由度 \(k - 1\) のカイ2乗分布に従うことが知られており、 \(\chi^2\) の値が大きい時仮説を棄却することになります。 もし期待回数 \(e_i\) が測定値から割り出される値(標本平均など)を \(r\) 個含む時は、自由度は \(k - r - 1\) になります。
「川沿いに男女が並んで座る時、左右どちらになるかは等確率である」という仮説 H0 を検討するため、 鴨川沿いの 25 組の男女について調べ、男が右側に座っていたのが17組であったとしましょう。 \(\chi^2\) を求めると \((8 - 12.5)^2/12.5 + (17 - 12.5)^2/12.5 = 3.24\)です。 級の数は左右の 2 ですから自由度は1であり、自由度 1 で有意水準 5 %となる \(\chi^2\) の値 は 3.84... なので 5 %の有意水準で仮説 H0 は棄却されず 「有意水準5 %で、男女が並んで座る時、左右どちらになるかは等確率であるといえなくもない」 という結論を得ます。
2つの統計集団の比較には F 検定がよく用いられます。 F 検定は統計集団の分散に注目した手法で、 分散分析(ANOVA。analysis of variance)の主要なツールでもあります。
自由度 \(\phi_1\)、\(\phi_2\) のカイ2乗分布に従う変数\(v_1\)、\(v_2\) を考えると両者の比 \(x = (v_1/\phi_1)/(v_2/\phi_2)\)は 自由度 \((\phi_1, \phi_2)\) の F 分布に従います。 自由度 \((\phi_1, \phi_2)\) の F 分布の平均は \(\phi_1\) によらず \(\phi_2/(\phi_2 - 2)\)です。 F 分布の累積分布が \(P\) になる \(x\) の値を \(F(\phi_1, \phi_2; P)\) と表記して F 分布に関する数表が整備されています(いまでは使われることはないでしょうが・・・)。 \(F(\phi_1, \phi_2; P)\) と \(F(\phi_2, \phi_1; P)\) の間には
\[ F(\phi_1, \phi_2; P) = \frac{1}{F(\phi_2, \phi_1; 1-P)} \]
の関係が成立します。
正規分布 N(\(\mu_1\), \(\sigma_1^2\))、N(\(\mu_2\), \(\sigma_2^2\)) に従う母集団から、 大きさ \(N_1\)、\(N_2\) の標本を得て、 それぞれの標本分散が \(s_1^2\)、\(s_2^2\) であったとします。 この時 \(u = (s_1^2/s_2^2)/(\sigma_1^2/\sigma_2^2)\) は自由度 \((N_1 - 1, N_2 - 1)\) の \(F\) 分布に従います。 つまり標本分散の比 \(s_1^2/s_2^2\) が自由度 \((N_1 - 1, N_2 - 1)\) の \(F\) 分布で極めて低い確率でしか実現されないものなら、 \(\sigma_1^2 = \sigma_2^2\) とは見なせないことになるわけです。
合金中の亜鉛の組成 \(x\) %を重量分析と容量分析で決定する実験を K大学の優秀な学生たちが行い、 重量分析は 88 件で \(x\) の標本分散 \(s_\mrm{W}^2 = 3.453\)、容量分析は 23 件で標本分散 \(s_\mrm{V}^2 = 2.357\) であったといいます。 この結果から重量分析と容量分析による分析値の分散に差があるかどうかを考えてみましょう。 「重量分析と容量分析の分散は等しい」という仮説 H0 が正しいならば、 重量分析と容量分析の標本分散の比は自由度 (87, 22) の F 分布に従います。 F(87, 22; 0.975) = 2.102 であり 、実験で求められた標本分散の比 3.453/2.357 = 1.465 はこれより小さく 「有意水準5 %で重量分析と容量分析の分散は等しいと言えなくはない」 ということになります。
なお丁寧に考えるなら、\(s_\mrm{W}^2/s_\mrm{V}^2\) に関し \(x\) の小さい側に存在する棄却域 \(x\) < F(87, 22; 0.025) = 0.545 に入るかどうかの判断もする必要がありますが \(s_\mrm{W}^2/s_\mrm{V}^2 \gt 1\) なのでこのチェックをあえて行っていません。 もし\(s_\mrm{W}^2 \lt s_\mrm{V}^2\) であったなら、 通常 \(s_\mrm{V}^2/s_\mrm{W}^2\) について F(22, 87; 0.975) = 1.835 より大きいかどうかで判断する形を取ります (分子分母を入れ替える判断を加えることで、両側の棄却域を考慮したことになる)。 F(22, 87; 0.975) = 1/ F(87, 22; 0.025)に注意します。 こういう手法はかつて、数表を利用していた時代には当然でした(数表記載の数値がほぼ半分になる)。 けれども Excel 等の使用が当たり前になった今の時代には、かえって面倒かもしれません。
測定値の中に他の値からかけ離れたもの (外れ値 outlier と呼びます。outlier は恐竜の化石と一緒に空き缶が出てくるようなもの)がある時、 それを除外して取り扱います。 外れ値を判定する際の明確な基準は難しい問題です。 概ね標本標準偏差の2倍以上外れたものを外れ値とすることが多いでしょう。
データ量が多い時には、上位・下位の25 %を省くといった手法がとられることがあります。 データ量があまり多くない時にはスミルノフ Smirnov(-グラブスGrubbs)検定といった手法も用いられますが、 正規分布するという前提が満たされる保証はなく、積極的に採用する理由に乏しいと思います。