|
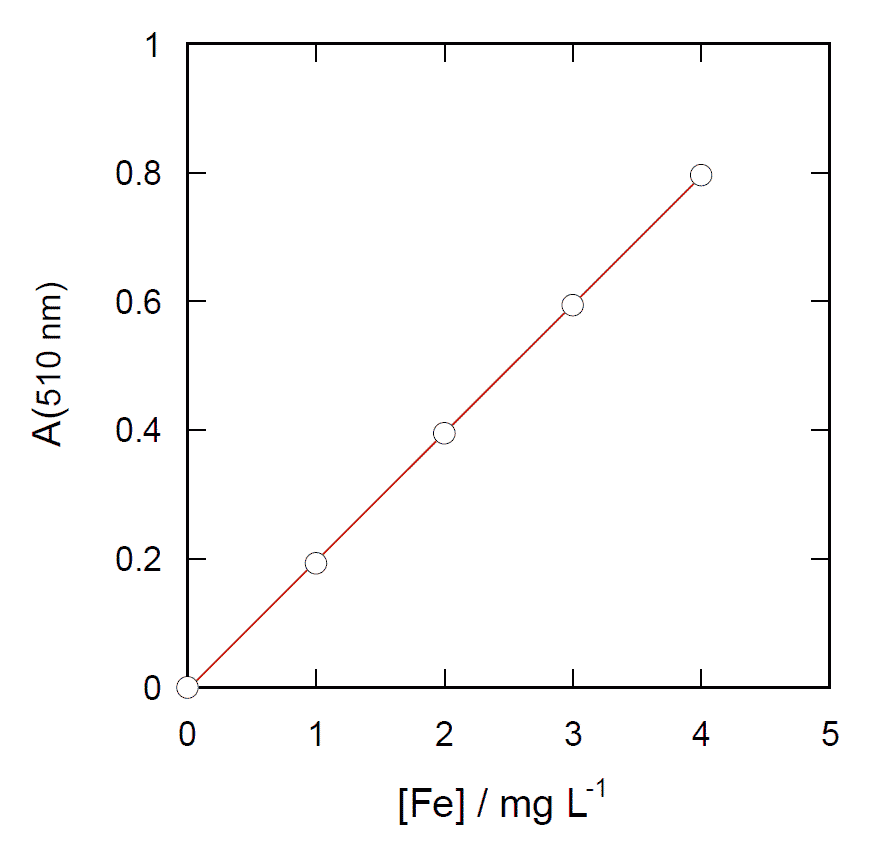
| 図 1. 鉄フェナントロリン錯体の検量線。 510 nm における吸光度 |
光吸収を用いた濃度測定は、 非破壊的な分析法として頻用されます。 この項については、以前行った解説も参照していただけるといいでしょう。
可視・紫外領域の光(概ね 200 nm~800 nm)の吸収は分子における様々な電子状態間の遷移によって起きます。 こうした遷移の起こる波長、遷移の強度などは分子に固有のものなので、 これを測定する事によってその分子の濃度を調べることが可能となります。 入射光強度 \(I_\mrm{i} (\lambda)\) と出射光強度 \(I_\mrm{o} (\lambda)\) の比を透過度 transmittance といい、その常用対数をとって符号を変えたものを、吸光度 \(A(\lambda)\) と呼びます。
\begin{equation} A(\lambda) = -\log_{10} \frac{I_\mrm{o} (\lambda)}{I_\mrm{i} (\lambda)} \label{eq:absorbance} \end{equation}
モル濃度 \(c\)、光路の長さ \(\ell\) の試料溶液に波長 \(\lambda\) の光を通したとき、 吸光度に対して、次の関係が成立します (ランベルト-ベール Lambert-Beer(あるいは ブーゲ-ベール Bouguer-Beer)の法則)。
\begin{equation} A(\lambda) = \epsilon(\lambda) c \ell \label{eq:lbrule} \end{equation}
ここで \(\epsilon(\lambda)\) はモル吸光係数と呼ばれる量で、 分子に固有の定数になります (単位としては、使用する濃度単位 mol/L、光路長 cm の関係で、 たいてい mol-1 L cm-1 が用いられます)。
\eqref{eq:lbrule} 式より、 光路長の定まった光学セル(生化関係の人は”キュベット” と呼ぶことが多いです)で、 濃度既知の溶液を用い、ある波長でのモル吸光係数を決めておけば、 吸光度を測ることによって、試料溶液中の濃度を決定することができます。
可視・紫外分光光度計は、入射光強度と出射光強度を測定し、 透過率あるいは吸光度に換算して表示または記録する装置でということになります。 光源としては紫外領域では重水素ランプ、可視領域ではタングステンランプを使ったものが、よく用いられています。 最近、長寿命のキセノンフラッシュランプを用いた分光光度計も普及してきました。
ランベルト-ベールの法則は、光を吸収する分子の濃度が高いと成り立たなくなります。 また使用する分光光度計によって、測定可能な吸光度の大きさ(通常 2 程度)、 吸光係数は異なります (吸光係数は物質固有のものですが、 スリット幅など、測定機器の装置特性・設定条件によって、実効的な吸光係数は少し違ってきます)。
このため定量に当たっては、いくつかの濃度で光吸収の測定を行います。 そして横軸に濃度、縦軸に吸光度をプロットして、直線性がどの程度なりたつか、 またその勾配(吸光係数)がいくらかを求めます。 この濃度-吸光度の関係を示したグラフを、検量線と呼びます。 検量線が精密に決まっておれば、ランベルト-ベールの法則に従わない非直線性をしめす領域でも定量が可能ではあるのですが、 誤差が大きくなることが多く、溶液を希釈するなりして、非直線性の領域は避けたほうが無難です。
光学セルに埃がついていたり、溶液中にごみが浮いていたりすると、期待する吸光度は得られません。 測定にあたっては、光学セルの光の透過する面は清浄にしておかなければなりません。 光学セルごとにセル自体の吸収、散乱が異なるので、異なるセルを用いて吸光度を測定するときは、 光学セル自体の吸収、散乱をあらかじめ補正する必要があります。 また浮遊物があるときには溶液をろ過するといった操作も必要になります。 こうした光吸収測定の前段階が、精確なデータを得る上で最も重要ですが、 異なる波長の吸光度の差を取ったりすることが、 有効な場合もあります。
原理的には、測定波長は注目する物質が吸収する光の波長ならどの波長でもよいわけですが、 吸光度が急激に変化する波長は避けるべきです。 分光光度計ではある波長幅(通常 2 nm程度。スリット幅と呼ばれるもの)の光を積算して光の透過率を求め、 その対数をとって吸光度を表示する仕組みになっています。 ですからその波長幅で透過率が急激に変化すると、 分光光度計が表示する吸光度はその波長幅での平均値とは一致しなくなります。 測定波長として最大吸収波長をとるのは、感度が高いことはもとより、吸光度の変化が小さい点で好ましいのです。 また異なる分光光度計を使用する際には、機種間の設定の違いに留意する必要があります。
実際に分光光度計のセンサーが感じるのは、光の強度(透過率)であって、吸光度ではありません。 試料物質による光吸収が強くて、透過光の強度が微弱だと、 測定の精度は悪くなります。 このため、通常、分光光度計は吸光度が 1 を越えないようにして測定を行います。 この一方吸収が小さくて、ほとんど検知できなくても測定精度は悪くなります。 このあたりの事情を単純化したモデルで考えてみましょう。
透過率 \(T\) を \(\Delta T\)(> 0)の不確かさで知ることのできる分光光度計があったとします。 このとき、吸光度の不確かさは \(\Delta T/T ~(\ll 1)\) に比例します。
\begin{equation} \ln (T \pm \Delta T) \approx \ln T \pm \Delta T/T \label{eq:transmerr} \end{equation}
ですから吸光度 \(A\) の相対誤差は次式で表されます( \(T = 10^{-A}\) に注意)。
\begin{equation} \frac{\Delta A}{A} \propto \Delta T \frac{10^A}{A} \label{eq:twy} \end{equation}
したがって吸光度の相対誤差は、透過率の誤差 \(\Delta T\) が \(T\) によらず一定ならば、 図 2 のように変化し(トワイマン-ローシャンTwyman-Lothianの曲線)、
\begin{equation} A = -\log \mrm{e} = 0.434 \label{eq:twy1} \end{equation}
のとき、つまり吸光度が 0.434 のとき相対誤差は最小になります。 つまり、吸光光度計で濃度を決定する際には、吸光度が 0.4 前後の値が望ましいことになります。