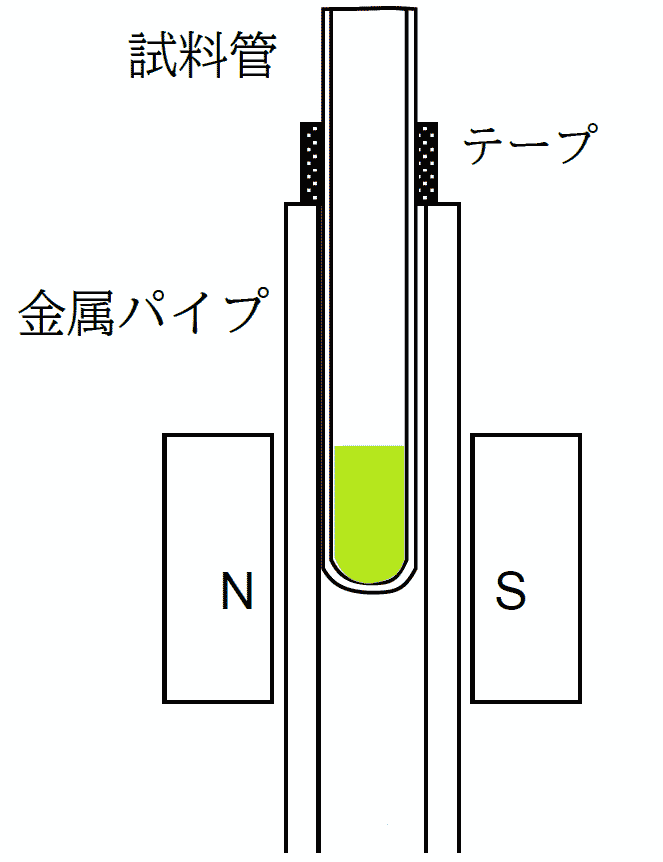
|
| 図 1. 磁気天秤 MSB-MKI の試料部分の模式図。対向する磁石の間に非磁性の金属管が配置され、 金属管中に試料管を挿入して磁石に働く力を測定。 |
物質の示すさまざまな性質の中で、磁性は原子・分子の内部構造を反映するものとして古くから研究されてきました。 ここでは磁化率と、磁気天秤を用いた磁化率の測定法について紹介します。 また磁化率については、どのような単位系をとるか、あるいは \(E\mbox{-}H\) 対応をとるか \(E\mbox{-}B\) 対応をとるかでさまざまな流儀があるので、 電磁気に関わる諸概念の構成・単位についても簡単に触れておきます。
物体を磁場の中におくと、作用する磁場に応じて磁気分極 \(M\) が生じ、 多くの場合、磁気分極 \(M\) は磁場 \(H\) に比例するものとみなせます （\(\mu_0\) は真空の透磁率(磁気定数) \(4 \pi \x 10^{-7}\) H m-1。 ここでは SI 単位に基づいて \(E\mbox{-}H\) 対応の観点から述べます。 単位や \(E\mbox{-}H\) 対応、 \(E\mbox{-}B\) 対応については後述）。
\begin{equation} M = \mu_0 \chi H \label{eq:magnetization} \end{equation}
磁気分極 magnetic polarization は磁化 magnetization とも呼ばれます。 磁荷 magnetic charge と紛らわしいので、ここでは電気分極と対応させて磁気分極と呼ぶことにします。 また \(E\mbox{-}B\) 対応の立場からは、\(M = \chi H\) で磁化率が定義されますが、 後述するように、この \(M\) はここでの磁気分極とは異なる物理量です。 なお真空の透磁率の値は 2019 年の SI の定義変更により、厳密には \(4 \pi \x 10^{-7}\) H m-1 ではなくなりましたが、 実際上は変更がないものとして取り扱って問題ありません。
この比例係数 \(\chi\) を磁化率と呼びます。 後述の質量磁化率と区別するため、しばしば \(\chi\) は体積磁化率 \(\chi_V\) と呼ばれます。 磁化率が負の場合を反磁性（diamagnetism。水や有機液体などで典型的には \(\chi\) ～ -10-6）、 正であまり大きくない場合（～ 0.001）を常磁性（paramagnetism）、 正で大きい場合（～ 1000）を強磁性（ferromagnetism）と呼びます。 強磁性の場合には外部から磁場を与えなくとも磁化が存在し（「磁石」）、 磁化率は単純な挙動を示しません。 通常、反磁性、常磁性に関わって磁化率が論じられます。
磁気分極 \(M\) は物体中の分子の持つ磁気双極子モーメントの密度に相当し、 測定される領域における試料の密度に比例します。 したがって、物質の個性を表す上で質量磁化率 \(\chi_\mrm{g}\) あるいはモル磁化率 \(\chi_\mrm{mol}\) がよく用いられます （\(\rho\) は密度、\(FW\) はモル質量）：
\begin{equation} \chi_\mrm{g} = \chi_V/\rho, ~~~ \chi_\mrm{mol} = FW \chi_\mrm{g} \label{eq:gmsuscep} \end{equation}
質量磁化率、モル磁化率はそれぞれ比容、モル体積の次元を持ちます。
|
|
| 図 1. 磁気天秤 MSB-MKI の試料部分の模式図。対向する磁石の間に非磁性の金属管が配置され、 金属管中に試料管を挿入して磁石に働く力を測定。 |
学生実験での磁化率の測定には Sherwood Scientific 社製の磁気天秤 MSB-MKI を使用します。 この磁気天秤は不均一な磁場中に試料を置いた時に働く力を測定し、 標準物質の場合と比較することで試料の磁化率を得るものです。
装置の試料をセットする部分は図１のような構成になっていて、 対向する永久磁石の間に非磁性の金属パイプが配置されています。 金属パイプ中に試料管に詰めたサンプルを挿入すると、試料が常磁性であれば磁場の強い中心部に引き込むように、 反磁性であれば外に押し出すように力を受けます。 この力を MSB-MKI は磁石に取りつけた金属線のねじれ具合で検出するように設計されています。 磁化率が 1 より十分小さければ、 試料に働く力は、生じた磁気分極 \(M\) に比例し、 磁気分極 \(M\) は磁化率 \(\chi\)（\(= \chi_V\)）に比例すると見なせます。 したがって磁化率のよく知られた標準物質と未知試料とに働く力の比を測定することで、 未知試料の磁化率を知ることができるわけです。
学生実験では標準物質としてトリス(エチレンジアミン)ニッケルチオ硫酸塩 [Ni(en)3]S2O3（en = エチレンジアミンC2N2H8）を用います。 [Ni(en)3]S2O3 の質量磁化率 \(\chi_\mrm{g}\) は室温で 11.0 × 10-6 cm3 g-1（CGS emu）、 室温付近 t °C の質量磁化率は次式で表されることが知られています （N. F. Curtis, J. Chem. Soc. 1961, 3147。 CGS emu については、後段の解説参照）。
\begin{equation} \chi_\mrm{g} = \frac{2759 }{\mrm{t} + 230} \x 10^{-6}~\mrm{cm^3 ~ g^{-1} ~ (CGS~ emu)} \label{eq:stdchi} \end{equation}
標準物質として、入手が容易なモール塩 (NH4)2Fe(SO4)2·6H2O （室温付近で \(\chi_\mrm{g}\) = 32.3 × 10-6 cm3 g-1 (CGS emu)） を使ってもいいでしょう。 けれども均一な粉末をえるのが難しく、 トリス(エチレンジアミン)ニッケルチオ硫酸塩の方が安定な結果を与えるようです。
測定に先立って、まず磁気天秤の周りに工具など強磁性のもの等がないか、 立ち位置によって磁気天秤の示す値が変わったりしないか（変化する場合には静電気の影響が疑われます）を確認します。 以前、机の引き出しに入っていたペンチのために、測定値が不安定になっていたことがありました。
|
| 図 2. 試料管。テープの位置がずれないように |
試料管には外径 4 mm の肉薄のガラス管を 7 cm 程度に切って、 一端をバーナーで閉じたものが用意してあります （磁気天秤付属の正規品の試料管は高すぎる！）。
図 2 のように試料管の底面から 45 mm 程度のところにテープ（ビニルテープで可）を巻きます。 分厚く巻く必要はありません。 図 1 に見るように、 テープの位置で試料管が磁気天秤に挿入される深さ、 磁気天秤中の磁石対の間のどの位置に試料が来るかが決まります。 この挿入位置で磁気天秤の感じる力は大きく変化するので、 このテープの位置を重要です。
実験ではもっぱら粉末試料の磁化率を測定します。 粒度が荒いと、均一に詰まってくれず、 また結晶の異方性の影響があって安定な結果を得られません。
乳鉢の使用も考えられますが、 使用する試料がもろい無機塩類なので、 試料を素焼きの板の上で、スパチュラなどですり潰すので十分です。 なおこの時、金属製のスパチュラを使用すると、特に反磁性の物質の場合、 影響が出るかもしれないので、プラスチック製のスパチュラを使うのがよいでしょう。
空の試料管の重さを精密天秤ではかり、 試料管にすり潰して細粉にした試料を、 試料管に高さが 3 cm ぐらいまで詰めます （高さ 1 cm ぐらいでも測れないことはありませんが、安定な結果をえるには多い方がよいようです）。 詰める時は紙の上で、試料管の口にスパチュラなどで掃き寄せてもいいですが、 マイクロピペッターのチップの先端を切ったものを漏斗にするのが簡単です。 試料管に試料の細粉を入れ終えたら、 最後、均一に詰まるようにコツコツと机の上で叩いておきます（タッピング）。
こうして試料を詰め終わったら、 詰めた試料のおもさを精密天秤ではかり、 試料の高さを 0.1 mm まで物差しで読み取ります。
試料管はガラスでできていて、空の状態では反磁性を示し、磁力は負。 試料管を押し出す方向の力が働きます。 そこに測定試料の粉末を入れた時の磁力の変化が、試料に由来する磁力になります。 同一の試料管を用いて、標準物質と試料を測定するのが望ましいのですが、 テープの位置を揃えておけば大きな問題にはならないようです。 磁化率の測定手順は次のようになります。
\begin{equation} \chi_\mrm{g} = \frac{(L/w) (R - R_x)}{(L_0 / w_0) (R_0 - R_x)} \x 11.0 \x 10^{-6} ~ \mrm{cm^3 ~ g^{-1}} \label{eq:calcchi} \end{equation}
電磁気を取り扱う際に用いられる概念やその単位には、 電場・磁場に関する理解のスタンス、 あるいは着目する事象や歴史によって、今日でも混乱が見られます。 特に磁気分極（磁化）や磁化率をめぐっては、伝統的に CGS emu単位系（CGS 電磁単位系）が用いられていて、 SI 単位（MKSA単位系）とは単位の呼称も大きさもちがいます。 また同じ CGS emu あるいは SI 単位を用いていても、 流儀によって同じ言葉で異なる物理量を指すことがあるので注意が必要です（いわゆる \(E\mbox{-}H\) 対応と \(E\mbox{-}B\) 対応の問題）。 ここでは化学で普通に使われる \(E\mbox{-}H\) 対応の立場から、 まず磁場に関する概念を SI 単位に基づいて整理した後、 CGS emu 系との対応をまとめておきます。
JIS では、国際量体系（ISQ）にならって概念・用語の整理が行われ、
磁場ではなく「磁界」が採用され、
単に「磁場」と呼んでいた \(H\) が「磁界強度」とされるなど、
ぼくのようなオールドタイマーは、いささかためらっています
（JIS Z 8000-6「量及び単位 — 第6部：電磁気」。昔は理学系は「磁場」、工学系は「磁界」と住みわけがあったんですが・・・）。
ここでは取りあえず、昔ながらのことばづかいで行きます。
なお化学の立場からは、今井功「電磁気学を考える」サイエンス社 1990 は、
一読をお薦めしたい本です。
SI における磁荷 \(Q_\mrm{m}\) の単位は Wb（ウェーバー）で、\(Q_\mrm{m}\) の磁荷からは \(Q_\mrm{m}\) /Wb 本の磁力線が出ていると考え磁束と呼びます。 磁束密度 \(B\) はある面を過ぎる磁力線の密度で単位は T（テスラ）です（T = Wb m-2 です。 等方的な環境であれば \(Q_\mrm{m}\) の磁荷から距離 \(r\) 離れた点での磁束密度 \(B\) は \(Q_\mrm{m}/4 \pi r^2\)）。
磁力線にはゴムひものように張力が働き、 また互いに反発しあうと考えることができます。 磁場 \(H\) は磁力線１本当たりに働く力を表わすものと考えることができ、 磁力線に沿って単位面積当たり \(HB\) の張力、 また磁力線間には単位面積当たり \(HB/2\) の等方的な斥力が働くと見なせます （マクスウェル応力と呼ばれ、単位は Pa です。 ここで \(HB\) は応力テンソルを表しますが、 単なる磁場と磁束密度の掛け算と考えておいてもらってよいでしょう）。 真空中で \(H\) は \(B\) に比例し、\(H = B/\mu_0\) と表されます。 ここで \(\mu_0\) は真空の透磁率（磁気定数）です。 また磁場は単位体積当たり \(HB/2\) の電磁エネルギーを持ちます （ここで \(HB\) は内積です。エネルギー密度と圧力は同じ次元を持つことに注意します。J m-3 = Pa）。
電磁気に関する単位を考える上でポイントになるのは、 電荷 \(Q\) と磁荷 \(Q_\mrm{m}\) の積が作用の次元（プランク定数と同じ）を持つことでしょう。 SI 単位では C Wb = J s になります（電荷は磁荷と正準共役の関係）。 電位の単位 V（ボルト）に対し磁位の単位は A（アンペア）であり（C = A s と同様に Wb = V s であることに注意）、 電場の単位 V m-1 に対し磁場 \(H\) の単位は A m-1 になります。 また真空中の磁束密度を磁場で割った、真空の透磁率（磁気定数）\(\mu_0\) の単位は、 先にも触れたように Wb m-2/(A m-1) = H / m になります（H はインダクタンスの単位でヘンリー。V s /A）。
|
| 図 2. 物体中でも磁力線の本数は変わらないので、 法線方向の磁束密度 \(B\) は変化しないが、磁場 \(H\) は磁気分極のため変化する。 |
真空中で物体（絶縁体とします）を磁場の中におくと、 作用する磁場に応じて磁気分極 \(M\) が生じます。 真空と物体の境界面に垂直方向で考えると、 磁束密度 \(B\) は連続ですが、磁気分極の存在のため磁場 \(H\) は不連続になります。 この関係を数式では、次のように表せます。
\begin{equation} B = \mu_0 H + M, ~~ H = (B - M)/\mu_0 \label{eq:bandhm} \end{equation}
さて先にも述べたように多くの場合磁気分極 \(M\) は磁場 \(H\) に比例するものとみなせます。
\begin{equation} M = \chi \mu_0 H, ~~ B = (1 + \chi) \mu_0 H = \mu H \label{eq:bandhm1} \end{equation}
先に述べたように比例係数 \(\chi\) は磁化率と呼び、 \(\mu\) を透磁率 permeability、 \(\mu/\mu_0 (= 1 + \chi)\) を比透磁率と呼びます。 常磁性体では磁気分極は磁束密度の方向に沿って生じるので、 常磁性体内の磁場は真空中より小さくなり、 マクスウェル応力によって常磁性体の境界面は単位面積当たり \(MB/2\) の力で真空中に引っ張られることになります。
\(MB = (\chi \mu_0/\mu) B^2 = [\chi/(1 + \chi)]B^2\) より、 磁化率 \(\chi\) が小さければ、働く力は磁化率に比例すると見なせます。
\(E\mbox{-}B\) 対応の立場では、 誘起される磁場を磁気分極 \(M\) で表して \(B = \mu_0(H+ M)\) とし、 \(M = \mu_0 H\) という形で磁化率を定義します。 この文脈では分子は「分子電流」によって磁気モーメントを持ち、 それが配向することで磁気分極が生じるという立場をとります。 \(E\mbox{-}B\) 対応では、\(M\) を「磁化」と呼び、 \(E\mbox{-}H\) 対応での磁気分極を\(\mu_0 M\) と表記するのが普通です。 \(E\mbox{-}B\) 対応では \(E\mbox{-}H\) 対応とは、 磁気分極（磁化）\(M\)・磁気モーメントが異なる物理量を表すことになるので特に注意が必要です。
磁気モーメントの単位は \(E\mbox{-}H\) 対応では Wb m ですが、\(E\mbox{-}B\) 対応では A m2 = J/T をとるのが普通で、 ”電流モーメント” のようなものになります。 そこで \(E\mbox{-}H\) 対応の磁気モーメントのことを、 \(E\mbox{-}B\) 対応では普通「磁気双極子モーメント」と呼んで区別します。 なお \(E\mbox{-}B\) 対応の立場であっても、\(M = \chi H/\mu_0\) で磁化率を定義する流派、 逆に \(E\mbox{-}H\) 対応の立場で \(M = \chi H\) として磁化率を定義する流派もあります。 この時には磁化率は無次元量（単位 1 の物理量）ではなく、 透磁率と同じ次元を持つ物理量となります。 こうした混乱があるので、教科書類を参照するときは、定義によく注意する必要があります。
伝統的に用いられてきた CGS 電磁単位系（CGS emu）では、 長さの単位を cm、質量の単位を g に取るとともに、 電磁気に関する新たな基本単位を設けず、真空の透磁率 \(\mu_0\) が 1 になるように単位系を構成しています。 また磁荷 \(Q_\mrm{m}\) から \(4 \pi Q_\mrm{m}\) 本の磁力線（磁束）が出ていると考えることで、 球対称の系における取り扱いを容易にしています（特に点磁荷の間の相互作用は簡単な形になります）。 このため磁束密度と磁場との関係には次式のように \(4\pi\) という因子が必要になります。
\begin{equation} B_\mrm{CGS} = H_\mrm{CGS} + 4 \pi M_\mrm{CGS} = (1 + 4\pi \chi_\mrm{CGS}) H_\mrm{CGS} \label{eq:cgbh} \end{equation}
このためSI系における磁化率はCGS電磁単位系の磁化率の \(4 \pi\) 倍になります。
\begin{equation} \chi_\mrm{SI} = 4\pi \chi_\mrm{CGS} \label{eq:cgchi} \end{equation}
CGS 電磁単位系での磁束密度の単位はG（ガウス）、磁場の単位はOe（エルステッド）です。 ただし真空の透磁率 \(\mu_0\) を 1 に取っている関係で、CGS 電磁単位系での磁束密度と磁場は同じ次元を持つ物理量となり （真空中の問題では数値まで一致する）、G と Oe の混同がしばしば見受けられます。 しかしこれは距離の単位の「光年」を不用意に使用して10年に10光年を加えるといった無意味な演算を招くのと同様、避けるべきでしょう。
元来、真空中で距離 \(r\) 離れた電流 \(I_1\)、\(I_2\) の間に働く単位長さあたりの力を \(2I_1 I_2 / r\) の形で表現しようとするところから構想されたので CGS 電磁単位系と呼ばれます。 SI で\(\mu_0 = 4 \pi \x 10^{-7}\) H m-1 としているので、磁束密度の単位 G と T の間には、1 T = 10000 G という切りのよい関係が成り立ちます。 なお CGS 系においても磁荷 \(Q_\mrm{m}\) から磁束 \(Q_\mrm{m}\) が生じるとする流儀があり、 有理化 CGS と呼ばれますが、磁気化学の分野ではあまり一般的ではありません。