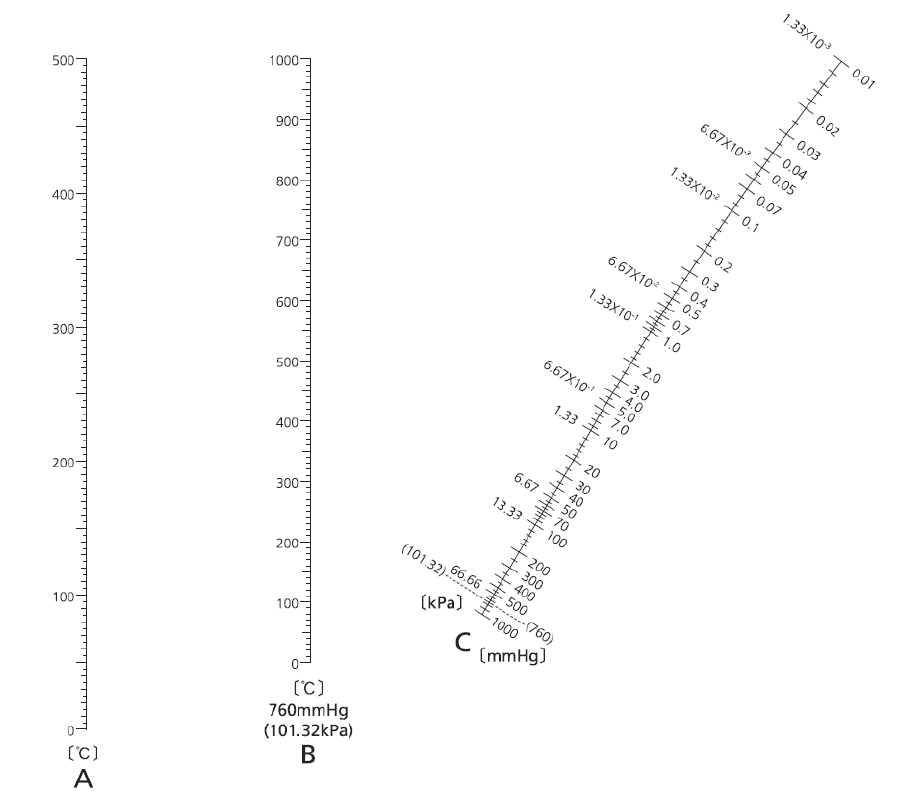
図 1. 減圧下の沸点を推算するノモグラフ (東京化成のカタログから孫引き。元はScience of Petroleum Vol. II, 1281 (1938))
液体の蒸気圧に関わって、 よく知られたアントワーヌの式とそのパラメーター、 減圧時の沸点の推算についてまとめておきます。
液体の蒸気圧 \(P\) の温度 \(T\) 依存性は、およそ 1 kPa~200 kPa程度の圧力範囲では、 次のアントワーヌ Antoine の式で精度よく表現できることが知られています (1 bar = 100 kPa = 0.98692 atm = 750.06 Torr。1 Torrは1 mmHg)。
\begin{equation} \log_{10} (P / \mrm{bar}) = A - \frac{B}{(T/ \mrm{K}) + C} \label{eq:antoine} \end{equation}
以下には種々の液体について、 通常沸点(蒸気圧が 1 atm になる温度)付近の蒸気圧データに対して定められたアントワーヌ式のパラメータをまとめておきます (NIST の webbook から)。 文献やハンドブック等を参照する時は、注目する温度領域、圧力・温度の単位の取り方などによって、 アントワーヌ式のパラメータの値が異なることに注意する必要があります(常用対数ではなく、自然対数を取っている場合もあります)。 NIST で集約された通常沸点 tb の値も付記しておきます。
なお 1 atm 付近は良いのですが、1 kPa 以下、200 kPa 以上にまで外挿すると、 とんでもない結果になることがあるので要注意です (そもそも気液の臨界現象は再現できません)。
| 液体 | A | B | C / K | tb / °C |
|---|---|---|---|---|
| acetone | 4.42448 | 1312.253 | -32.445 | 56.1 ±0.3 |
| acetonitrile | 4.27873 | 1355.374 | -37.853 | 81.6 ±0.3 |
| aniline | 4.34541 | 1661.858 | -74.048 | 184 ±2 |
| benzene | 4.72583 | 1660.652 | -1.461 | 80.1 ±0.3 |
| carbon tetrachloride | 4.02291 | 1221.781 | -45.739 | 76.6 ±0.1 |
| chloroform | 4.20772 | 1233.129 | -40.953 | 61.1 ±0.2 |
| cyclohexane | 3.17125 | 780.637 | -107.29 | 80.7 ±0.2 |
| dichloromethane | 3.97323 | 1016.865 | -56.623 | 40 ±1 |
| ethanol | 5.24677 | 1598.673 | -46.424 | 78.3 ±0.2 |
| ethyl acetate | 4.22809 | 1245.702 | -55.189 | 77.0 ±0.2 |
| ethyl ether | 4.02200 | 1062.640 | -44.93 | 34.5 ±0.2 |
| hexane | 4.00266 | 1171.530 | -48.784 | 68.7 ±0.3 |
| methanol | 5.20409 | 1581.341 | -33.50 | 64.6 ±0.3 |
| octane | 4.04867 | 1355.126 | -63.633 | 125.5 ±0.5 |
| 1-propanol | 4.87601 | 1441.629 | -74.299 | 97.1 ±0.5 |
| 2-propanol | 4.86100 | 1357.427 | -75.814 | 82.3 ±0.4 |
| sulfur dioxide | 3.48586 | 668.225 | -72.252 | -8.9* |
| tetrahydrofuran | 4.12118 | 1202.942 | -46.818 | 66 ±1 |
| toluene | 4.07827 | 1343.943 | -53.773 | 110.6 ±0.2 |
| water | 4.65430 | 1435.264 | -64.848 | 100.02 ±0.04 |
熱化学的標準状態の取り方が「25 °C、1 bar」になった関係で、 以前、1 atm における沸点を「標準沸点 standard boiling point」としていたのを、 「通常沸点 normal boiling point」と呼んでいます。 今も 1 atm での沸点を標準沸点としているケースは多く、 その一方で律儀に 1 bar での沸点を標準沸点としている場合もあるので、注意が必要です。 なお表中 * を付けた二酸化イオウの沸点の値は、 アントワーヌの式から計算したものです。
古くから分子の成り立ちと蒸気圧、沸点の関係は検討されており、 特に有機化合物については多くの推算法が提案されています (液体物性の推算法については、 B.E. Poling, J.M. Prausnitz, J.P. O'Connell , "The Properties of Gases and Liquids," 5th, McGraw-Hill 2001. ISBN 9780070116825 が ”バイブル” といっても良いでしょう)。 ここでは減圧蒸留に関わって、1 atm での通常沸点から減圧下の沸点を推算する、 ”実践的” なノモグラフ nomograph (計算図表)を図 1 に紹介しておきます(通常の非会合性液体用のものです)。
たとえば通常沸点が 220 °C の物質を、分解を防ぐために 100 °C で蒸留したい場合、 図 1 の B 軸上の 220 °C の点と A 軸上の 100 °C の点を結ぶ直線を引き、 C 軸の交点約 2.1 kPa (16 Torr) まで減圧すればよいと推定するわけです。 なおweb上には、 シグマ-アルドリッチ(現メルク)のサイトのように、 このような推算を対話的に行うページもあります (「nomograph」で検索をかけてもヒットするようです)。