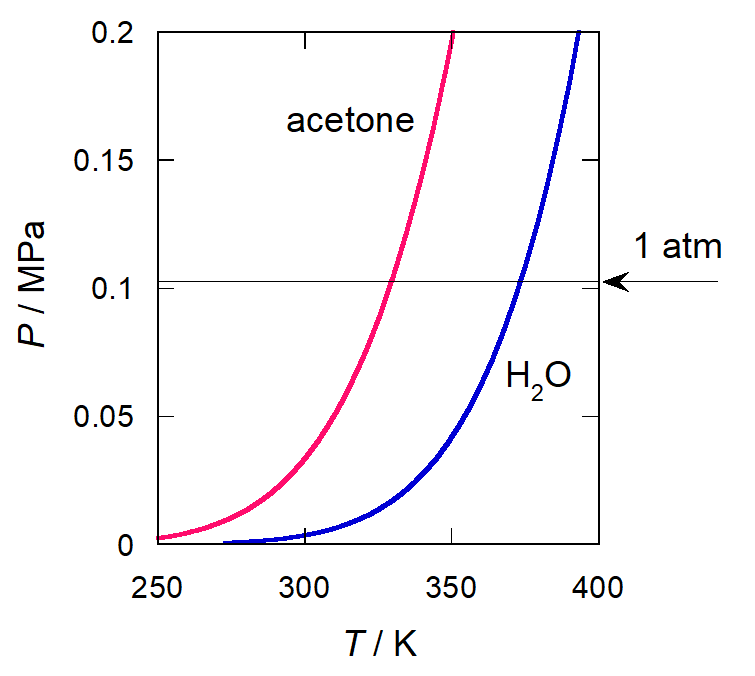
図 1. アセトン (赤) と水 (青) の蒸気圧の温度依存性
熱力学では物質のさまざまな釣り合い、平衡が問題とされます。 固体に比べて気体・液体は、比較的容易に平衡に達し、 また異方性がないので取り扱いが簡単です。 まずは高校までに学んだ理想気体の状態方程式や蒸気圧曲線といった話題から始めて、 物質の状態を記述する熱力学的な物理量を眺めてみましょう。 そして多くの変数からなる世界の様相に触れてみましょう。
物質の気体・液体の圧力 P は温度 T と密度(モル濃度)c を指定すると決まります (体積 V、物質量を n とすると、c = n/V)。 あるいは気体・液体の状態を決めるのはこの P、T、c の3変数で、 それぞれはある関数関係 P(T, c) で結ばれているというわけです。 こうした関係式を状態方程式 equation of state と呼び、 物質を特徴づける基本的な関係式です。 十分希薄な気体では、気体の種類によらず、 次の理想気体の状態方程式が成り立つことはよくご存じのことでしょう。
\begin{equation} P = cRT \label{eq:idg} \end{equation}
密度 c は単位体積あたりの物質量で SI 単位では mol m-3。 温度 T は熱力学的温度で SI 単位は K(ケルビン)、圧力 P の SI 単位は Pa(パスカル N m-2)です。 そして R は気体定数で、8.3144626... J mol-1 K-1 (SI では定義量で、 ボルツマン定数 k = 1.380649 × 10-23 J K-1 に アボガドロ定数 6.02214076 × 1023 mol-1 を掛けたもの)です。 成分が複数ある場合には、 密度を各成分の密度 ci(i = 1, 2, …)の和で置き換えればよいだけです。
\begin{equation} P = \sum_i c_i RT \label{eq:idgmc} \end{equation}
大気圧は 1 atm = 101.325 kPa ですから、25 °C で考えると、 理想気体の密度はおよそ 40 mol m-3、モル体積で考えると 0.025 m3 mol-1、 25 L mol-1 ぐらいということになります。 1 気圧の空気の質量密度がおよそ 1.2 kg m-3 で(モル質量およそ 0.03 kg mol-1 相当)、 水の密度(およそ 1000 kg m-3 = 1.0 g cm-3)の 1/1000 ぐらいなのは、記憶しておいてよいことです (あるいは液体が蒸発すると 1000 倍ぐらいに膨張する)。
理想気体の状態方程式は、 熱力学温度の定義式と考えることもできます。
\begin{equation} T = P/cR \label{eq:tdefid} \end{equation}
また気体の各成分の濃度を、各成分の分圧 Pi の形で表示することも行われます。
\begin{equation} P_i = c_i RT \label{eq:ppre} \end{equation}
先に見た状態方程式で、圧力は温度と密度の関数でしたが、 熱力学では、こうした多変数関数を取り扱うことになります。 特に何らかの熱力学量の変化・摂動にともなう、他の熱力学量の変化・応答を、 問題にすることがしばしばです。 数学の授業では、より厳密な取り扱いを学ぶことになるでしょうが、 ここでは化学熱力学で大切な、多変数関数の微分とその変数変換について、 直観的、実用的な立場から、眺めておきます。 簡単のため、2変数関数 \(z(x, y)\) について考え、 \(z(x, y)\) は十分滑らかな関数だとします。
空気の圧力を変化させるという同じ操作にも、 体積を一定にして温度を変えることもできれば、 温度を一定にして容器の体積を変える、 あるいは外部から空気を送り込むということもできます。 多変数関数の微分では、ある条件を付けて変化量を調べることになり、 微分も偏微分という形を取ります。
関数 \(z(x, y)\) について、ある条件イの下で \(x\) を変化させた時の \(z\) の偏微分係数(偏導関数)を、 次の極限をとる形で考えます。
\begin{equation} \pdifA{z}{x}{イ} = \lim_{(h, h') \to 0} {\frac{z(x + h, y + h') - z(x, y)}{h}} \label{eq:pdifdef} \end{equation}
条件イには種々のものが考えられますが、\(y\) を一定(\(h' = 0\))とする条件がよく用いられます。 条件の記法としては、\(x\) を変化させるときに一定にする量を記すことが多く、 また文脈から明白な場合、しばしば省略されることがあります。
偏微分係数の満たすべき性質として、 次の偏微分の順序交換についての要件は大切です。
\begin{equation} \lpar{ \pdif{}{y}\pdifA{z}{x}{y}}_x = \lpar{ \pdif{}{x}\pdifA{z}{y}{x}}_y \label{eq:pdifex} \end{equation}
ですから、\(\partial z/\partial x = x + y\) の時に \(\partial z/\partial y = y\) であってはならないわけです。 化学熱力学の世界では、 「圧力 P 一定で温度 T を変え、引き続き T 一定で P を変えた時の体積 V の応答」と 「 T 一定で P を変え、引き続き P 一定で T を変えた時の体積 V の応答」が等しいという主張というわけです。 当たり前のようですが、液体の圧縮に気を取られている人と、 膨張に気を取られている人が出会うと、時としてこのあたりの整合性が問題になります。 また後ほどマクスウェルの関係式で出会うことになります。
合成関数の微分の公式 \(\rmd y/\rmd x = (\rmd y/\rmd z) (\rmd z/\rmd x) \) については、 よくご存じのことでしょう。 偏微分の場合には、いわば面上の微分を考えるので、いささか厄介です。
\((x, y) \) 平面の原点 \((0, 0)\) の近傍で \(z(x, y)\) が \(x, y\) についての 1 次式で表せると考えます(ある平面で近似すると思えばよいでしょう)。
\begin{equation} z = z_x x + z_y y \label{eq:dz1} \end{equation}
ここで \((x, y)\) という変数の組を \((p, q)\) という変数の組に変換します(簡単のため、原点は動かさないとします)。 \(x(p, q)\)、\(y(p, q)\) も同様に \(p, q\) についての 1 次式で表せるとすると、次のように書けます。
\begin{equation} \begin{array} {l } x &=& x_p p + x_q q \\ y &=& y_p p + y_q q \end{array} \label{eq:dz2} \end{equation}
したがって式 \eqref{eq:dz1} は次のようになります。
\begin{equation} z = (z_x x_p + z_y y_p) p + (z_x x_q + z_y y_q) q = z_p p + z_q q \label{eq:dz3} \end{equation}
この \(p\) についての係数に注目すると、 偏微分係数について次の変換公式が成立します(連鎖律)。
\begin{equation} \pdifA{z}{p}{q} = \pdifA{z}{x}{y} \pdifA{x}{p}{q} + \pdifA{z}{y}{x} \pdifA{y}{p}{q} \label{eq:pdchain} \end{equation}
ここからさまざまな関係式が得られます。 式 \eqref{eq:pdchain} で、 \(p = z, q = y\) だとすると、\((\partial y/\partial z)_y = 0\) ですから
\begin{equation} 1 = \pdifA{z}{x}{y} \pdifA{x}{z}{y}, ~~~ \pdifA{z}{x}{y} = 1/ \pdifA{x}{z}{y} \label{eq:pdinv} \end{equation}
偏微分する条件が同じなら、 常微分の時の \((\rmd y/\rmd x) (\rmd x/\rmd y) = 1\) と同じで、 あたかも分数の演算のように扱えるわけです。
さて式 \eqref{eq:pdchain} で、 \(p = x\) だとすると、\((\partial x/\partial x)_q = 1\) ですから、 次式が成り立ちます。
\begin{equation} \pdifA{z}{x}{q} = \pdifA{z}{x}{y} + \pdifA{z}{y}{x} \pdifA{y}{x}{q} \label{eq:pdchain1} \end{equation}
たとえば圧力一定の条件での熱容量と、体積一定での熱容量との差に相当するものが、 この右辺第2項で評価されるわけです。 またさらに式 \eqref{eq:pdchain1} で、\(q = z\) だとすると次の関係が成り立ちます。
\begin{eqnarray} 0 = \pdifA{z}{x}{y} + \pdifA{z}{y}{x} \pdifA{y}{x}{z} \label{eq:pdchain2a} \end{eqnarray}
式 \eqref{eq:pdinv} に注意すると、この式は次の形にまとめられます。
\begin{eqnarray} \pdifA{z}{x}{y} \pdifA{x}{y}{z} \pdifA{y}{z}{x} = -1 \label{eq:pdchain2} \end{eqnarray}
高校までに学んだ常微分の式であれば 1 になるところですが、 -1 になることに注意してください。 多変数関数では、「どのように微分するか」というのがポイントになっています。 またそれは、後でも触れる断熱圧縮率や等温圧縮率のように、熱力学的な過程で、 「どのような条件で操作するか」がポイントであることでもあります。
\[ \lpar{ \begin {array}{c} x\\ y \end {array} } = \lpar{ \begin {array}{c c} x_p & x_q \\ y_p & y_q \end {array} } \lpar{ \begin {array}{c} p\\ q \end {array} } \]
のように記述していった方が、もっと見通しがよいでしょうが、 あまりに抽象的になりそうな気がしています。物質を知るには、叩いたり、温めたりして、どのような変化・応答が見られるかを調べてみます。 ここでは圧縮、膨張にかかわる量を見てみることにします。
| 物質 | κT/GPa-1 |
|---|---|
| エタノール | 1.11 |
| トルエン | 0.91 |
| 水 | 0.45 |
| ポリスチレン | 0.25 |
| 水銀 | 0.040 |
| 塩化ナトリウム | 0.042 |
| アルミニウム | 0.0133 |
| ガラス(パイレックス) | 0.027 |
| 黄銅(真鍮) | 0.0089 |
| 鉄(軟) | 0.0059 |
| 石英ガラス | 0.0027 |
| ダイアモンド | 0.0016 |
圧力をかけた時、どの程度密度が変動するかを表すのが圧縮率です。 等温圧縮率(定温圧縮率) \(\kappa_T\) では、温度 \(T\) 一定で、圧力 \(P\) をかけた時に、どれくらい密度 \(c\) が大きくなるかに注目します。
\begin{equation} \kappa_T = \frac{1}{c} \pdifA{c}{P}{T} \label{eq:comp} \end{equation}
表 1 に、常温常圧での、種々の物質の等温圧縮率をまとめました。 普段目にする、液体・固体は少々の圧力では圧縮されず、 数気圧(1 atm ≈ 105 Pa)かけても、せいぜい 1/10000 程度の密度の変化が起きる程度です。 この一方、表には示していませんが、気体の等温圧縮率は、物質の種類によらず式 \eqref{eq:idg} から \(1/P\) になり、 大気圧ではおよそ 10 MPa-1 で1万倍以上。 圧力を下げれば、差はさらに大きくなり、 気体と液体・固体では非常に大きな差があることが分かります。
けれどもよく見ると、 通常の液体(ガソリン等)の等温圧縮率はおよそ 1 GPa-1 (= 10-9 Pa-1) 程度で、 固体ではこれより1ケタ以上圧縮率は小さく、 多くの金属では 0.01 GPa-1 以下ぐらいになっています。 材料として考えると、変形にどれだけの圧力(応力)が必要かに注目することが多く、 しばしば固体では圧縮率の逆数、体積弾性率 bulk modulus が用いられます。 材料力学などで学ぶことになるでしょうが、ヤング率は体積弾性率と深い関係にあります。
なお音速などにも関わって重要な断熱圧縮率は、外部との熱の出入りを断った条件下での圧縮率で、 一般に等温圧縮率より小さくなります(後ほどに触れます)。
\begin{equation} \kappa_T = \frac{V}{n} \pdifA{n/V}{P}{T, n} = \frac{V}{n} \pdifA{n/V}{V}{T, n} \pdifA{V}{P}{T, n} = -\frac{1}{V} \pdifA{V}{P}{T, n} \label{eq:comp2} \end{equation}
| 物質 | α/kK-1 |
|---|---|
| エタノール | 1.08 |
| トルエン | 1.06 |
| 水 | 0.21 |
| ポリスチレン | 0.45 |
| 水銀 | 0.181 |
| アルミニウム | 0.069 |
| 黄銅(真鍮) | 0.06 |
| 鉄 | 0.035 |
| ガラス(パイレックス) | 0.008 |
| 岩塩 | 0.11 |
| 石英ガラス | 0.0005 |
| ダイアモンド | 0.004 |
温度を変化させた時、どの程度密度が変動するかを表すのが体膨張係数(熱膨張率あるいは単に膨張率とも呼ばれます)です。 体膨張係数 \(\alpha\) では、圧力 \(P\) 一定で、 温度 \(T\) を上げた時に、どれくらい密度 \(c\) が変化するかを表すもので、 通常、温度を上げると密度は小さくなるので、下式のように符号を逆にします。
\begin{equation} \alpha = -\frac{1}{c} \pdifA{c}{T}{P} \label{eq:expan} \end{equation}
表 2 に、常温常圧での、種々の物質の体膨張係数をまとめました。 表には示していませんが、気体の体膨張係数は、物質の種類によらず式 \eqref{eq:idg} から \(1/T\) になり、 室温、約 300 K 付近で約 3 kK-1(= 3 × 10-3 K-1)程度です。 等温圧縮率では、気体と液体・固体でけた違いに大きな差があったことを考えると、 体膨張係数での差異はあまり大きくありません。
多くの有機液体の体膨張係数はおよそ 1 kK-1 程度で、 1 K 温度を上げると 1/1000 程度の密度の低下が起きます。 固体ではおおむねこれより 1 ケタ小さくなりますが、 体膨張係数は物質の個性に強く依存します。 たとえば水では 4 °C 以下で負になりますし (水は 4 °C で密度が極大)、 インバー®合金(FeNi36)のようにほぼ熱膨張を示さない合金も知られています。
密度一定で温度を変化させた時の圧力の変動を表すのが、圧力係数(温度圧力係数とも)です。 圧力係数 β は次式で表され、 式 \eqref{eq:pdchain2a} に注意すると、 膨張率 \(\alpha\) を等温圧縮率 κT で割ったものになります。
\begin{equation} \beta = \pdifA{P}{T}{c} = -\pdifA{P}{c}{T} \pdifA{c}{T}{P} = \alpha / \kappa_T \label{eq:pcoeff} \end{equation}
アルコールなど通常目に触れる液体の圧力係数はおよそ 1 MPa K-1(= 106 Pa K-1)程度で、 密閉した容器に入れて温度を 1 K 上げると 10 気圧程度の圧力上昇が起きることになります。 固体の場合は、 1 K で 100 気圧程度になることもありますが、 一方気体であれば圧力係数は \(P/T\) (\( = Rc\) )ですから、 常温常圧では 1 K 上げて、0.03 気圧程度の圧力増加にとどまります。
圧力係数は、機械材料などで、熱応力の問題と関わって重要な量です。 化学熱力学では、圧縮率や膨張率の陰に隠れて、あまり表立って取り上げられることが少ないですが、 物質の成り立ちを考える上で重要な量です。
液体の沸騰、気体の凝縮や蒸気圧については、高校までにある程度、学んできたところでしょう。 混合物の分留などの話題は後回しにして、 ここでは純物質の気体・液体の沸騰・凝縮について見ておきます。
圧力一定で液体を加熱し、温度を上げていくと、沸騰が起きて気体になります。 また逆に気体の温度を下げていくと、凝縮が起きて液体になります。 沸騰が起きる温度を沸点(凝縮の場合は露点)と呼び、 純物質では沸点と露点は一致し、この時の圧力を蒸気圧と呼びます。
液体の蒸気圧は温度の上昇とともに、図 1 に示すように指数関数的に増加していきます。 通常の液体の蒸気圧 \(P\) の温度 \(T\) 依存性は、およそ 1 kPa~200 kPa 程度の圧力範囲では、 次のアントワーヌ Antoine の式で精度よく表現できることが知られています
\begin{equation} \log_{10} (P / \mrm{bar}) = A - \frac{B}{(T/ \mrm{K}) + C} \label{eq:antoine} \end{equation}
ここで \(A,~ B,~ C\) は物質によるパラメータです(1 bar = 100 kPa = 0.98692 atm)。 アントワーヌの式は蒸留操作の設計などでよく用いられます。 ただし与えられたパラメータの有効範囲外に外挿して使用すると、大きな誤りにつながることがあるので、 有効範囲には注意が必要です。 またアントワーヌの式には、常用対数ではなく自然対数を用いたり、温度・圧力の単位がちがったり(°C や Torr (= mmHg) を用いたりするなど)、 さまざまな表式があるので注意します。
蒸気圧が 1 atm の時の温度を通常沸点 normal boiling point と呼び、 水はほぼ 100 °C です (元来 100 °C になるように摂氏目盛りは作られたのですが、 現在使用されている温度目盛り ITS-90 では 99.974 °C です)。 なお以前は 1 atm の時の温度を「標準沸点」と呼んでいましたが、 標準状態を 1 bar(= 100 kPa)とする立場から、 蒸気圧が 1 bar の時の温度を標準沸点と呼ぶようになり、 今も混乱があるので注意が必要です。
温度を下げると蒸気圧は急速に低下します。 水の蒸気圧は 100 °C から 60 °C まで下げると、1 気圧から 0.2 気圧、 さらに 20 °C にすると 0.02 気圧ぐらいになります。 密度を見ると、液体の水の密度は 100 °C では 960 kg/m3 が 20 °C で 1000 kg/m3 と 4 % ほど増える一方、 水蒸気の密度は蒸気圧の低下を強く反映して、理想気体の状態方程式 \eqref{eq:idg} から予想されるように、 0.6 kg/m3 ぐらいから 0.02 kg/m3 まで大幅に減少します。 このように温度を下げると、蒸気と液体の密度の差が拡大していくのですが、 逆に温度を上げると両者の差は縮小していきます。 そして最後には差がなくなり、気液の分離、 沸騰・凝縮が起きなくなります。
気液分離に関わって、実際にどのような過程が進行するのか、 容量が 10 L の小型のプロパンガスのボンベに、プロパンを詰めることを例に考えてみましょう (実際には余裕を見て 12 L ぐらいですが、簡単のため 10 L とします。 また市販のプロパンガスにはブタンなども入っていますが、プロパン 100 % とします)。 最初、ボンベを真空に引いておいて、 ここに温度 20 °C の状態でプロパンを詰めていくとします。 プロパンを入れるにつれ圧力は上がっていきますが、圧力が 0.8 MPa を超えるぐらい、0.2 kg も詰めたところで、 圧力の増加が止まります(ここでは ”現場” で使われるゲージ圧、大気圧を 0 とした圧力ではなく、 真空を 0 とした「絶対圧」をとります)。 プロパンの 20 °C での蒸気圧は 0.84 MPa(8.3 atm)で、 蒸気の質量密度は 18 kg m-3 です。 液化が始まったのです。 ここからさらにプロパンを詰めていくと、圧力はそのままで、 液体プロパンの量が増えていきます。 そして 5 kg 入れたところでさらにプロパンを入れようとすると、 圧力をもっとかけないといけなくなります。 蒸気がなくなって全量が液体プロパンになったわけです (プロパンの 20 °C での飽和液体密度は 500.1 kg m-3)。 ここに後 0.1 kg プロパンを余分に詰めようとすると、 5 MPa ぐらいの圧力が必要になります (液体の圧縮率は気体よりケタ違いに低かったですね)。 プロパンの容器の充填圧力(FP)はせいぜい 2 MPa ですから(耐圧は余裕を見て 3 MPa ぐらい)、 無茶をするとボンベが破裂しかねません。
図 2b は、こうした温度一定で密度を変化させた時の圧力の変化の様子を、 いくつかの温度についてまとめたものです。 20 °C の曲線を質量密度 ρ = 0 からたどっていくと、 上で見たように、ρ = 18 kg m-3 まで圧力が増加して行き、 そこから液化が始まって密度を増加させても(内容物は不均一ですが、総体としての密度を考えます)圧力は 0.84 MPa で一定となり、 密度 ρ = 500 kg m-3 で液化が完了し、 そこから急速な圧力増加が起き、 ρ = 510 kg m-3 では圧力 P = 4.6 MPa になります(危ない)。 さてこれが夏場で温度が 40 °C まで上がったら (法的には 40 °C 以下に保つことになっています)、 密度 ρ = 30 kg m-3(圧力 P = 1.37 MPa) で液化が始まり、 ρ = 467 kg m-3 で液化が完了し、 そこから急速な圧力増加が起きます。 20 °C の時同様に 5 kg のプロパンを入れようとしたら 11.8 MPa まで圧力を上げることになります(危ない!)。 5.1 kg まで入れようとしたら 16.5 MPa です(危ない!!)。 こうしたことを見越して、5 kg 用のボンベは余裕をみて大きめに作られています (容量 12 L であれば 40 °C でも蒸気相があり、圧力は 1.37 MPa 止まり)。
さてさらに温度を上げていくと、蒸気相の密度は上がり、液相の密度は下がり、 97 °C で蒸気と液体の密度は ρ = 220 kg m-3 で同じになります。 つまりこれ以上の温度では、液化・蒸発が起きなくなり、 気体と液体の区別がなくなるわけです。 この気液の分離が起きなくなる温度を臨界温度 Tc、 その時の圧力を臨界圧力 Pc、密度を臨界密度 cc、 この状態を臨界点と呼びます。 こうした臨界温度、臨界圧力、臨界密度(臨界モル体積を採用することも多い)を臨界定数と呼び、 それぞれの物質を特徴づけるパラメータとなっています。 表 3 にはいくつかの物質について、通常沸点(1 気圧における沸点)と臨界パラメータをまとめました。
| 物質 | 化学式 | Tb/K | Tc/K | Pc/MPa | cc/mol L-1 |
|---|---|---|---|---|---|
| ヘリウム | He | 4.2 | 5.2 | 0.23 | 17.5 |
| アルゴン | Ar | 87.3 | 150.7 | 4.86 | 13.3 |
| 窒素 | N2 | 77.4 | 126.2 | 3.39 | 11.1 |
| 酸素 | O2 | 90.2 | 154.6 | 5.04 | 13.7 |
| 二酸化炭素 | CO2 | 194.6 | 304.1 | 7.38 | 10.6 |
| アンモニア | NH3 | 239.8 | 405.6 | 11.36 | 14.3 |
| 水 | H2O | 373.1 | 647.1 | 22.06 | 17.9 |
| 水銀 | Hg | 629.8 | 1764 | 167 | 23.3 |
| メタン | CH4 | 111.6 | 190.6 | 4.60 | 10.1 |
| プロパン | C3H8 | 231.0 | 369.9 | 4.25 | 5.0 |
| ブタン | C4H10 | 272.6 | 425.2 | 3.79 | 3.9 |
| トリフルオロメタン | CHF3 | 191.1 | 299.0 | 4.82 | 7.5 |
これらの物質の中で、窒素、酸素などは 19 世紀後半ごろまでは「永久気体」と呼ばれ、 液化できないと考えられていましたが、低温技術と物理化学の進歩の中、液化が可能であることが明らかになったものです。 またメタン、プロパンなど有機化合物などの臨界圧力はせいぜい 10 MPa ぐらいまでですが、 水は 22 MPa、水銀は 167 MPa と、無機化合物にはかなり高い臨界圧力を示すものがあります。 なお表中、トリフルオロメタンは HFC23(R23 とも)と呼ばれる、エアコンに最近よく用いられている冷媒です。
密度が高くなるに従い、気体は理想気体の挙動からはずれてきます。 室温付近、通常の気体では希薄な状態から密度を上げるに従い、圧力は理想気体からの予想より小さくなります。 次のビリアル状態方程式は、低密度での圧力・温度の挙動を記述するのに用いられます。
\begin{equation} Z = \frac{P}{cRT} = 1 + B(T) c + C(T) c^2 + \cdots \label{eq:vireq} \end{equation}
ここで \(B(T)\) を第 2 ビリアル係数、\(C(T)\) を第 3 ビリアル係数などと呼び、温度 \(T\) の関数です。 また \(Z = P/cRT\) を圧縮率因子と呼びます。 図 3 にはいくつかの気体について、第 2 ビリアル係数の温度依存性を示しました。 室温付近で気体の第 2 ビリアル係数はたいてい負で、分子間の引力的相互作用が大きい気体ほど負で大きな値を取り、 また温度依存性も大きくなります。 第 2 ビリアル係数は温度を上げるに従って大きくなり、0 になる温度をボイル温度 (ボイルは人名で R. Boyle (1627 - 1691)。ボイルの法則のボイルです)と呼びます。 ヘリウムは室温付近で正の第 2 ビリアル係数を持ちますが、 極低温では負になります(ボイル温度は 28 K、-245 °C ぐらい)。 ビリアル係数は分子間相互作用との関連が付きやすく(大きい分配関数の密度展開と呼ばれる手法に対応します)、 理論的な研究も多く積み重ねられてきています。
常温常圧で、気体の密度がおよそ 40 mol m-3 ですから、 窒素や酸素のように第 2 ビリアル係数が -10 cm3 mol-1 程度ですと、 理想気体と考えた時の圧力の差は 1/1000 以下です。 またエアツールで使用される程度の圧縮空気では、 せいぜい 10 気圧くらいですから 1/100 以下で、非理想性の影響はあまり問題になりません。 一方、プロパンのように第 2 ビリアル係数が -400 cm3 mol-1 ぐらいにもなると、 1 気圧でも理想気体との差が 1 %ぐらいあり、その差は密度の増加とともに急速に拡大します (先にも触れましたが 8 気圧ぐらいかけると液化します)。
ビリアル状態方程式は、低密度の挙動を調べるには良いのですが、 密度が少し高くなると、どんどん高次の項を継ぎ足していく必要があります。 窒素の場合でいうと、常温で 20 気圧ぐらいまでなら第 2 ビリアル係数までの式で十分ですが、 それを超えるともっと高次の項が必要になっていきます。 そこで実在気体の状態方程式として、 液化したりする挙動も表現できるようなものが、さまざまに提案されてきました
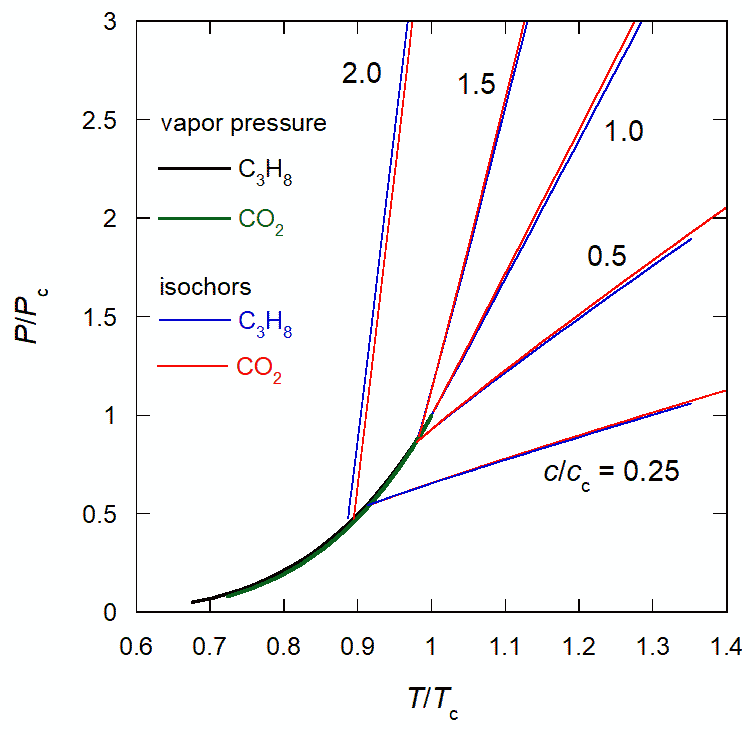
図 4. 臨界温度・圧力でスケールした、 プロパンと二酸化炭素の蒸気圧曲線と等密度線の挙動。 プロパン(黒)と二酸化炭素(緑)の蒸気圧曲線は、ほとんど重なっています。 プロパン(青)と二酸化炭素(赤)の等温線も、かなり重なります。
既知の物質の圧力・温度・密度の関係を精密に表現する、 多数のパラメーターを含む複雑なものもありますが、 図 1 や 2c の蒸気圧曲線の形状が、よく似かよっていることに注意すると、 またちがう描像も見えてきます。 図 4 には、臨界温度 Tc・圧力 Pc でスケールしたプロパンと二酸化炭素の蒸気圧曲線と、 密度一定での温度・圧力の曲線です。 密度も臨界密度 cc でスケールしてあります。 表 3 を見ると、二酸化炭素はプロパンより臨界温度は低いですが、臨界圧力は高くなっています。 それが臨界定数を単位にして記述すると、 ほとんど同じ関数形になっているのは、 ある一般的な関数で、さまざまな物質の状態方程式を記述できることを示唆します (対応状態原理 principle of corresponding state と呼ばれます)。 また等密度線がほとんど直線的なのも特徴的です(圧力係数があまり温度に依存しない)。
次のファンデルワールス van der Waals 状態方程式(1873 年)は、 分子論的な考察に基づいて、 定性的に気液の相分離や臨界現象を再現できるものとして、 気体・液体の物理化学的な研究の最初期に提案されたものです。
\begin{equation} P = \frac{cRT}{1 - bc} - a c^2 \label{eq:vdWeq} \end{equation}
ここで \(a, b\) は物質による正の定数です。 この方程式は圧力、温度、密度をスケールすることで、 物質によらない次のような関係式にまとめることができます。
\begin{equation} P^{*} = \frac{c^{*} T^{*}}{1 - c^{*}} - c^{*2} \label{eq:vdWeq2} \end{equation}
ここで \(P^{*}, T^{*}, c^{*}\) は、それぞれ \(a, b, R\) を用いて次のようにスケールした圧力、温度、密度です。
\[ P^{*} = P/(a b^{-2}),~ T^{*} = T/(R^{-1} a b^{-1}), ~ c^{*} = c/b^{-1} \]
式 \eqref{eq:vdWeq2} を見ると、 温度、圧力、密度を適宜スケールすると、物質によらず同じ関係が成り立つという、 対応状態の原理が満たされていることがわかります。
ファンデルワールス状態方程式は、 すでに図 2b のプロパンの挙動で見たように、 気体を圧縮して液体領域に入ると圧力が急増することを表現する第 1 項と(斥力項と呼ばれます)、 第 2 ビリアル係数の挙動で見たように、密度が低い領域では分子間の引力が働くという第 2 項(引力項と呼ばれます)からなっています。 そしてポイントになるのは、第 1 項が温度に比例する一方、第 2 項が温度依存性を持たないことです。 このことは、図 4 の等密度線が、ほとんど直線になっている(\(P = f(c) T + g(c)\) の形で近似できる) ことと符合します。 ファンデルワールス状態方程式にならう形で、今日に至るまで、多くの状態方程式が提案されていますが、 次のレドリッヒ-クォン Redlich-Kwon の状態方程式(1949)は、 比較的簡単で精度がよく、未知物質の状態方程式の推算などに、今も実用的に用いられています。
\begin{equation} P = \frac{cRT}{1 - bc} - \frac{a c^2}{(1 + bc)\sqrt{T}} \label{eq:RKeq} \end{equation}
ファンデルワールス状態方程式やレドリッヒ-クォンの状態方程式から、 実際に種々の物質の温度や圧力の値を推算するには、 定数 \(a, b\) を定める必要があるわけですが、 それには物質の臨界定数を用いることができます。 図 2b に見るように、臨界点は極値で変曲点にもなっており、次の条件が成り立ちます。
\begin{eqnarray} \pdifA{P}{c}{T} &=& 0; \\ \pdifA{^{2} P}{c^2}{T} &=& 0; \label{eq:CPcond} \end{eqnarray}
この関係式を解くことで、ファンデルワールス(vdW)状態方程式であれば
\begin{eqnarray} T_\mrm{c}(\mrm{vdW}) &=& \frac{8}{27} \frac{a}{Rb} \\ P_\mrm{c}(\mrm{vdW}) &=& \frac{1}{27} \frac{a}{b^2} \\ c_\mrm{c}(\mrm{vdW}) &=& \frac{1}{3} \frac{1}{b} \\ Z_\mrm{c}(\mrm{vdW}) &=& \frac{P_\mrm{c}(\mrm{vdW})}{c_\mrm{c}(\mrm{vdW}) R T_\mrm{c}(\mrm{vdW})} = \frac{3}{8} \label{eq:CPvdW} \end{eqnarray}
レドリッヒ-クォン(RK)状態方程式であれば
\begin{eqnarray} T_\mrm{c}(\mrm{RK}) &=& (2^{2/3} - 1)^2 \frac{a^{2/3}}{R^{2/3}b^{2/3}} = 0.3450 \ldots \x \frac{a^{2/3}}{R^{2/3}b^{2/3}} \\ P_\mrm{c}(\mrm{RK}) &=& \frac{(2^{1/3} - 1)^2}{2^{1/3} + 1} \frac{a^{2/3}}{R^{1/3}b^{5/3}} = 0.02989 \ldots \x \frac{a^{2/3}}{R^{1/3}b^{5/3}} \\ c_\mrm{c}(\mrm{RK}) &=& (2^{1/3} - 1) \frac{1}{b} = 0.2599 \ldots \x \frac{1}{b} \\ Z_\mrm{c}(\mrm{RK}) &=& \frac{P_\mrm{c}(\mrm{RK})}{c_\mrm{c}(\mrm{RK}) R T_\mrm{c}(\mrm{RK})} = \frac{1}{3} \label{eq:CPRK} \end{eqnarray}
という関係をえることができます。 臨界点での圧縮率係数 \(Z_\mrm{c} = P_\mrm{c}/c_\mrm{c} R T_\mrm{c}\) は、 対応状態原理が厳密に成り立っておれば、物質によらず一定になるはずですが、 実際には物質によって少し変動し、0.25 ~ 0.30 程度の値を取ります。 表 3 にも示した多種多様な物質の臨界点での圧縮率係数が、 この程度の範囲に収まることは対応状態原理の成功とも言えますし、 また不十分さとも言えるでしょう。 またそれは、ファンデルワールス状態式やレドリッヒ-クォン状態方程式の限界を教えてくれているともいえるでしょう。
臨界点での圧縮率係数 Zc = Pc/ccRTc でみた限界も踏まえ、 実際にファンデルワールス状態式などの定数 \(a, b\) を推定する際には、 通常、臨界温度 Tc と臨界圧力 Pc が使用されます。 これには図 2b にも見るように、 温度・圧力を設定した時、臨界点付近で密度が非常に大きく揺らぎ、実験的に臨界密度の精確な決定が困難であることもあずかっています。
さて圧力の温度・密度依存性だけであれば、式 \eqref{eq:vdWeq} や式 \eqref{eq:RKeq} のような形でよいのですが、 化学熱力学的には、混合物・溶液の扱いが気になるところです。 簡単のため 2 成分(1 と 2 とします)について見ると、ファンデルワールス状態方程式や レドリッヒ-クォン状態方程式では、次のような取り扱いが普通です。
\begin{eqnarray} c &=& c_{1} + c_{2} \label{eq:1fluid} \\ a c^2 &=& a_{11} c_1^2 + 2a_{12} c_1 c_2 + a_{22} c_2^2 = (a_{11} x_1^2 + 2a_{12} x_1 x_2 + a_{22} x_2^2) c^2 \label{eq:mixrule1} \\ b c &=& b_{11} c_1 + b_{22} c_2= (b_{11} x_1 + b_{22} x_2) c \label{eq:mixrule2} \end{eqnarray}
ここで \(x_1, x_2\) はモル分率 \(x_1 = n_1/(n_1 + n_2) = c_1/(c_1 + c_2) = 1 - x_2\) です。 パラメータの添え字 11, 22 は、それぞれ純粋な 1、2 についてのパラメータを意味します。 式 \eqref{eq:mixrule1} は、そこに相互作用の効果を評価するパラメータ \(a_{12}\) の項が加わった形です。 \(b\) についての式 \eqref{eq:mixrule2} に \(b_{12}\) の項がないのは、 \(a\) についての式 \eqref{eq:mixrule1} 同様の \(x_1, x_2\) の 2 次式で、 \(b_{12} = (b_{11} + b_{22})/2\) としたことに相当します。
式 \eqref{eq:1fluid} - \eqref{eq:mixrule2} のアイデアは古く 19 世紀のファンデルワールスにもさかのぼるもので、 成分が増えても、密度だけ取り出せばあたかも 1 成分の流体のようにふるまうと考え、 パラメータにそれぞれの成分の寄与を簡単な 2 次形式の形で取り入れたものです。 しかしこれでも実際の混合物の挙動の推算等には十分複雑で、 今もさまざまな試みが続いています。
なお蒸発・凝縮がどの状態で起きるのかといった問題については、ここで扱った温度・圧力からさらに進んで、 化学ポテンシャルを考える必要があります。 この問題にはまた後ほど触れます。
ただし古くからの基準の切り替えには慎重な向きも多く、 今も都市ガスや排ガスなどの容量の算定には、0 °C、1 atm での体積が使用されています (Nm3 あるいは m3N と表記されます (業界ではノルマルリューベ(ノルマル立米。平米同様、日本語です)などと読みます))。