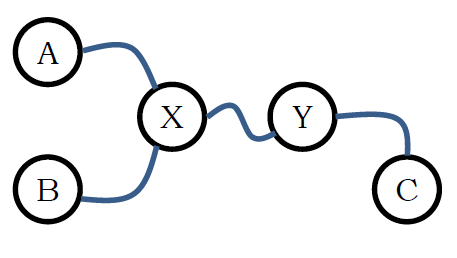

1.【2018試験問題】 水準測量では、標高の知れた地点(水準点)から、見通しのきく適当な経路に沿って100 m程度の間隔で測量を何度も繰り返し、 未知の地点の標高を決定する。 図のような経路に沿って、3つの水準点A、B、Cから水準測量を行った場合を考える。 この時、最小2乗法によって X と Y の標高 x、y を定めるのに、 次のSが最小になるようにすればよいという。
\[ S = \frac{(a + h_{\rm{AX}} - x)^2}{L_{\rm{AX}}} + \frac{(b + h_{\rm{BX}} - x)^2}{L_{\rm{BX}}} + \frac{(c + h_{\rm{CY}} - y)^2}{L_{\rm{CY}}} + \frac{(x + h_{\rm{XY}} - y)^2}{L_{\rm{XY}}} ~~~ \rm{(X)} \]
ここで a、b、c はそれぞれ水準点 A、B、C の標高であり、 hPQ は測量で得られた P から見た Q の標高差、LPQ は P から Q までの経路の長さである。
1-1.測量で得られる標高差の値の分散がおよそ経路の長さに比例すると考えて、 式(X)が導かれているという(“コンパス・ルール”)。 測量値の分散が経路の長さに比例すると考えてよいのはなぜか、教員(Yの方)にも分かるように説明せよ。
| P | Q | LPQ / km | hPQ / m |
| A | X | 2.0 | -11.654 |
| B | X | 4.0 | -3.152 |
| C | Y | 3.0 | -9.881 |
| X | Y | 1.0 | 8.875 |
1-2.a = 18.225 m、b = 9.673 m、c = 25.358 mで、各経路の測量値は右表のとおりであったとする。 最小2乗法に基づいてXとYの標高を定めよ。
一回ごとの水準測量はそれぞれ独立に行われ、測量値の分散が同じと見なせるだろう。 したがってその総和の分散は測定回数に比例する。 測定回数はおよそ経路の長さに比例すると考えられるので、得られる標高差の分散は経路の長さに比例すると考えてよい。
ax = a + hAX = 6.571 m
bx = b + hBX = 6.521 m
cy = c + hCY = 15.477 m
とする。
式 (X) から、正規方程式は次のように書ける:
\[ -\frac{1}{2} \frac{\partial S}{\partial x} = \frac{a_x - x}{L_{AX}} + \frac{b_x - x}{L_{BX}} - \frac{x +h_{xy} - y}{L_{XY}} = 0\\ -\frac{1}{2} \frac{\partial S}{\partial y} = \frac{c_y - y}{L_{CY}} + \frac{x +h_{xy} - y}{L_{XY}} = 0\\ \]
ここから \(y\) については
\[ \left( \frac{1}{L_{CY}} + \frac{1}{L_{XY}} \right) y = \frac{c_y}{L_{CY}} + \frac{x + h_{xy}}{L_{XY}}\\ y = \frac{L_{XY}}{L_{CY} + L_{XY}} c_y + \frac{L_{CY}}{L_{CY} + L_{XY}} (x + h_{xy}) \]
\(x\) は
\[ \left(\frac{1}{L_{AX}} + \frac{1}{L_{BX}} +\frac{1}{L_{XY}} \right) x = \frac{a_x}{L_{AX}} + \frac{b_x}{L_{BX}} + \frac{y - h_{xy}}{L_{XY}} \]
ここに \(y\) の式を代入すると
\[ \left(\frac{1}{L_{AX}} + \frac{1}{L_{BX}} +\frac{1}{L_{XY}} \right) x = \frac{a_x}{L_{AX}} + \frac{b_x}{L_{BX}} + \frac{c_y - h_{xy}}{L_{CY} + L_{XY}} + \frac{1}{L_{XY}} \frac{L_{CY}}{L_{CY} + L_{XY}} x \]
したがって \(x\) は
\[ \left(\frac{1}{L_{AX}} + \frac{1}{L_{BX}} +\frac{1}{L_{CY} + L_{XY}} \right) x = \frac{a_x}{L_{AX}} + \frac{b_x}{L_{BX}} + \frac{c_y - h_{xy}}{L_{CY} + L_{XY}} \]
与えられた数値を代入すると
\[ \left(\frac{1}{2} + \frac{1}{4} +\frac{1}{4} \right) x = \frac{6.571}{2} + \frac{6.521}{4} + \frac{15.477 ~ - ~8.875}{4} \]
より、x = 6.566。 y は 15.450。
X: 6.566 m、Y: 15.450 m