昔、PC の使用が一般的でなかった時代、 実験データに最小2乗法を適用するのは面倒な仕事でした。 ぼくの学生時代はもう関数電卓が使える時代でしたから、まだ楽でしたが、 それでも最小2乗法の計算では、いわゆるケタ落ちが起きやすく、中間の計算結果を何ケタとるかなど、 かなり気を遣う作業です。 その昔はもっと大変で、ぼくは最小2乗法を使わずにもっともらしい直線を引く「裏技」的なやり方を聞いた記憶があります (データを前半後半に分けて、それぞれの平均点を結んでもっともらしい直線にする)。
それが昔と違って最小2乗法は excel などの一般的なソフトにも組み込まれ、 特にその背景を知らなくても使える時代になりました。 非線形の最小2乗法も、「科学技術用」を標榜するグラフ作成ソフトには標準で入っています。 今日、ふつう化学で使う最小2乗法は、小学校でも習うような、 いわば「平均」を取る操作になっていると言っていいかもしれません。
特に化学では、そもそもの直線関係(あるいは何らかの関係)が成立しているかどうかより、 そこから得られるパラメーターの方にもっぱら関心があることが多いようです (関係の成立は「見ればわかる」)。 ですから生物や経済などの分野のように、 相関の検定などにはあまり注意が払われません。 その結果、最小2乗法の手続きの詳細はしばしば「ブラックボックス」になってしまい、 思わぬ罠にはまってしまうことがあるようです。
というところで、過去の時代の空気を少し嗅いだものとして、 ここではできるだけ実際に化学実験で出会うような話題を中心に、 あまり統計の深い事情には関わらない形で、 しばしば見落とされがちな話題を中心に問題を構成しています。

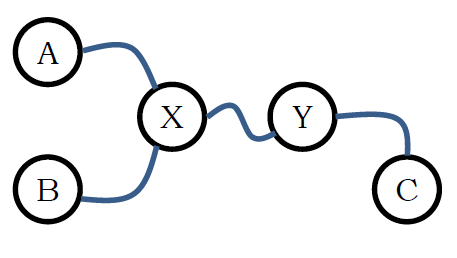
1.【2018試験問題】 水準測量では、標高の知れた地点(水準点)から、見通しのきく適当な経路に沿って100 m程度の間隔で測量を何度も繰り返し、 未知の地点の標高を決定する。 図のような経路に沿って、3つの水準点A、B、Cから水準測量を行った場合を考える。 この時、最小2乗法によって X と Y の標高 x、y を定めるのに、 次のSが最小になるようにすればよいという。
\[ S = \frac{(a + h_{\rm{AX}} - x)^2}{L_{\rm{AX}}} + \frac{(b + h_{\rm{BX}} - x)^2}{L_{\rm{BX}}} + \frac{(c + h_{\rm{CY}} - y)^2}{L_{\rm{CY}}} + \frac{(x + h_{\rm{XY}} - y)^2}{L_{\rm{XY}}} ~~~ \rm{(X)} \]
ここで a、b、c はそれぞれ水準点 A、B、C の標高であり、 hPQ は測量で得られた P から見た Q の標高差、LPQ は P から Q までの経路の長さである。
1-1.測量で得られる標高差の値の分散がおよそ経路の長さに比例すると考えて、 式(X)が導かれているという(“コンパス・ルール”)。 測量値の分散が経路の長さに比例すると考えてよいのはなぜか、教員(Yの方)にも分かるように説明せよ。
| P | Q | LPQ / km | hPQ / m |
| A | X | 2.0 | -11.654 |
| B | X | 4.0 | -3.152 |
| C | Y | 3.0 | -9.881 |
| X | Y | 1.0 | 8.875 |
1-2.a = 18.225 m、b = 9.673 m、c = 25.358 mで、各経路の測量値は右表のとおりであったとする。 最小2乗法に基づいてXとYの標高を定めよ。
2.N 個の一連のデータ (x1, y1), (x2, y2), ..., (xN, yN)を、 測定値 yi の分散が xi によらず σ2 で一定であるとして、 y = ax という関係式に最小2乗法であてはめることを考える。 Sx = Σ xi、 Sy = Σ yi、 Sxx = Σ xi2、 Sxy = Σ xiyi、 Syy = Σ yi2 を用いて推定される係数 a を表せ。 また推定される係数aの分散 ⟨⟨ a2 ⟩⟩ はどのようにあらわされるか?
3.K大学の優秀な学生たちが、温度を90 °Cに保ったホットプレートスターラーの天板上に水を入れたビーカーを乗せ、 熱電対を用いて最終到達温度を調べた。下表は、ビーカーに入れた水の体積Vと最終到達温度tの27グループ分の結果である。
| V/mL | t /°C | V/mL | t /°C | V/mL | t /°C | V/mL | t /°C | V/mL | t /°C | V/mL | t /°C |
| 40 | 79 | 80 | 79 | 50 | 83 | 50 | 76 | 80 | 75 | 50 | 77 |
| 20 | 74 | 18 | 82 | 40 | 79 | 60 | 84 | 80 | 74 | 40 | 78 |
| 75 | 77 | 40 | 77 | 50 | 80 | 50 | 80 | 50 | 77 | ||
| 60 | 80 | 47 | 80 | 40 | 82 | 50 | 75 | 65 | 76 | ||
| 40 | 76 | 60 | 77 | 50 | 79 | 50 | 80 | 65 | 75 |
3-1.最終到達温度 t とビーカーに入れた水の体積 V との間に、t = aV + b という関係が成立するものとして、 最小2乗法を用いて係数 a と b を定めよ。
3-2.最終到達温度 t の標準偏差が 2.0 °C であることが分かっているとする。 推定した係数 a と b の標準偏差を求めよ。
3-3.ビーカーに入れた水の体積と最終到達温度が無関係であるという主張は、 係数 a = 0 であるという主張と同じであると考えることができる。 この実験結果から、有意水準 5 %で、最終到達温度はビーカーに入れた水の体積と無関係に決まると言ってよいかどうか判定せよ。
4.表に示すのは某 K 大学の学生たち17グループが、1.0 mol/Lの塩酸とその10倍希釈液(0.10 mol/L)のpHの値を、pH計を用いて測定した結果である。
| group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1.0 M | 1.18 | 1.20 | 0.81 | 1.09 | 1.09 | 0.93 | 1.20 | 0.92 | 1.15 | 1.30 |
| 0.10 M | 0.01 | 0.23 | -0.15 | 0.08 | 0.05 | -0.09 | 0.09 | -0.13 | 0.25 | 0.12 |
| group | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||
| 1.0 M | 1.17 | 1.10 | 1.02 | 1.30 | 1.01 | 1.06 | 1.09 | |||
| 0.10 M | 0.17 | 0.24 | 0.05 | 0.30 | 0.04 | 0.02 | 0.22 |
4-1.横軸(x)に1.0 M の pH、縦軸(y)に 0.10 M の pH をとってプロットし、 最初2乗法を用いて y = ax + b という直線に当てはめて、係数 a、b を定めよ。 また相関係数はいくらになるか。 横軸(x)に0.1 M の pH、縦軸(y)に 1.0 M の pH をとってプロットしたらどうなるか?
4-2.縦軸と横軸を入れ替えた時に得られる直線の勾配が、 逆数の関係にならないのはなぜだろうか?
| T / K | 1000 k / s-1 |
| 300.0 | 2.19 |
| 310.0 | 4.33 |
| 320.0 | 8.83 |
| 330.0 | 17.1 |
5.【15年度試験問題から】ある1次反応について温度Tを変えて反応速度定数kを測定し表のような結果を得た。 速度定数の相対誤差は、標準偏差にして3.0 %で一定であるという。 速度定数 k の温度依存性が、アレニウスの式
k = A exp(-Ea/RT)
で精度よく表現できる(Aは前指数因子、Eaは活性化エネルギー、 Rは気体定数8.31 J K-1 mol-1)ものとしてこのデータを解析した以下の文章を読み、 問いに答えよ。
アレニウスの式から、x = 1000/(T/K)、y = ln(1000 k / s-1)とすると
y = a x + b
という直線関係が成立する。 (1) 速度定数の相対誤差が同じだから、y の誤差(標準偏差)は x によらず一定と見なせ、 係数 a と b はよく使われる最小2乗法の公式
\[ a = \frac{N S_{xy} - S_x S_y}{N S_{xx} - S_x^2}, ~~ b = \frac{S_y - a S_x}{N} \]
を用いてa = イ 、b = ロ と評価できる。 またyの分散を σ2とすると、a、bの分散 σa2、 σb2 はそれぞれ次式
\[ \sigma_a^2 = \frac{N}{N S_{xx} - S_x^2} \sigma^2, ~~ \sigma_b^2 = \frac{S_{xx}}{N S_{xx} - S_x^2} \sigma^2 \]
で評価できるので、a 、bの標準偏差はそれぞれ ハ 、 ニ になる。 もとのアレニウスの式に立ち返ると、 前指数因子A、活性化エネルギーはそれぞれ
ln A/s-1 = ホ ± ヘ
Ea / kJ mol-1 = ト ± チ
ということになる(± 以下は標準偏差)。
さて得られたアレニウスの式を用いて、T = 315 Kの場合について速度定数を推定した時の誤差を考えよう。 これは x’ = (1/(T/K) - 1/315)として、データを y = px’ + q という式に当てはめた時の q の誤差に相当し、 315 Kでの相対誤差は標準偏差にして リ %になる。 この時の p、q の分散の値 σp2、σq2を用い、 (2) 350 Kにおける速度定数の推定値の分散は σp2 (1/350 - 1/315)2 + σq2 でおよそ評価でき、 350 Kでの相対誤差は標準偏差にして ヌ %になる。
5-1.文中の イ~ヌ に当てはまる適切な数値を記せ。
5-2.下線部 (1) が成立する根拠を教員(Yの方)にもわかるように説明せよ。
5-3.下線部 (2) のように言える根拠を教員(Yの方)にもわかるように説明せよ。
| λ / nm | A | B | Y |
| 430 | 0.780 | 0.194 | 0.227 |
| 455 | 0.059 | 0.358 | 0.061 |
| 615 | 0.116 | 0.027 | 0.040 |
| 644 | 0.108 | 0.096 | 0.040 |
| 662 | 0.603 | 0.018 | 0.152 |
6.【16年度試験問題から】ホウレン草からクロロフィルを抽出し、 カラムクロマトグラフィーでクロロフィルa(Chl a)とクロロフィルb(Chl b)が溶離してくる分画ごとの吸収スペクトルをとった。 表にまとめたのは、ほぼ純粋なChl aを含む分画Aとほぼ純粋なChl bを含む分画B、 そしてそのその中間の分画Yのいくつかの波長 λ における吸光度の値である。 Yの波長 λ における吸光度 Y(λ) が、Aの吸光度 A(λ) とBの吸光度 B(λ) を用いて
Y(λ) = a A(λ) + b B(λ)
と表され、各波長における吸光度の標準偏差はほぼ一定であるとし、最小2乗法の取り扱いにならって、残差2乗和
S = Σ [Y(λ) - a A(λ) - b B(λ)]2
が最も小さくなるように係数a、bを定めることを考える。ここで Σ はすべての波長データについての和を取るものとする。
6-1.Spq = Σ p(λ) q(λ) として、 a と b を SAA、SAB、SBB、SAY、SBYを用いて表せ。
6-2.表のデータを用いてaとbを求めよ。
7.【2011試験問題】以下の文章を読み、問に答えよ。
25 °C で濃度を変化させて、水相とベンゼン相に分配される塩化水銀(II)の平衡濃度 cW、cB を測定して次の結果を得た(1 mM = 0.001 mol/L):
| cW/mM | 233 | 158 | 111.2 | 64.8 | 7.38 | 1.84 |
| cB/mM | 17.3 | 12.22 | 8.86 | 5.24 | 0.618 | 0.155 |
水中で塩化水銀はほとんど解離せず HgCl2 として溶存し、 一部会合してHg2Cl4となっており、 ベンゼン中では HgCl2 として溶けていると考えよう。 すると水中の塩化水銀濃度 cW は単量体濃度 cW(M) と二量体濃度 cW(D) の和 cW(M) + 2cW(D) で表され、 ベンゼン中濃度 cB は単量体濃度 cB(M)に等しい。 ここで(1)水とベンゼンの間の単量体の分配定数 Kp、 (2) 水中の 2HgCl2 ⇔ Hg2Cl4の平衡定数 Kd を考えると、 それぞれ次の関係が成り立つ:
Kp = cW(M) / cB、Kd = cW(D) / cW(M)2
したがって次式が成り立つ:
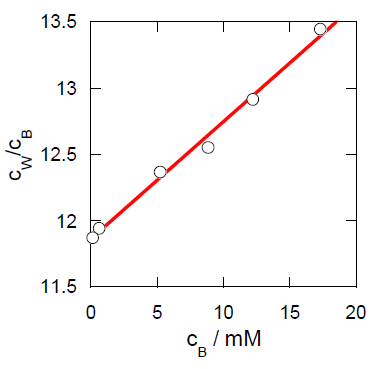
cW/cB = イ + ロ cB
つまりcW/cB を cB に対してプロットすれば直線関係が得られ、 切片と勾配からKp、Kdが定まる。 実際にプロットすると図のような直線関係が得られた。
7-1.文中 イ、 ロ にあてはまる係数を Kp、Kd を用いて表わせ。
7-2.図のプロットに対し最小2乗法を用いて イ、ロ を求めたところ、イ =11.86、ロ = 0.089 / mM であった。 2量化平衡定数 Kd を求めよ。
7-3.最小2乗法で推定された イ、ロ の標準偏差は イ が0.04、ロ は 0.004 /mMであった。 上で得られた2量化平衡定数 Kd の標準偏差を評価せよ。(イ と ロ が統計的に独立でないことに注意)
8.表に示すのは 某K 大学の学生の A、B、2グループが、 0.20 mol/L の塩酸と0.10 mol/L の酢酸を、イオン交換水で2倍に希釈するごとにpHの値を測定した結果である。 1回希釈するごとに濃度が半分になるので、希釈のたびごとにpHは強酸であれば0.30、弱酸であれば0.15大きくなることが期待される。
| 希釈回数 | 0 | 1 | 2 | 3 | 4 | 5 |
| A | 0.76 | 1.02 | 1.3 | 1.58 | 1.9 | 2.2 |
| B | 0.97 | 1.28 | 1.56 | 1.86 | 2.14 | 2.45 |
| 希釈回数 | 0 | 1 | 2 | 3 | 4 | 5 |
| A | 2.81 | 2.94 | 3.07 | 3.27 | 3.44 | 3.62 |
| B | 2.98 | 3.13 | 3.26 | 3.46 | 3.6 | 3.72 |
8-1.なぜ希釈のたびごとに強酸の pH が 0.30、弱酸の pH は 0.15 大きくなることが期待されるかを簡潔に述べよ。
8-2.塩酸、酢酸それぞれについて、希釈回数 n に対しA、B 両グループの測定したpHの値をプロットせよ。
8-3.pH が n に対し pH = an + b という関係を満たすものとして、 最小2乗法を用い、A、B 両グループそれぞれについて、 塩酸、酢酸の場合のパラメーターa、bとその標準偏差を定めよ。 pH 測定の標準偏差を0.02 とする。
8-4. 最小2乗法で得た残差2乗和の期待値が分散の N - 2 倍になることから、これで測定値の分散を評価することができる。 こうして評価したpH測定の標準偏差を、それぞれの場合について求めて比較して見よ。
8-5.A、B両グループの測定結果の差異が、pH計の較正ミスによるもので、 測定値からある一定の値を差し引けばなくなるものとしよう。 この場合、A、B両グループについて、pH = an + bという関係式において a は共通で b が異なる取り扱いをして最小2乗法を適用すればよいと考えられる。 どのような取り扱いをすればよいか考察せよ。
9.【直交多項式】 次のような k 次の多項式 Qk(x)を考える(N は自然数):
Q0(x) = 1,
Q1(x) = 1 - 2 (x/N),
Q2(x) = 1 - 6 (x/N) + 6 (x[2]/N[2]),
Q3(x) = 1 - 12 (x/N) + 30 (x[2]/N[2]) - 20 (x[3]/N[3]),
Q4(x) = 1 - 20 (x/N) + 90 (x[2]/N[2]) - 140 (x[3]/N[3]) + 70 (x[4]/N[4]) ,
....
ここで p[n]は階乗関数で p(p - 1)(p - 2) … (p - n + 1) を表す。
9-1.N = 5 の場合について Q0(x)、Q1(x)、Q2(x)、Q3(x) のグラフを書け(0 ≤ x ≤ N)。
9-2.N = 5 の場合について、m ≠ n ならば Σ [Qm(i) Qn(i)] = 0となることを確認せよ。 ここでは Σ i = 0から N までの総和を取る。
9-3.等しい間隔 h で取られた N + 1 個のデータ(i h, yi)(i = 0, 1, …, N)に対し、 m 次の多項式 y(t) = a0 Q0(t/h) + a1 Q1(t/h) + … + am Qm(t/h) を最小2乗法を用いてあてはめる。 この時、係数ajが Σ [Qj(i)yj]/ Σ [(Qj(i))2]で与えられることを示せ。
ここで扱う Qk(x) は、チェビシェフの多項式と呼ばれる。 ただし cos(k cos-1 x) で与えられる有名なものとは異なるので注意。