4.表に示すのは某 K 大学の学生たち17グループが、1.0 mol/Lの塩酸とその10倍希釈液(0.10 mol/L)のpHの値を、pH計を用いて測定した結果である。
| group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1.0 M | 1.18 | 1.20 | 0.81 | 1.09 | 1.09 | 0.93 | 1.20 | 0.92 | 1.15 | 1.30 |
| 0.10 M | 0.01 | 0.23 | -0.15 | 0.08 | 0.05 | -0.09 | 0.09 | -0.13 | 0.25 | 0.12 |
| group | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||
| 1.0 M | 1.17 | 1.10 | 1.02 | 1.30 | 1.01 | 1.06 | 1.09 | |||
| 0.10 M | 0.17 | 0.24 | 0.05 | 0.30 | 0.04 | 0.02 | 0.22 |
4-1.横軸(x)に1.0 M の pH、縦軸(y)に 0.10 M の pH をとってプロットし、 最初2乗法を用いて y = ax + b という直線に当てはめて、係数 a、b を定めよ。 また相関係数はいくらになるか。 横軸(x)に0.1 M の pH、縦軸(y)に 1.0 M の pH をとってプロットしたらどうなるか?
4-2.縦軸と横軸を入れ替えた時に得られる直線の勾配が、 逆数の関係にならないのはなぜだろうか?

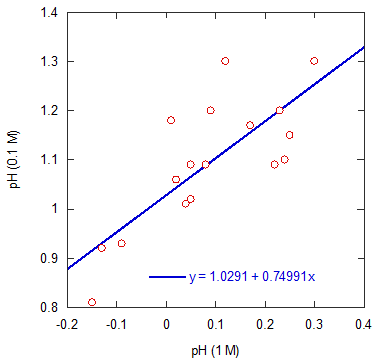
横軸(x)に1.0 M の pH、縦軸(y)に 0.10 M の pH をとってプロットした結果は、 右図のようになる。 最小2乗法で y = ax + b という直線に当てはめた結果は、
a = 0.750
b = 1.029
相関係数 ρ は 0.772 となる。 縦軸、横軸を逆にして、横軸(x)に0.1 M の pHをとり、 最小2乗法で y = ax + b に当てはめた結果は、
a = 0.794
b = -0.782
となる。 相関係数は上と同じく 0.772 である。
最小2乗法で y = ax + b に当てはめて求められる勾配 a は
\[ a = \frac{N S_{xy} - S_x S_y}{N S_{xx} - S_x^2} \]
で与えられる。 一方、x, y を逆にして x = cy + d から最小2乗法で求められる勾配 c は
\[ c = \frac{N S_{xy} - S_x S_y}{N S_{yy} - S_y^2} \]
したがって a と c は
\[ a c = \frac{(N S_{xy} - S_x S_y)^2}{(N S_{xx} - S_x^2)(N S_{yy} - S_y^2)} = \rho^2 \le 1 \]
より、逆数の関係になく、両者の積は相関係数の2乗(決定係数)に等しく、一般に 1 より小さい。