問 7

７．【2011試験問題】以下の文章を読み、問に答えよ。

25 °C で濃度を変化させて、水相とベンゼン相に分配される塩化水銀(II)の平衡濃度 c_W、c_B を測定して次の結果を得た（1 mM = 0.001 mol/L）：

cW/mM	233	158	111.2	64.8	7.38	1.84
cB/mM	17.3	12.22	8.86	5.24	0.618	0.155

水中で塩化水銀はほとんど解離せず HgCl₂ として溶存し、 一部会合してHg₂Cl₄となっており、 ベンゼン中では HgCl₂ として溶けていると考えよう。 すると水中の塩化水銀濃度 c_W は単量体濃度 c_W(M) と二量体濃度 c_W(D) の和 c_W(M) + 2c_W(D) で表され、 ベンゼン中濃度 c_B は単量体濃度 c_B(M)に等しい。 ここで(1)水とベンゼンの間の単量体の分配定数 K_p、 (2) 水中の 2HgCl₂ ⇔ Hg₂Cl₄の平衡定数 K_d を考えると、 それぞれ次の関係が成り立つ：

K_p = c_W(M) / c_B、K_d = c_W(D) / c_W(M)²

したがって次式が成り立つ：

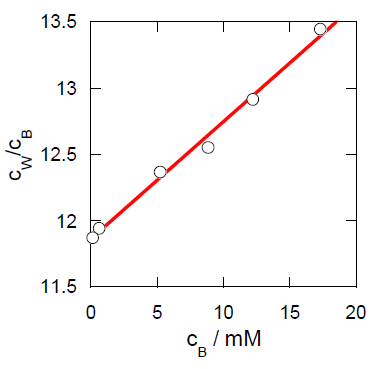
　c_W/c_B = 　イ　 + 　ロ　 c_B

つまりc_W/c_B を c_B に対してプロットすれば直線関係が得られ、 切片と勾配からK_p、K_dが定まる。 実際にプロットすると図のような直線関係が得られた。

７-１．文中 イ、 ロ にあてはまる係数を K_p、K_d を用いて表わせ。

７-２．図のプロットに対し最小２乗法を用いて イ、ロ を求めたところ、イ =11.86、ロ = 0.089 / mM であった。 ２量化平衡定数 K_d を求めよ。

７-３．最小２乗法で推定された イ、ロ の標準偏差は イ が0.04、ロ は 0.004 /mMであった。 上で得られた２量化平衡定数 K_d の標準偏差を評価せよ。（イ と ロ が統計的に独立でないことに注意）

解答例

7-1

水層中の塩化水銀の全濃度 c_W の式について、与えられた平衡関係を整理すると

c_W = c_W(M) + 2c_W(D)
= c_W(M) + 2 K_d c_W(M)²
= K_p c_B + 2K_d [K_p c_B]²

より　　【イ】【ロ】

c_W/c_B = K_p + 2K_d K_p² c_B

7-2

先に得た関係式から、値を代入すれば

Kd = ロ/2 K_p² =ロ/ 2イ²
= 3.16 × 10^-4 mM^-1

7-3

y = ax + b という式に最小２乗法で当てはめて推定されるパラメータ a、b について、 a の分散 ⟨⟨ a² ⟩⟩ と共分散 ⟨⟨ ab ⟩⟩ の間には、 次の関係が成立する（ \(\bar{x}\) はxの標本平均）。

\[ \langle \langle ab \rangle \rangle = -\bar{x} \langle \langle a^2 \rangle \rangle \]

表の c_Bの平均は 7.4 mM なので、

⟨⟨ ab ⟩⟩ = -7.4 mM × (0.004 mM^-1)² = -1.2 × 10^-4 mM^-1

２量化平衡定数は a/2b² で評価されている。 a° + δa、a° + δa という不確かさを含む量として a/2b² を書くと

K_d = a/2b² ≈ (a°/2b°²)(1 + (δa/a°) - 2(δb/b°))

したがって得られる二量化の平衡定数の分散 ⟨⟨ K_d² ⟩⟩ は

⟨⟨ K_d² ⟩⟩/K°_d²
= ⟨⟨ a² ⟩⟩/a°² - 4 ⟨⟨ ab ⟩⟩/(a° b°) + 4⟨⟨ b² ⟩⟩/b°²
= (0.004/0.089)² + 4 × 1.2 × 10^-4/(0.089 × 11.86) + 4 × (0.04/11.86)²
= 2.0 × 10^-3 + 4.5 × 10^-4 + 4.5 × 10^-5 = 2.5 × 10^-3

K_d の標準偏差はその 5 %、1.6 × 10^-5 mM^-1 ということになる。