 |
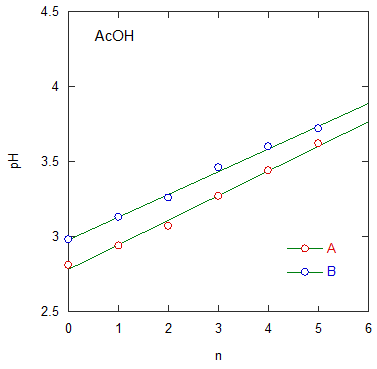 |
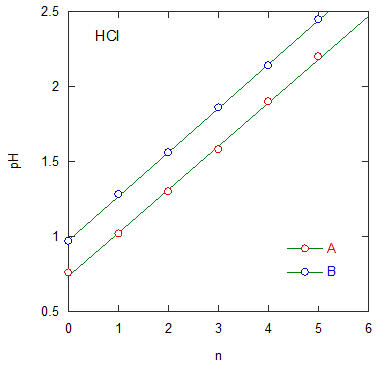
| 0.2 M 塩酸の順次2倍希釈にともなうpH 変化 | 0.1 M 酢酸の順次2倍希釈にともなうpH 変化 |
8.表に示すのは 某K 大学の学生の A、B、2グループが、 0.20 mol/L の塩酸と0.10 mol/L の酢酸を、イオン交換水で2倍に希釈するごとにpHの値を測定した結果である。 1回希釈するごとに濃度が半分になるので、希釈のたびごとにpHは強酸であれば0.30、弱酸であれば0.15大きくなることが期待される。
| 希釈回数 | 0 | 1 | 2 | 3 | 4 | 5 |
| A | 0.76 | 1.02 | 1.3 | 1.58 | 1.9 | 2.2 |
| B | 0.97 | 1.28 | 1.56 | 1.86 | 2.14 | 2.45 |
| 希釈回数 | 0 | 1 | 2 | 3 | 4 | 5 |
| A | 2.81 | 2.94 | 3.07 | 3.27 | 3.44 | 3.62 |
| B | 2.98 | 3.13 | 3.26 | 3.46 | 3.6 | 3.72 |
8-1.なぜ希釈のたびごとに強酸の pH が 0.30、弱酸の pH は 0.15 大きくなることが期待されるかを簡潔に述べよ。
8-2.塩酸、酢酸それぞれについて、希釈回数 n に対しA、B 両グループの測定したpHの値をプロットせよ。
8-3.pH が n に対し pH = an + b という関係を満たすものとして、 最小2乗法を用い、A、B 両グループそれぞれについて、 塩酸、酢酸の場合のパラメーターa、bとその標準偏差を定めよ。 pH 測定の標準偏差を0.02 とする。
8-4. 最小2乗法で得た残差2乗和の期待値が分散の N - 2 倍になることから、これで測定値の分散を評価することができる。 こうして評価したpH測定の標準偏差を、それぞれの場合について求めて比較して見よ。
8-5.A、B両グループの測定結果の差異が、pH計の較正ミスによるもので、 測定値からある一定の値を差し引けばなくなるものとしよう。 この場合、A、B両グループについて、pH = an + bという関係式において a は共通で b が異なる取り扱いをして最小2乗法を適用すればよいと考えられる。 どのような取り扱いをすればよいか考察せよ。
強酸では完全解離が実現する結果(HA → H+ + A-)、 水の自己プロトリシスに由来する水素イオン濃度(pH 7)より、酸濃度 c(= [HA] + [A-])が十分高ければ pH は - log c/M にほぼ等しい(M = mol/L)。 したがって2倍に希釈した場合、pH は log 2 ≅ 0.30 大きくなる。 弱酸では、酸解離平衡 HA ↔ H+ + A- の解離定数 Ka に比べて酸濃度 c が大きければ、 (そして水の自己プロトリシスに由来する水素イオン濃度より、酸解離で生成する共役塩基濃度 [A-] が十分高ければ)
Ka [HA] ≈ Ka c = [H+][A-] ≈ [H+]2
の関係が成立し、pH については整理すると次式になる。
2 pH = pKa - log c
したがって2倍に希釈した場合、pH は (1/2) log 2 ≅ 0.15 大きくなる。
与えられたA、B 両グループのデータをプロットすると次のようになる。
 |
 |
| 0.2 M 塩酸の順次2倍希釈にともなうpH 変化 | 0.1 M 酢酸の順次2倍希釈にともなうpH 変化 |
与えられたデータを、それぞれ最小2乗法で直線に当てはめて、勾配 a と切片 b を求め、 それぞれのパラメータの標準偏差を、pH データの標準偏差を 0.02 として評価すると、次表のようになる(± 以下は標準偏差)。
| HCl | a | b |
|---|---|---|
| A | 0.289 ± 0.005 | 0.737 ± 0.014 |
| B | 0.294 ± 0.005 | 0.976 ± 0.014 |
| AcOH | a | b |
|---|---|---|
| A | 0.164 ± 0.005 | 2.781 ± 0.014 |
| B | 0.152 ± 0.005 | 2.979 ± 0.014 |
なおパラメーターの標準偏差は、使用したデータの希釈回数と、想定した pH データの標準偏差で決まるので、 今回の場合、塩酸と酢酸、グループ A と B で、勾配 a と切片 b の標準偏差は同じものになる。
残差2乗和の最小値 Smin は Syy - [a Sxy + b Sy] で与えられる。 ここから pH の標本分散を Smin/ (N - 2) で評価して得た、 pH の標本標準偏差 σ(eval) を次の表に示す。
| 塩酸 | 酢酸 | |
|---|---|---|
| A | 0.021 | 0.026 |
| B | 0.009 | 0.021 |
問題で与えられた標準偏差 0.02 と一致していると見なせる。
y = an + bという関係式を、2つのデータセット A、B に当てはめるとき、a が共通で b が異なるということは、 残差2乗和を、パラメータ a, bA, bB を用いて次の形で書き、 (a, bA, bB) についてその極値を求めるという問題だと考えられる。
\[ S = \sum_{\rm{A}} [y_i - (a x_i + b_{\rm{A}})]^2 + \sum_{\rm{B}} [y_i - (a x_i + b_{\rm{B}})]^2 \]
ここから得られる正規方程式は、次のように書ける。
\[ -\frac{1}{2} \frac{\partial S}{\partial a} = -\sum_{\rm{A}, \rm{B}} x_i y_i + a \sum_{\rm{A}, \rm{B}} x_i^2 + b_{\rm{A}} \sum_{\rm{A}} x_i + b_{\rm{B}} \sum_{\rm{B}} x_i = 0\\ -\frac{1}{2} \frac{\partial S}{\partial b_{\rm{A}}} = -\sum_{\rm{A}} y_i + a \sum_{\rm{A}} x_i + b_{\rm{A}} N_{\rm{A}} = 0\\ -\frac{1}{2} \frac{\partial S}{\partial b_{\rm{B}}} = -\sum_{\rm{B}} y_i + a \sum_{\rm{B}} x_i + b_{\rm{B}} N_{\rm{B}} = 0 \]
総和を略記して書くと、次の連立方程式の解として、パラメーター(a, bA, bB) が得られることになる。
\[ S_{xx}^{\rm{A, B}} a + S_x^{\rm{A}} b_{\rm{A}} + S_x^{\rm{B}} b_{\rm{B}} = S_{xy}^{\rm{A, B}}\\ S_{x}^{\rm{A}} a + S_x^{\rm{A}} b_{\rm{A}} = S_{y}^{\rm{A}}\\ S_{x}^{\rm{B}} a + S_x^{\rm{B}} b_{\rm{B}} = S_{y}^{\rm{B}}\\ \]