9.【直交多項式】 次のような k 次の多項式 Qk(x)を考える(N は自然数):
Q0(x) = 1,
Q1(x) = 1 - 2 (x/N),
Q2(x) = 1 - 6 (x/N) + 6 (x[2]/N[2]),
Q3(x) = 1 - 12 (x/N) + 30 (x[2]/N[2]) - 20 (x[3]/N[3]),
Q4(x) = 1 - 20 (x/N) + 90 (x[2]/N[2]) - 140 (x[3]/N[3]) + 70 (x[4]/N[4]) ,
....
ここで p[n]は階乗関数で p(p - 1)(p - 2) … (p - n + 1) を表す。
9-1.N = 5 の場合について Q0(x)、Q1(x)、Q2(x)、Q3(x) のグラフを書け(0 ≤ x ≤ N)。
9-2.N = 5 の場合について、m ≠ n ならば Σ [Qm(i) Qn(i)] = 0となることを確認せよ。 ここでは Σ i = 0から N までの総和を取る。
9-3.等しい間隔 h で取られた N + 1 個のデータ(i h, yi)(i = 0, 1, …, N)に対し、 m 次の多項式 y(t) = a0 Q0(t/h) + a1 Q1(t/h) + … + am Qm(t/h) を最小2乗法を用いてあてはめる。 この時、係数ajが Σ [Qj(i)yj]/ Σ [(Qj(i))2]で与えられることを示せ。
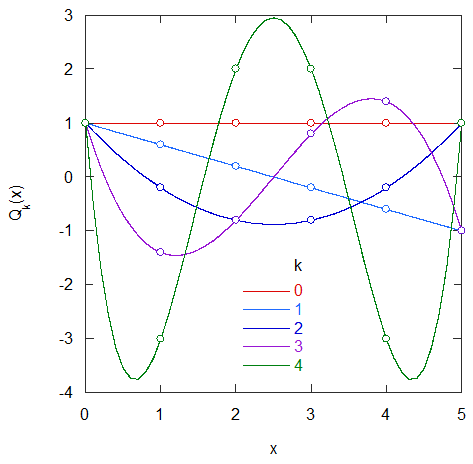
N = 5 の場合について、Q0(x)、Q1(x)、Q2(x)、Q3(x)、Q4(x) のグラフを書くと次のようになる。

N = 5 の場合について、Qk(x) の x = 0, 1, 2, 3, 4, 5 での値を計算すると下表のようになる。
| x | Q0 | Q1 | Q2 | Q3 | Q4 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0.6 | -0.2 | -1.4 | -3 |
| 2 | 1 | 0.2 | -0.8 | -0.8 | 2 |
| 3 | 1 | -0.2 | -0.8 | 0.8 | 2 |
| 4 | 1 | -0.6 | -0.2 | 1.4 | -3 |
| 5 | 1 | -1 | 1 | -1 | 1 |
どの組み合わせについても m ≠ n ならば Σ [Qm(i) Qn(i)] = 0 が満たされている。
正規方程式は次のように書ける。
\[ \left( \begin{array}{cccc} \{Q_0\}\{Q_0\} & \{Q_0\}\{Q_1\} & \cdots & \{Q_0\}\{Q_N\}\\ \{Q_1\}\{Q_0\} & \{Q_1\}\{Q_1\} & \cdots & \{Q_1\}\{Q_N\}\\ \vdots & \vdots & \ddots & \vdots\\ \{Q_N\}\{Q_0\} & \{Q_N\}\{Q_1\} & \cdots & \{Q_N\}\{Q_N\} \end{array} \right) \left( \begin{array}{c} a_0 \\ a_1 \\ \vdots \\ a_N \end{array} \right) = \left( \begin{array}{c} \{Q_0\}\{y\} \\ \{Q_1\}\{y\} \\ \vdots \\ \{Q_N\}\{y\} \end{array} \right) \]
ここで {X}{Y} は Σ [X(i) Y(i)] を表す。 m ≠ n ならば (Qm}{Qn} = 0 だから、行列は対角化され、 aj = {Qj}{y}/{Qj}{Qj} で与えられる。