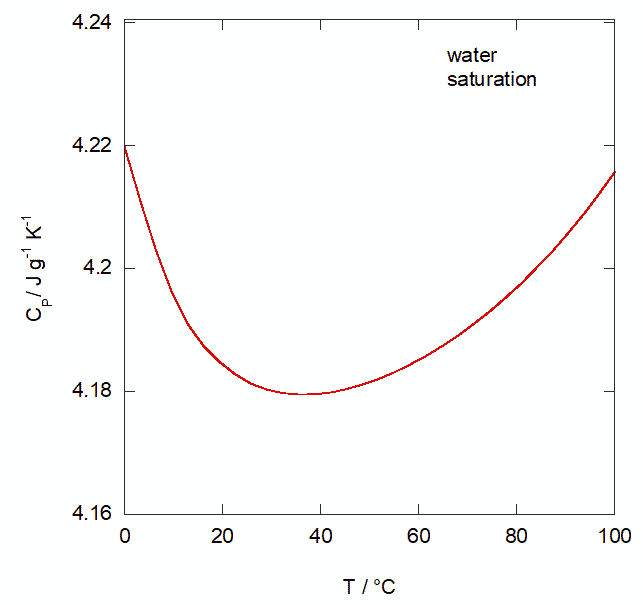
水の等圧熱容量の温度依存性
1.熱量・エネルギーの単位として、いくつかのカロリーが併用されている。 化学・食物学の分野では 1 cal = 4.184 J(熱化学カロリー。区別する時には calth と表記)が用いられるが、 4.1868 J (国際蒸気表カロリー。calIT)は電力等の分野では国際的にも用いられ、 国内では今も一部 4.18605 J (「旧計量法カロリー」 ) が生き残っている。
1-1.安息香酸の標準燃焼エンタルピー変化 ΔCH° は -3227.0 kJ mol-1であるという。 熱化学カロリー、国際蒸気表カロリーで表わすと、それぞれいくらになるか?
1-2.「旧計量法カロリー」を用いて、熱量 x cal を与えた時のあるエンジン部品の温度変化 t K が
t = 8.256 x - 0.07233 x2
で与えられていたという。「旧計量法カロリー」の代わりに熱化学カロリー y calth を用いたら、 この温度変化を与える式の係数はいくらになるか?
「旧計量法カロリー」は、もとは (1/860)× 3600 Jで提案されていた。 日本の昔の計量法(1992年に改正され今の計量法になった)が採用していたのでこの名がある。
1-1.
ΔCH° = -3227.0 kJ mol-1 = -3227.0×(kcalth/4.184) mol-1 = -771.27 kcalth mol-1
= -3227.0×(kcalIT/4.1868) mol-1 = -770.76 kcalIT mol-1
単位間の換算式を代入してもらえばよいのです。 よくある間違いは有効数字の取り方です。 3227.0/4.184 の計算を、4.184 の有効ケタを4ケタだとして 771.3 とするのは誤りです。 4.184 は定義量で誤差のない数値ですから、ここでは 3227.0 の有効ケタ 5ケタを採用して 771.27 とすることになります。
1-2.
Q = x cal = y calth
x = y (calth /cal) = y (4.184 J/4.18605 J) = 0.99951 y
より、式に代入して
t = 8.256 x - 0.07233 x2 = 8.256 × (0.99951 y) - 0.07233 × (0.99951 y)2
= 8.252 y - 0.07226 y2
物理量(Q)が数値(x あるいは y。ここでは立体で表記しています)と単位の掛け算になっていることに注意してもらえばよいのですが、
【物理量】=【数値】×【単位】
はよくても
【数値】=【物理量】/【単位】
は結構、引っかかるところです。
特にこうした「公式」という形になった時、(熱量を単位で割った)数値を代入して計算するのですが、
その数値がしばしば「熱量」と同一視されがちなことが、問題を引き起こします。
特に今回のように 0.99951 といった、ほとんど 1 ぐらいの係数がかかるようなケースでは、
当てはめて得た結果がそんなに見当違いなものにならないので、
見逃されることがあります(特に都合がよい結果が出る場合、引きずられてしまう!)。
実際にこうした練習問題をこなすことで、
問題の構図をはっきりつかんでもらうことを期待しています。
単位の換算に関わって、よく混乱のある「カロリー」を取り上げました。 化学の問題で登場するカロリーは、 何も言わなければたいてい「熱化学カロリー calth」なのですが、 それは他の分野では必ずしも通用しません。 ここには熱化学カロリー、蒸気表カロリー、(旧)計量法カロリーを取り上げましたが、 これ以外にも 15°C カロリー(cal15)なども見かけることがあります。

もともとカロリーは「水 1 gを 1 °C 温めるのに必要な熱量」~「水 1 gあたりの熱容量」です (cal15 は 14.5 °C から15.5 °C まで温めるのに必要な熱量)。 けれども水の熱容量は温度・圧力依存性を持ちます。 図には飽和水蒸気圧下の液体の水の等圧熱容量 Cp の温度依存性を示します。 水の等圧熱容量は、0 °C 付近から温度を上げていくと、 最初減少し、35 °C 付近で極小となって増大に転じます。 このため、どの温度に着目するかで話が変わってくるわけです。 さらに細かく言うと、ここでは飽和線に沿った等圧熱容量を示しましたが、 等圧線であれば若干、話が変わってきます。 たとえば飽和線に沿った10 °C の Cp は 4.1955 J g-1 K-1ですが、 1 bar での Cp は 4.1952 J g-1 K-1で若干小さくなります。 これは10 °C の水蒸気圧が 0.012 bar なので、1 barほど加圧することによって、 等圧熱容量が減少した効果を反映しています。
通常の条件下、液体の等圧熱容量は一般に圧力を上げると小さくなります。 これは(∂ CP/∂ P)T = -T (∂2 V/∂ T2)P に注意すると、 通常の液体の等圧条件での体積の温度依存性のカーブが下に凸になっていることに相当します。
さて物理化学では、こうした水の単調でない挙動に注目が集まりがちですが、 この温度範囲で変動の幅は 1 %程度。 他の液体に比べると変化量はかなり小さいのです (例えばトルエンの等圧熱容量は0 °C から100 °C まで上げると、 1.63 J g-1 K-1 から 1.96 J g-1 K-1 まで、2割ほど増加します)。 ですから実用上は、水の熱容量をほぼ一定と見なして、さほど大きな問題はおきません。 そこで細かいことには目をつぶって、 ざっくり 15 ~ 20 °C の Cp に相当する 4.184 J に切りよくしたのが、 熱化学カロリーというぐらいに思っておけばよいでしょう。 国際蒸気表カロリーなども、もともと 1/860 W h(旧計量法カロリーはこの流れをくむ)と約束していたものに、 J の定義変更にともなう若干の変更を加え、 最終、華氏温度(1 °F = (5/9) °C)との換算が簡単になるように、9 で割り切れる 4.1868 という数値にしたようです。
こうしたカロリーの定義の問題はいささかマニアックではありますが、時として大きな問題となりえます。 特に量子化学計算では、いまだにカロリーを愛用する人たちがいますが、 エネルギーをカロリーに焼き直す時、4.184 で一貫して扱っておればよいのですが、 ちょっとした手違いで一部 4.1868 を使ったりすると、 エネルギー変化の評価がとんでもないことになります。
なおここでは等圧熱容量を問題にしていますが、 水の等積熱容量 CV は、飽和線に沿って温度を上げると 300 °C ぐらいまで単調に減少します。 こういった側面も注意しておいてもらってよいでしょう (1 気圧で最大密度温度 4 °C では、 CP と CV は一致します)。