|
|
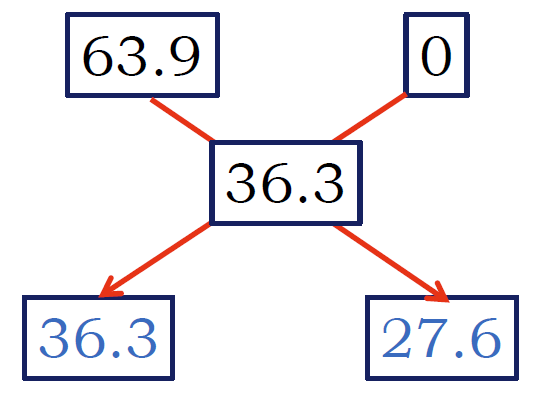
| 63.9 % 溶液(硫酸銅五水塩)と水を混ぜて 36.3%にするには、 63.9 % 溶液 (36.3 - 0) に 水 (63.9 - 36.3) を混ぜればよい。 | 36.3% を 63.9 % 溶液(硫酸銅五水塩)と14.4 %溶液に分けると、 63.9 % 溶液 (36.3 - 14.4) と 14.4 %溶液 (63.9 - 36.3) になる。 |
6.質量分率 25 %と 10 %の食塩水が用意されている。 この2つの溶液を混合して20 %の食塩水を 50 g作るには、 25 %と 10 % の食塩水をそれぞれ何 gとればよいか? また15 %の食塩水を 50 g 作るにはそれぞれ何 g とればよいか?
7.ホウ砂 Na2B4O7·10H2O の 25 °C における飽和溶液の濃度は 無水物 Na2B4O7 として質量分率 3.1 %だという。 25 °C でホウ砂 5.0 g を溶かすのに水は少なくとも何 g 必要か?
8.硫酸銅の飽和溶液の無水物 CuSO4 としての質量分率は 10 °C で 14.4 %、80 °C で 36.3 % であるという。 80 °C で硫酸銅五水和物 30 g を水に溶かして飽和溶液を作るには水が何 g 必要か? またその飽和溶液を 10 °C に冷却すると最大何 g の硫酸銅五水和物が析出するか?
質量分率 wa の溶液と、質量分率 wb の溶液を、
それぞれ質量 a、b とって混合した時にできる溶液の質量分率 w は
w = (a wa + b wb) / (a + b)
で与えられ、a と b の間には次式が成立する事に注意する(”てこの法則”)。
a / b = (w - wb) / (wa - w)
(25 - 20)/(20 - 10) = 1/2 より
25 % 食塩水と10 % 食塩水を 2:1 つまり、それぞれ 33 g と 17 gとればよい。
15 % なら混合比は 1:2 なので、25 % 食塩水 17 g と 10 % 食塩水 33 g とればよい。
ホウ砂 Na2B4O7·10H2O の式量は 381.37、 無水塩 Na2B4O7 の式量は 201.22。 ホウ砂中の無水塩の質量分率は 201.22/381.37 = 52.8 %。
ホウ砂を 52.8% の「無水塩溶液」と見なせば、 その 5.0 g に水 w を加えて 3.1% にすると考えて
(52.8 - 3.1)/(3.1 - 0) = w / (5.0 g)
より w = 80.2 g
硫酸銅五水塩 CuSO4·5H2O の式量は 249.68、 無水塩 CuSO4 の式量は 159.61。 硫酸銅五水塩中の無水塩の質量分率は 249.68/159.61 = 63.9 %。
硫酸銅五水塩 を 63.9 % の硫酸銅溶液と見なせば、 その 30 g に水 w を加えて 36.3%にするには
(63.9 - 36.3)/(36.3 - 0) = w / (30 g)
より w = 22.8 g の水を加えればよい。
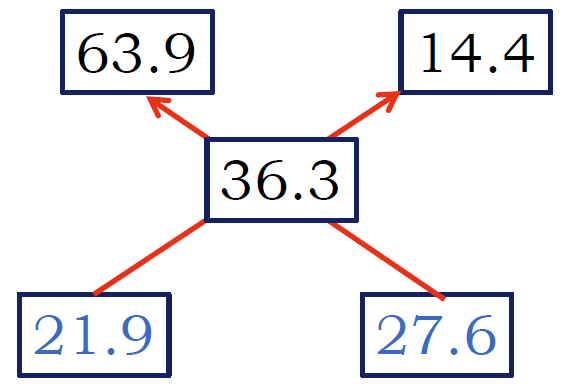
10 °C に冷却した場合には 52.8 g の硫酸銅の 36.3% 溶液が、 質量 w1 の 63.9 %溶液(= 硫酸銅五水塩)と w2 の 14.4%溶液(= 硫酸銅飽和溶液)になるわけだから
(63.9 - 36.3) / (36.3 - 14.4) = 1.243 = w2 / w1
より、析出する硫酸銅五水塩は w1 = 52.8 g/(1 + 1.243) = 23.5 g。
ここで取り上げられたのは、 実験室でごく普通に出てくる濃度調製・結晶水を含む物質の扱いです。 おそらく中学や高校(小学校でも?)の化学計算問題でも出てくるでしょう。 この解答例では敢えて“実践的”に「算数」で迫ってみました。
この種の問題を学生さんに解いてもらうと、 ほぼ全員、次のような「代数」でやってくれます。
x + y = 50
0.25 x + 0.10 y = 0.20 (x + y)
ここから 0.25 x + 0.10 (50 - x) = 0.20 × 50 = 10。
0.15 x = 5 より、x = 17。
25 % 食塩水 を 17 g、10 % 食塩水を 33 g 混ぜればよい。
「現場」ではその時の必要に応じて、こうした計算を、 調製する濃度、調製する量に対して行わなければなりません。 また結晶水を含む固体の場合には、 式自体は難しくはありませんが、 問題を式に落とし込むところで苦戦するケースが多いようです。

|

|
| 63.9 % 溶液(硫酸銅五水塩)と水を混ぜて 36.3%にするには、 63.9 % 溶液 (36.3 - 0) に 水 (63.9 - 36.3) を混ぜればよい。 | 36.3% を 63.9 % 溶液(硫酸銅五水塩)と14.4 %溶液に分けると、 63.9 % 溶液 (36.3 - 14.4) と 14.4 %溶液 (63.9 - 36.3) になる。 |
解答例に紹介する手法は「てこの法則」を使い、 パターン化したやり方で答えを導ける点で有用だと思っています。 というか、ぼくが若いころ教わったのは、 こうした方法だったと記憶しています(かなりおぼろげですが)。 今では忘れられた方法なのかもしれませんが、 ぼくは今もこうした計算をする時は、 ノートの隅に右図のような“ダイアグラム”を書いています。