|
|
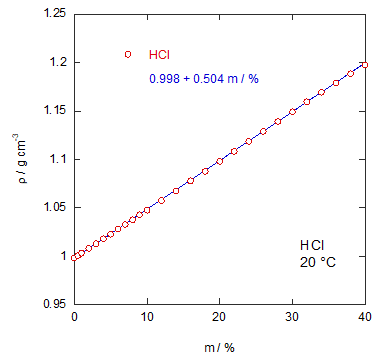
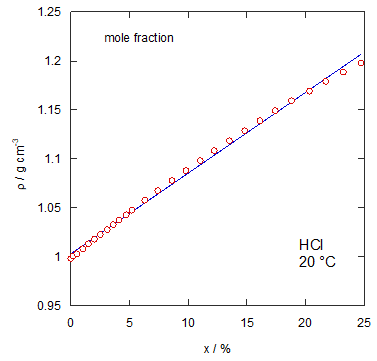
| 図1a 塩酸の密度の質量分率依存性 | 図1b 塩酸の密度のモル分率依存性。 青い実線は線形最小2乗法による |
ρ(m) / g cm-3 = 0.998 + 0.504 m
で表されるという。
9-1.質量百分率 36.0 %の塩酸の容量モル濃度を mol/L 単位で求めよ。
9-2.質量百分率 36.0 %の塩酸 200 gと水 200 g を混合すると、何 mol/L の塩酸が得られるか。 36.0 %の塩酸 200 mL と水 200 mL を混合するとどうか?
9-1.
容量モル濃度 c は
c = m ρ(m) / MW(HCl) = m (0.998 + 0.504 m) g cm-3/(36.458 g/mol)
より、m = 0.360 なので c = 11.64 mol/L。
9-2.
同質量の混合の場合、塩酸の質量分率は 18.0 %となり、上式より容量モル濃度は 5.38 mol/L。
同容量 v の混合の場合、混合してできる塩酸の質量分率 mX は
mX = [m v ρ(0.36)]/[ v ρ(0.36) + v ρ(0)] = m ρ (0.36)/[ρ (0.36) + ρ(0)]
より mX = 0.195。 上式より容量モル濃度は 5.86 mol/L。
ここで取り上げたのは、 希釈の際の容量濃度の変化です。 希釈操作の際、たとえば 10 倍希釈の時 「メスフラスコにホールピペットを用いて 10 mL精確にとり、水を加えて希釈し、精確に 100 mLにする」 といった記述があります。 混合の際の体積変化があるので、無論混合後の体積で容量を合わせないといけないわけですが、 「10 mL に水 90 mL を加えたらどうなるの?」 「10 g に水 90 g を加えたらどうなるの?」 という素朴な疑問をとりあげました。 こうした時、容量濃度は精確には 1/10 にはならないのですが、 いったいどれぐらい違うものでしょう? ここではいささか極端な例として、 濃塩酸を取り上げてみました。

|

|
| 図1a 塩酸の密度の質量分率依存性 | 図1b 塩酸の密度のモル分率依存性。 青い実線は線形最小2乗法による |
まず実際の塩酸の密度データを紹介しておきましょう(CRC Handbook のデータから)。 問題文にも書きましたが、質量分率に対してほぼ線形の依存性を示しています。 このように質量分率に対して一見単純な依存性を示すからといって、 他の濃度スケールについても単純とはいきません。 たとえばモル分率に対してプロットすると、 ちょっと見ずらいかもしれませんが、 単純な直線関係からの外れが見て取れるでしょう。 このように密度の濃度依存性は一筋縄でいかないというのが、 一つのポイントです。
ここで問題にしている容量モル濃度も同様で、 質量分率 m を 18% にした時、 容量モル濃度 c は、密度 ρ と質量分率の積に比例しますから、 この場合質量分率について2次の依存を示す項が付け加わり、 11.64 mol/L の半分の 5.82 mol/L になっらず、 5.38 mol/L と 8 %近く低いものになります。
では同じ体積の水ではどうか。 容量濃度が半分になるか計算してみると、 解答例に示したように 11.64 mol/L が 5.86 mol/L。 5.82 mol/L になるべきところが、0.7 %ぐらい高めに出ましたが、 合成実験ぐらいなら許容範囲になるでしょう。
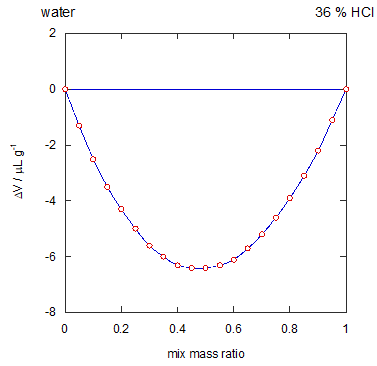
このように体積でざっくり”割った”時、 だいたい容量濃度がそれに比例して減るのは、 混合の際の体積変化が一般にあまり大きくないことによります。 図2 には 36 %塩酸と水をいろんな割合で混ぜた時の体積変化を示しました (合わせて 1 g になるように混合した時の体積変化)。 比容は 0.85 ~ 1 mL/g ぐらいですから、 体積変化としては 1/100 以下のレベルであることがわかります。 なお塩酸の場合には混合して体積の収縮が起きるのですが、 有機液体同士では一般に体積の膨張が起きることを申し添えます。
|
| 図2 36 %塩酸と水を混合した場合の体積変化。 |