1.EXCELなどの表計算ソフトには乱数を発生させる関数としてrand()が用意されており、 関数を呼び出すたびに0 ≤ x < 1となる数を等確率で与えるという。 次のような計算を行うと、どのような確率分布に従う乱数が得られるだろうか? また実際に1000個程度発生させて度数分布を計算し、予測と一致するか確認せよ。 (rand() + rand()は独立な一様乱数の和に相当することに注意)
\[ f_{\rm{Y}} (y) = \left| \frac{\rmd x}{\rmd y} \right| f_{\rm{X}} (x) \]
ここで\(x = h^{-1}(y)\)。
rand() 関数で与えられるランダム変数を \(x\) とすると、その分布関数 \(f(x)\) は次式で与えられる:
\[ f(x) = \left\{ \begin{array}{rl} 1 & 0 \le x < 1\\ 0 & \rm{otherwise} \end{array} \right. \]
与えられたランダム変数を \(y = 3 x + 1\) とする。 \(x = (y - 1)/3 \)であり、y の分布関数は x の分布関数を用いて次のように書ける:
\[ f_{\rm{Y}} (y) = \left| \frac{\rmd x}{\rmd y} \right| f (x) = \frac{1}{3} f\left(\frac{y - 1}{3} \right) \]
\(0 \le (y - 1)/3 < 1\) つまり\(1 \le y < 4\) において、右辺は1/3になる。したがって
\[ f_{\rm{Y}} (y) = \left\{ \begin{array}{cl} 1/3 & 1 \le y < 4\\ 0 & \rm{otherwise} \end{array} \right. \]
与えられたランダム変数を \(y = 2/x\) とする。 \(x = 2/y \)であり、\(y\) の分布関数は \(x\) の分布関数を用いて次のように書ける:
\[ f_{\rm{Y}} (y) = \left| \frac{\rmd x}{\rmd y} \right| f (x) = \frac{2}{y^2} f\left(\frac{2}{y} \right) \]
\(0 \le 2/y < 1\)つまり \(y > 2\)において、右辺は\(2/y^2\)になる。したがって
\[ f_{\rm{Y}} (y) = \left\{ \begin{array}{cl} 2/y^2 & y > 2\\ 0 & y \le 2 \end{array} \right. \]
与えられたランダム変数を \(y = -\ln(x)\) とする。 \(x = {\rm{e}}^{-y} \)であり、\(y\) の分布関数は \(x\) の分布関数を用いて次のように書ける:
\[ f_{\rm{Y}} (y) = \left| \frac{\rmd x}{\rmd y} \right| f (x) = {\rm{e}}^{-y} f\left({\rm{e}}^{-y} \right) \]
\(0 \le {\rm{e}}^{-y} < 1\)つまり \(y > 0\)において、右辺は\({\rm{e}}^{-y}\)になる。したがって
\[ f_{\rm{Y}} (y) = \left\{ \begin{array}{cl} {\rm{e}}^{-y} & y > 0\\ 0 & y \le 0 \end{array} \right. \]
与えられたランダム変数を \(z = x + 2 y\) として、\(x\) と \(y\) が「0, 1) の一様乱数であるとする。 \(x = z - 2y\)であり、\(y\) と \(z\) の分布関数 \(f_{\rm{Y, Z}} (y, z)\) は次のように書ける:
\[ f_{\rm{Y, Z}} (y, z) = \left| \frac{\rmd x}{\rmd z} \right| f(x) f(y) = f(z - 2y) f(y) \]

\( z\)についての分布関数を得るには、\(f_{\rm{Y, Z}} (y, z)\) を\(y\) について積分すればよい(畳み込み積分)。
\[ f_{\rm{Z}} (z) = \int {f(z - 2y) f(y) \rmd y} \]
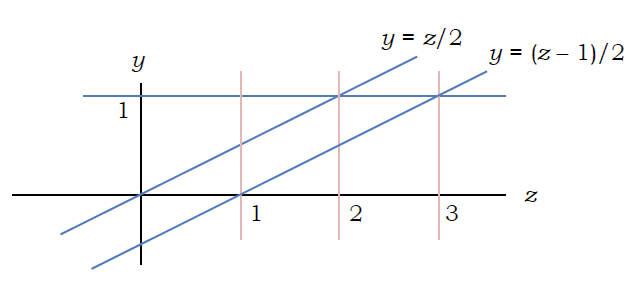
被積分関数は \(0 \le z - 2y < 1\) つまり \((z - 1)/2 < y \le z/2\) かつ \(0 \le y < 1\)となる領域で 1 となる。 これは右図で各 \(z\) に対応する位置での、当該領域の\(y\) 方向の長さを求めることに相当していて、結果は次のようになる:
\[ f_{\rm{Z}} (z) = \left\{ \begin{array}{cl} z/2 & 0 \le z < 1\\ 1/2 & 1 \le z < 2\\ (3 - z)/2 & 2 \le z < 3\\ 0 & \mbox{otherwise} \end{array} \right. \]
与えられたランダム変数を \(z = x y\) とする。 \(x = z/y\)であり、\(y\) と \(z\) の分布関数 \(f_{\rm{Y, Z}} (y, z)\) は次のように書ける:
\[ f_{\rm{Y, Z}} (y, z) = \left| \frac{\rmd x}{\rmd z} \right| f(x) f(y) = \frac{1}{y} f(z/y) f(y) \]
\( z\)についての分布関数を得るには、(4) と同様に\(f_{\rm{Y, Z}} (y, z)\) を\(y\) について積分すればよい。 \(f(z/y) f(y)\) は \(0 \le z/y < 1\) かつ \(0 \le y < 1\)、つまり \(0 \le z < y < 1\) となる領域で 1 となる。 したがって
\[ f_{\rm{Z}} (z) = \int_{z}^{1} {\frac{1}{y} \rmd y} = -\ln z \]
つまり
\[ f_{\rm{Z}} (z) = \left\{ \begin{array}{cl} - \ln z & 0 \le z < 1\\ 0 & \mbox{otherwise} \end{array} \right. \]
確率・統計に関わる事象については、中心極限定理に代表されるように、 個々に眺めると個性豊かなものでも、集団として眺めると個性が見えなくなるといった話がよく出てきます。 ここでは個々の要素は単純な分布に従うけれども、それをあるフィルターに通して眺めると複雑な挙動が見えてくるといった話題を取り上げました。
ここでも扱う、計算機で発生させることのできる単純な乱数は、一様乱数として知られるもので、 呼び出すたびに 0 から 1 の範囲の数をランダムに与えます。 たいていの言語パッケージには、組み込みで一様乱数の関数が入っています。 一様乱数の発生手法としてさまざまな手法が知られていますが、中でもMersenne Twister は優秀なようです。 なお昔の組み込みの乱数にはひどいものがあり、ぼくは流体構造に関わってひどく悩まされたことがあって、 それ以来、乱数の質は少々悪くても、自分で納得のいく、出自の知れた乱数を使うようにしています(もっぱら Knuth に紹介されていた加算合同法)。
ランダム変数を変数変換した時の分布関数(確率密度)の問題は、しばしば出会うところです。 この変換は物理量の単位の換算(変換)とも似ていて、とんでもないミスが起きることがあります。
最初の問題の \(y = 3 x + 1\) というのをとると、 \(y\) が 1 より大きく 4 までの区間で一様な乱数になるというのはたぶんいいでしょう。 ではそこでの分布関数の値というと、結構な頻度で 3 と答える学生さんがいます。 無論積分してみると、全確率が 9 になって変だというのはすぐわかるんですが、 ちょっと違和感が残ります。 分布関数というのをある微小領域 Δx 当たりの確率だとすると、それは1/Δx に比例するわけで、 Δx = (1/3) Δy ですから、Δy 当たりに直せば、3倍になってよさそうな気がします。 つまり1本100円だったら、3本300円ですよね!
ここでのポイントは、ここで考えている変数変換というのが、以前の「物理量」「単位」という文脈で言うと、 単位ではなく、物理量(ここでは領域の大きさ)自身の変換に相当しているというところでしょう。 つまり同じ量のものが、3 倍の領域に分散しているので1/3 になってしまうというわけです。 先の例でいうと、1箱3個入りのチョコトリュフが300円だったのを、個包装にして100円にした(実際にはこうはならないでしょうが)ようなものです。 このあたりの事情を「確率の保存」などと称して、 ぼくなどはよく \(f_{\rm{X}} (x) |\rmd x| = f_{\rm{Y}} (y) |\rmd y| \) などと書くのですが、 たぶん積率分布関数(数学の人たちはこれをもっぱら「分布関数」と呼ぶようです)で書いた方が自然でしょうね。
\[ F_{\rm{Y}} (y) = \int_{-\infty}^{y} {f_{\rm{Y}}(y) \rmd y} = \int_{-\infty}^{(y-1)/3} {f_{\rm{X}}(x) \rmd x} = F_{\rm{X}} \left(\frac{y - 1}{3} \right) \]
が成立するので、これを微分して(上の解答例では \(f(x) = f_{\rm{X}}(x) \) としています)
\[ f_{\rm{Y}}(y) = \frac{\rmd F_{\rm{Y}} (y)}{\rmd y} = \frac{\rmd}{\rmd y} F_{\rm{X}} \left(\frac{y - 1}{3} \right) = \frac{1} {3} f_{\rm{X}} \left(\frac{y - 1}{3} \right) \]
という次第です。 また問 (2) で逆数を取った場合に、\(1/x^2\) 項が加わるのは、 発光スペクトルなどの波長と波数の変換にともなってよく生じるので、 記憶しておいていただきたいところです。
ここでのもう一つの問題は、多変数の確率分布を1変数の分布関数にまとめた時にどうなるかということです。 簡単のため2変数の場合について考えると、 2変数の確率分布関数 \(f_{\rm{X, Y}} (x, y) \) を \(y\) についての制限を外して、 \(x\) についての分布関数にしたければ \(y\) について、全領域について積分すればよいのです。
\[ f_{\rm{X}}(x) = \int_{-\infty}^{\infty} \rmd y f_{\rm{X, Y}} (x, y) \]
積率分布関数で書けば、\(F_{\rm{X}}(x) = F_{\rm{X, Y}}(x, \infty)\) になります。 \(x\), \(y\) 別々に考えているときは簡単なのですが、問題になるのはある制約が課されている場合です。 上の問題 (4) では、\(x + 2y\) がある値\(z\)になるという確率を考えています。 解答例では分布関数で考え、畳み込み積分に持ち込んだのですが(ここでカッコよくデルタ関数を使ってみるのもアリです)、 これを積率分布関数で書けば \(x + 2y < z\) となる確率を求める問題になります。
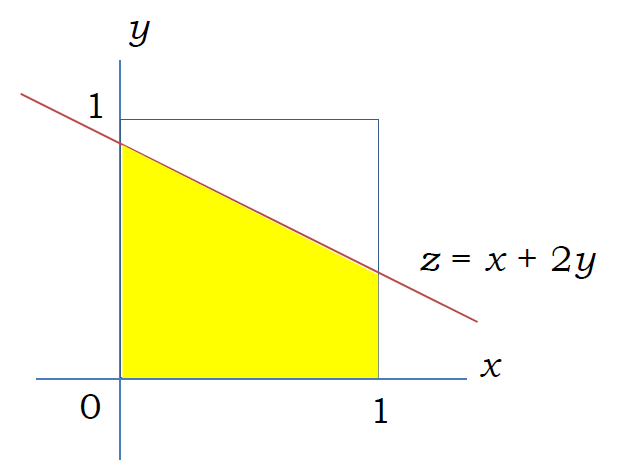
\[ F_{\rm{Z}}(z) = \int \int_{x + 2y < z} \rmd x \rmd y f_{\rm{X, Y}} (x, y) \]
\(f_{\rm{X, Y}}(x, y)\) は、\(0 \le x \lt 1, ~0 \le y \lt 1\) で 1 になるので、 この積分は右図の黄色く塗った領域の面積を求める問題に相当します。 また \(z\) の分布関数は、\(x + 2y = z\) の直線が、 原点に頂点を置く一辺 1 の正方形と交わる部分の長さ(を\(\sqrt{5}\) で割ったもの)に相当することになります。
変数変換と多変数の分布の縮約で、 一様乱数から指数分布や対数分布に従う乱数を発生させることができることを紹介したわけですが、 他にもいろんな分布に従う乱数を発生させる手法があります。 実用的に重要なのはガウス(正規)分布に従う乱数ですが、次の手法は有名です(Box-Muller 法):
\[ NR = \sqrt{-2 \ln({\rm{rand()}})} \cos(2 \pi {\rm{rand()}}) \]
この手法は 2 次元のガウス分布が、 極座標系で書くと指数分布に焼き直せることに注意すると導けます。
\[ \frac{1}{2 \pi} \exp(-x^2/2) \exp(-y^2/2) \rmd x \rmd y = \frac{1}{2 \pi} \exp(-r^2/2) r \rmd r \rmd \theta = \frac{1}{4 \pi} \exp(-s/2) \rmd s \rmd \theta \]
この言わんとするところは \((x, y)\) 平面上で、 動径方向の距離の2乗 \(s\) が指数分布に従う、等方的なベクトルの \((x, y)\) 成分は、 ガウス分布に従うということです。 上の問(3) で見たように -ln(rand()) は指数分布に従います。 また (cos(2 π rand()), sin(2 π rand())) (ここでrand()は同一の一様乱数)は、 等方的な単位ベクトルになりますから、 先の \(NR\) の式で得られる乱数が、ガウス分布に従うことがわかるでしょう。
他にもさまざまな分布に従う乱数を発生させる手法がありますが、 そうした手法を詳細に取り上げた本に L. Devroye, "Non-Uniform Random Variate Generation," Springer, 1986 があります (著者のサイトから読むことができます)。 困ったときには眺めてみるといいでしょう。