2020.4
吉村洋介
化学実験法II 問題集
統計・検定・不確かさ
実験で実際に出会うような、
統計、検定、誤差にかかわるような問題を集めてみました。
1.EXCELなどの表計算ソフトには乱数を発生させる関数としてrand()が用意されており、
関数を呼び出すたびに0 ≤ x < 1となる数を等確率で与えるという。
次のような計算を行うと、どのような確率分布に従う乱数が得られるだろうか?
また実際に1000個程度発生させて度数分布を計算し、予測と一致するか確認せよ。
(rand() + rand()は独立な一様乱数の和に相当することに注意)
- (1) 3*rand() + 1
- (2) 2/rand()
- (3) -ln(rand())
- (4) rand() + 2*rand()
- (5) rand()*rand()
2.x と y を平均と分散が等しい独立なランダム変数で、平均を μ 分散を σ2 とする。
次の(共)分散を μ と σで表せ。
- (1) ⟨⟨ x + 3, x - 3 ⟩⟩
- (2) ⟨⟨ x + y - 2μ, x + 3y ⟩⟩
- (3) ⟨⟨ x + y, x - y ⟩⟩
- (4) ⟨⟨ xy, xy ⟩⟩
⟨⟨p, q⟩⟩ ≡ ⟨p q⟩ - ⟨p⟩ ⟨q⟩ で、p と q の共分散。
文脈で誤解がなければ、⟨⟨p, q⟩⟩ を ⟨⟨pq⟩⟩ と表記することがある。
⟨⟨x, x⟩⟩ = ⟨⟨x2⟩⟩ = σ2。
3.4回の測定で得た測定値 \(x_1, x_2, x_3, x_4\) の残差2乗和 \(S\) について問いに答えよ。
3-1.\(S = a [(x_1 - x_2)^2 + (x_2 - x_3)^2 + (x_3 - x_1)^2] + b (3x_4 - x_1 - x_2 - x_3)^2\) と表したとき、\(a, b\) はそれぞれいくらか?
3-2.\(S = a (x_1 - x_2)^2 + b (2x_3 - x_1 - x_2)^2 + c(3x_4 - x_1 - x_2 - x_3)^2\) と表すことができる。
\(a, b, c\) はそれぞれいくらか?
4.銅の含量41.2 %と書かれている黄銅(真鍮)の板がある。この板の銅の含量 x %を10人の優秀なK大学の学生が分析し、
xとしてそれぞれ以下の結果を得た:
40.3, 40.6, 41.1, 40.8, 40.5, 41.0, 41.3, 40.8, 41.0, 40.7
4-1. 学生の分析値 x の標本平均と標本標準偏差を求めよ。
4-2. 学生の分析値 x の標準偏差が 4-1 で求めた標本標準偏差に等しいとする。
黄銅の板の銅の含量を 41.2 %と見なしてよいかどうか、
正規分布を仮定して有意水準5 %で判定せよ。
また標準偏差を仮定せず t検定を用いたらどうか?
5.銅の合金中の亜鉛の組成を調べるのに、容量分析による方法と重量分析による方法がある。
優秀なK大学の学生が、ある合金サンプルを容量分析と重量分析で分析して亜鉛の質量百分率w %を求めたところ、
容量分析の測定件数 43件 でwの標本平均は 26.17 で標本標準偏差 0.83、
重量分析は測定件数 25件 で標本平均 26.32 で標本標準偏差 0.88 であったという。
5-1. 容量分析と重量分析の分析値の分散が同じと見なせるかどうかを、F 検定を用い有意水準 5 %で判定せよ。
5-2. 容量分析と重量分析の分析値の分散が等しくσ2であるとする。
容量分析と重量分析の分析値の標本平均値の差の分散が σ2 [(1/43) + (1/25)]になることを、教員に分かる程度に説明せよ。
5-3. 容量分析と重量分析の w の標本平均の差が、
有意水準5 %で有意であるかどうかを t-分布を用いて判定せよ。
容量分析と重量分析の分析値の分散は等しいとする。
6.【2018年度試験問題から】以下の文章を読み問いに答えよ。
Uくんが試験に出るかもしれないと、次の問題を解こうとしていると、
横から Y と Hくんがのぞき込んで議論が始まり、そこに大先輩の Q 先生がやってきた:
10 kgの米の入った袋に、米粒の平均の重さが25.0 mgであると表示されていた。
このことを確かめるために袋から米粒を10 粒取り出し、
一粒ずつ重さをはかったところ平均が23.5 mg、
標本標準偏差が2.0 mgだった。
この結果から5%の有意水準で表示が間違っているといえるかどうか判断せよ。
- Y:米粒の重さの平均が25.0 mg、分散が σ2 であるとしよう(H0)。
10粒の標本平均と25.0 mgの差は平均 0 分散 イ の正規分布に従うと考えられ、
その2乗(2.25 mg2)を イ で割ったものは自由度 の χ2分布に従う。
また標本分散((2.0 mg)2 = 4.0 mg2)を ロ で割ったものは
自由度 ハ の χ2分布に従う。
(1) z = 22.5/4.0 = 5.6は自由度( ロ , ニ ) の F 分布の上側(右側)2.5%点7.209より小さく、
この10粒の測定からは、有意水準5 %で米粒の重さの平均が25.0 mgでないとはいえない。
- H:これは t 分布を使うんだよ。t = (23.5 - 25.0)/(2.0/\(\sqrt{10}\) ) = -2.37 でこれは自由度 ホ の t 分布の下側(左側)2.5%点の -2.262より小さい。
だから有意水準5 %で米粒の重さの平均が25.0 mgであるとはいえない。
これが答えだよ。
- U:でどちらが正解なの?やっぱり呆けの来ているYではなく、Hくんだよね。
- Q:Y君の考えも彼らしく最後のところで残念なことになっているが、まったく間違っているわけでもないよ。
Y君のやり方では有意水準が ヘ %になる。
(2) 棄却域の設定に当たって、F分布の上側 5 %点 5.117を取る必要があり、
5.6は棄却域に入っているから、t分布を使った評価同様、有意水準5 %で米粒の重さの平均が25.0 mgであるとはいえない。
両者は同等なんだよ。
Y君の計算した z とHくんの求めた t とは z = t2 の関係にあり、
(3) 一般に自由度( ロ , f )のF分布の上側5 %点は自由度 f の t分布の下側(あるいは上側)2.5 %点の2乗に等しい。
Y君も及ばずながら何とか論理を構築しようと努力していることには、もっと敬意を払うべきだと思う。
理学部的にはU君、君が不正解だよ。
6-1.文中の イ~ヘに当てはまる適切な数字・数式を記せ。
6-2.Yの論旨に沿って、下線部 (1) で計算される z が自由度 ( ロ , ニ )のF分布に従うと考えられることを示せ。
6-3.Q先生の説明の下線部 (2) で、なぜ棄却域を両側に取らず片側に取るのか、
対立仮説H1の下で H0 の棄却率を最大化する立場から、
教員(Yの方)にも分かるように説明せよ。
6-4.標準正規分布に従う変数 u と自由度 f の χ2 分布に従う変数 vf を取った時、
u/\(\sqrt{v_{\rm{f}}/f}\) が自由度 f の t分布に従うことに注意して、
下線部 (3) が成り立つことを教員(Yの方)にも分かるように説明せよ。
7.溶液中の塩化物イオンを硝酸銀による滴定で定量する際、滴定終点を定めるのにMohr法とFajans法がよく用いられる。
表に示すのは、K大学の優秀な学生たちが、同じ海水希釈液中の塩化物イオンの濃度x mmol/LをMohr法とFajans法で測った結果である。
| 学生番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mohr | 55.7 | 55.8 | 53.1 | 54.0 | 55.2 | 52.9 | 54.7 | 54.4 | 54.2 | 53.9 |
| Fajans | 52.8 | 53.5 | 53.1 | 53.9 | 53.8 | 52.9 | 53.3 | 53.0 | 52.6 | 53.0 |
| 学生番号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Mohr | 54.8 | 54.2 | 54.9 | 55.2 | 55.1 | 53.9 | 55.1 | 52.9 | 55.3 | 56.2 |
| Fajans | 53.1 | 52.5 | 54.1 | 53.8 | 54.1 | 53.0 | 53.8 | 52.9 | 53.4 | 53.5 |
7-1.Mohr法 と Fajans法で決めた濃度の標本分散の比は F分布に従うと考えられる。
F分布を用いてMohr法とFajans法で分散に差異があるかどうかを有意水準5 %で判定せよ。
7-2.2つの統計集団の分散が異なる時、両者の平均の差異を統計的に厳密に扱うことは困難である。
一人一人の学生について、Mohr法とFajans法で得られた結果の差 d を取りこれに t-検定を適用してMohr法とFajans法で得られる分析値に差異があるかどうかを判定せよ
(「対応のあるt-検定」あるいは「対に対するt-検定」などと呼ばれる)。
8.JIS規格に定められているホールピペットの許容誤差は、
ピペットの容量が10 mLであれば0.02 mL、20 mLであれば0.03 mLである(JIS R3505)。
市販の10 mLピペットを2回用いて20 mL測り取るのと、20 mLのピペットを用い1回で測り取るのとでは、
誤差はどちらが大きいだろうか。
9.EXCELの乱数を発生させる関数 rand() を用いて一様乱数3個からなるデータ \((x_1, x_2, x_3)\) を1000回発生させ、
標本平均とメディアン(中央値)の平均と分散を求める数値実験を行った。
この実験についての昭和の無能老人 Y と U くんの会話を読み問いに答えよ。
- Y: 関数 rand()は 0 ≤ x < 1の一様乱数を与えるので、その平均 \(\langle x \rangle\) は イ で
分散 \(\langle \langle x^2 \rangle \rangle\) は ロ だ。
これを3個とった標本平均 \(\bar{x}\) の平均 \(\langle \bar{x} \rangle\) は ハ で
分散 \(\langle \langle \bar{x}^2 \rangle \rangle\) は ニ になる。
メディアン \(\hat{x}\) は3個とった真ん中の数なわけだから、
[1/3, 2/3) の一様乱数としてふるまうだろう。
だからメディアンの平均 \(\langle \hat{x} \rangle\) は ホ で
分散 \(\langle \langle \hat{x}^2 \rangle \rangle\) は ヘ になる。
- U: 標本平均の方はいいけど、メディアンの分散はそんなに単純にはいかないよ。
メディアン \(\hat{x}\) が \(y ~(0 \le y \lt 1) \) より小さい確率 \(F(y)\) を考えると、
それは \((x_1, x_2, x_3)\) の内2個以上が \(y\) 未満の確率だ。
rand() 関数が \(y\) より小さい値になる確率は \(y\) に他ならないから、
\((x_1, x_2, x_3)\) がすべて \(y\) 以下の確率と、
\((x_1, x_2, x_3)\) の内2つが \(y\) 以下で1つが \(y\) 以上の確率を足して、
ト になる。
だからメディアン \(\hat{x}\) の分布関数 \(f(y)\) は チ になるはずだ。
ここからメディアンの平均 \(\langle \hat{x} \rangle\) は リ で
分散 \(\langle \langle \hat{x}^2 \rangle \rangle\) は ヌ になる。
9-1.文中の イ~ヌに当てはまる適切な数・数式を記せ。
9-2.実際に数値実験を行って、標本平均とメディアンの平均と分散を求め、Uくんの評価と一致するかどうか確認せよ。
10.F分布とt分布について次のことを検討せよ。
10-1.x = F(φ1, φ2; P) は F分布に従うランダム変数が x 以上の値を取る確率が P であることを示す(F分布の積率分布関数の逆関数相当)。
φ1は分子、φ1は分母の自由度に対応する。
F(φ1, φ2; P) = 1/F(φ2, φ1; 1 - P) であることを示せ。
また実際に表計算ソフト等で F(20, 30; 0.025) を計算し(EXCELであれば F.INV.RT(0.025,20,30))、
この関係が成り立っていることを確認せよ。
10-2.x = t(φ; P) は自由度 φ の t分布に従うランダム変数の絶対値が x 以上の値を取る確率が P であることを示す。
[t(φ; P)]2 = F(1, φ; P)であることを示せ。
また実際に t(20; 0.05) と F(1, 20; 0.05) の計算値を比較してこの関係が成り立っていることを確認せよ
(EXCELであれば T.INV.2T(0.05,20) と F.INV.RT(0.05,1,20) を比較検討すればよい)。
11.【2014年度試験問題から】N神社の御手洗の水の硬度(ここではカルシウムとマグネシウムの合量の濃度で表示)x μmol/Lを、K大学の優秀な3回生が毎年キレート滴定で測っている。
2010年度は14件が、2014年度は19件の測定値が得られ(外れ値outlierは省いてある)、
2010年の x の標本平均は 276 で標本標準偏差18、2014年の標本平均は 246 で標本標準偏差 23 であったという。
このデータを解析した U 君の次の文章を読み、問いに答えよ。
まず 14 年度と 10 年度で測定値のばらつき、分散が同じと見なせるかどうかを検討しよう。
14 年度と10 年度の標本分散の比は (23/18)
2 = 1.63である。
一見 14年度の学生の測定の精度が低そうに見える。
しかし統計的な検定の立場に立つとそうでもない。
もし分散が等しいとすれば、これは自由度 (φ
1, φ
2) = (
イ ,
ロ )の F 分布に従うはずで、
F(
イ ,
ロ ; 0.025) = 3.0 なので、
有意水準 5 %で両者の分散は同じと見なしていいだろう。
以下では10年度と14年度の測定値の分散が等しく σ
2 であるとする。
10年度と 14年度の標本分散を用いて、σ2 は s2 = (13×182 + 18×232)/31 で推定できる。
10年度の標本平均の分散は ハ σ2、
14年度の標本平均の分散は ニ σ2である。
さて 10年度と 14年度の測定値の平均が等しいものとすれば、10年度と14年度の標本平均の差の2乗を ホ σ2 で割ったものは、
自由度 1 の χ 2 分布に従う。
一方 ヘ s2/σ2は自由度 ト のχ2 分布に従うと考えられる。
つまり標本平均の差の2乗 (246 - 276)2 を チ s2で割ったものは、
自由度が (φ1, φ2) = ( リ , ヌ )のF分布に従う。
F( リ , ヌ ; 0.05) = 4.2なので、有意水準 5 %で標本平均が等しいと {A: 見なせない、見なせる}。
つまり 10年度と 14年度で、採水したN神社の水の硬度に変化があったと {B: 考えられない、考えられる}。
11-1. 文中のイ~ヌに当てはまる適切な数値・数式を記し、{ A }、{ B }については適切な語を選べ。
11-2. U君はF分布を用いて10年度と14年度の測定値の平均値が同じかどうかを検定したが、
t分布を用いることもできる。
測定値の平均が等しいとすれば、標本平均の差 246 - 276 を ホ 1/2 s で割ったものは自由度 ヌ の t分布に従うことを説明せよ。
12.[2017 年度の問題] K大学の学生実験室では、常備している70本のホールピペットが年間8本ぐらいのペースで破損し適宜補充しているという。
ホールピペットの寿命についての次のSくんと無能の昭和老人YYの会話について に適切な式・数値を入れよ。
- YY: 1993年以前はホールピペットに検定証印(
 。1992年改正前の計量法では、ホールピペットは国の検定を受けていた)が付いていたが、
93年以降なくなった。毎年8本ずつ消えていったとして、2003年ごろにはなくなったわけだね。
。1992年改正前の計量法では、ホールピペットは国の検定を受けていた)が付いていたが、
93年以降なくなった。毎年8本ずつ消えていったとして、2003年ごろにはなくなったわけだね。
- S: 話が違うよね。毎年全体のa = 8/70ずつ消えていくということは、
毎年全体の (1 - a) だけ残っているということだから、t 年後には イ 残っていることになる。
指数関数で近似すれば ロ だ。
23 年たった今でも、70本の内 5本ぐらいには検定証印が残ってるんじゃないかな。
- YY: 言われてみると見た気がするね。
ところで生き残ってるのが ロ だとすると、ピペットの平均寿命は、ちょうど半分壊れるころ ロ = 0.5だから 6 年ぐらいということだね。
- S: それはメディアン(中央値)だよ。t 年目に壊れる確率は ハ で与えられるから、平均寿命は ニ 年ぐらいじゃないかな。
13.[2017 年度の問題] K大学の優秀な学生たちは、簡易屈折率計PAL-RIを用いた混合溶液の濃度決定にここ数年取り組み、
濃度を知らされていない覆面試料の濃度決定を行っている。
溶液はシクロヘキサン-トルエン混合溶液で、その濃度 x %に対し、2015 年度と2016 年度の結果は下表のとおりであったという。
| 調製濃度/% | 測定チーム数 | 標本平均 | 標本標準偏差 |
| 2015年度 | 66.39 | 25 | 66.75 | 1.59 |
| 2016年度 | 34.45 | 18 | 33.39 | 2.11 |
13-1.2015年度、2016年度それぞれについて、簡易屈折率計で決めた濃度が、真の濃度(調製濃度)と一致すると考えてよいかどうかを有意水準5%で判定せよ。
13-2.2015年度と2016年度で、学生の結果のばらつきが異なっていると見なせるか有意水準5%で判定せよ。
14.濃度 cHCl の塩酸の標定を、濃度 cOx のシュウ酸溶液を標準にして、
BTBを指示薬に濃度 cNaOH の水酸化ナトリウム溶液を用いて行なった。
シュウ酸溶液、塩酸をそれぞれ容量 V の同じホールピペットを用いて採取し、
シュウ酸溶液については v1、塩酸についてはv2の滴定値を得たという。
(濃度はすべて物質量の濃度)
この標定操作から得られる塩酸濃度 cHCl の誤差について、
滴定値 v1 と v2 の誤差の影響を解析した以下の文章を読み、問いに答えよ。
それぞれの滴定結果から、シュウ酸は二塩基酸なので塩酸濃度は次式で与えられる:
cHCl = イ
塩酸濃度の精確な値c°
HCl からの偏差 δc
HCl (= c
HCl - c°
HCl )は、
精確な当量点からの滴定値の偏差 δv
1、 δv
2 が十分小さければ
δcHCl = ( ∂cHCl/ ∂v1) δv1 +(∂cHCl/∂v2) δv2
より:
δcHCl / cHCl = ロ δv1 + ハ δv2
この滴定操作では、溶液の色が黄色から緑になったところを終点とする。
変色が確認できた時点での滴下量を読み取るので、変色が十分鋭敏に起きるなら平均的に見て一回に滴下する容量 v
X の半分だけ入れすぎてしまう。
また分散は v
X2/12と評価される。
したがって滴定値の偏差が、この終点の判定にともなう偏差によるものとすれば、
計算される塩酸濃度の偏差の平均 ⟨ δc
HCl⟩
と分散 ⟨⟨c
HCl2⟩⟩ は次式で表わされる:
⟨ δcHCl⟩ = ニ cHCl
⟨⟨ cHCl2⟩⟩ = ホ cHCl2
14-1.文中イ~ホに適切な式を記せ。
14-2.0.0500 mol/Lのシュウ酸溶液を標準物質にして、
上記の標定操作を行いシュウ酸については 10.10 mL、塩酸については 9.50 mL の滴定値を得たという。
一回に滴下する容量 vX = 0.030 mLとして、
上記の誤差解析に基づき、得られる塩酸濃度の精確な濃度からの偏差の平均値と標準偏差を求めよ。
14-3.用いたのが 10 mLのホールピペットで、
採取する容量の標準偏差が 0.010 mLであったとする。
このことを考慮した時、上で求めた塩酸濃度の標準偏差はどうなるか?
15.市販の乳酸(C3H6O3。分子量90.08)は一部縮合してエステルを生成しており、
一端水酸化ナトリウム溶液を加えてエステルを加水分解した後、過剰の水酸化ナトリウム量を逆滴定することで総乳酸量を決定する。
これに従い、実際に次の実験を行った:
市販乳酸を49.9 mass%に希釈した溶液を0.3731 g 取り、
加水分解のために 0.2 mol/L の水酸化ナトリウム溶液を 18.10 mL加えて加熱した。
加水分解後に 0.2008 mol/L 塩酸でフェノールフタレインを指示薬に滴定したところ 7.38 mLを要した。
一方加水分解に用いた水酸化ナトリウム溶液 10 mLをホールピペットを用いて精確に取り、
同様に 0.2008 mol/L塩酸で滴定したところ 9.26 mLを要した。
15-1.滴定操作において、常に1滴 0.04 mLずつ滴下していったものとしよう。
フェノールフタレインの変色が十分鋭敏であれば、滴下後少しでも当量点 Ve mLを超えれば滴定終点 Vt mLとして判定される。
実験的に求められる滴定終点と当量点の差 Vt - Ve の平均と標準偏差はいくらになると考えられるか。
15-2. 塩酸で水酸化ナトリウムを滴定する際の誤差が上に示したように評価され、
その他の誤差(測容器の誤差、乳酸希釈度、塩酸濃度の標定誤差等)は無視できるほど小さいとしよう。
実験結果から市販乳酸中の総乳酸比率を求め、その誤差を評価せよ。
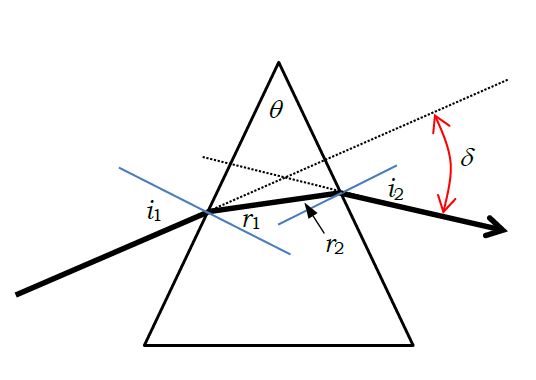
16.右図のように屈折率 n のガラスでできた頂角 θ のプリズムに、入射角 i1 を変えて光を入射させ、
入射光の偏角 δ を測定した。スネル Snell の法則から
n = sin i1/sin r1 = sin i2/sin r2
が成り立つことに注意して問いに答えよ。
16-1. δ = (i1 - r1) + (i2 - r2)、
r1 + r2 = θ となることを示せ。
16-2. 偏角の最小値(最小偏角)を δ0とすると、屈折率 n が次式で表されることを示せ。
n = sin [(θ + δ0)/2] / sin (θ/2)
16-3. 実際に測定したところ、頂角θ が60°10’ ± 3’、最小偏角 δ0が47°36’ ± 5’であったという(±は標準偏差)。
ガラスの屈折率と誤差を評価せよ。
17.ある鋼板で作った内径 D mmのシリンダーの耐圧を Pa atmにするには、
鋼板の厚さ tm mmは少なくとも
tm = Pa D/(3000 + 0.800 Pa)
でないといけないとする。
圧力が atm ではなく MPa 単位で PM MPaとして与えられたとき、
公式の係数 3000 と 0.800 はそれぞれいくらになるか。
1 atm = 0.101325 MPaである。係数はいずれも有効数字3ケタで与えるものとする。
18.物体 Q1、Q2、Q3 の重さ m1、m2、m3 を天秤で測定する。
天秤の測定値のばらつき δ の平均は 0 で標準偏差は σ であるとする。
この時、物体 Q1、Q2、Q3 を2つずつ同時にとって、
3回の秤量で下記3種類の秤量値 w1、w2、w3 を得たとしよう(δ は測定の際のばらつき)。
w1 = m1 + m2 + δ1
w2 = m2 + m3 + δ2
w3 = m3 + m1 + δ3
w1、w2、w3 から m1、m2、m3 を
m1 = (w1 + w3 - w2)/2といった関係式で得るとしたとき、
得られるm1(あるいは m2 または m3)の測定値の標準偏差はいくらになるか?
表紙のページへ
 。1992年改正前の計量法では、ホールピペットは国の検定を受けていた)が付いていたが、
93年以降なくなった。毎年8本ずつ消えていったとして、2003年ごろにはなくなったわけだね。
。1992年改正前の計量法では、ホールピペットは国の検定を受けていた)が付いていたが、
93年以降なくなった。毎年8本ずつ消えていったとして、2003年ごろにはなくなったわけだね。