問 16

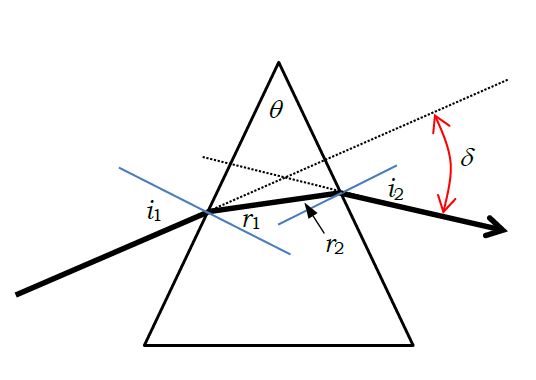
16．右図のように屈折率 n のガラスでできた頂角 θ のプリズムに、入射角 i₁ を変えて光を入射させ、 入射光の偏角 δ を測定した。スネル Snell の法則から

n = sin i₁/sin r₁ = sin i₂/sin r₂

が成り立つことに注意して問いに答えよ。

16-1. δ = (i₁ - r₁) + (i₂ - r₂)、 r₁ + r₂ = θ となることを示せ。

16-2. 偏角の最小値（最小偏角）を δ₀とすると、屈折率 n が次式で表されることを示せ。

n = sin [(θ + δ₀)/2] / sin (θ/2)

16-3. 実際に測定したところ、頂角θ が60°10’ ± 3’、最小偏角 δ₀が47°36’ ± 5’であったという（±は標準偏差）。 ガラスの屈折率と誤差を評価せよ。

解答例

16-1

δ は △ABCの ∠Aの外角なので

δ = ∠B + ∠C = (i₁ - r₁) + (i₂ - r₂)

□PBDCに注目すると、∠P + ∠D = 2∠Rであり、また△DBCに注目すると、∠D + (r₁ + r₂) = 2∠Rであるから、

∠P = θ = r₁ + r₂

16-2

入射角と屈折角の間の関係（スネルの法則） \(n = \sin i / \sin r\) から一般に

\[ n \cos r \frac{\rmd r}{\rmd i} = \cos i \]

δ = (i₁ - r₁) + (i₂ - r₂) = (i₁ + i₂) - θ に注意して、δ が最小となるとき

\[ \frac{\rmd \delta}{\rmd i_1} = 1 + \frac{i_2}{i_1} = 1 + \frac{\rmd r_1}{\rmd i_1} \frac{\rmd r_2}{\rmd r_1} \frac{\rmd i_2}{\rmd r_2} = 1 + \frac{\cos i_1}{n \cos r_1} (-1) \frac{n \cos r_2}{\cos i_2} = 0 \]

したがって

\[ \frac{\cos i_1}{\cos r_1} = \frac{\cos i_2}{\cos r_2} = c \]

とすると Snell の法則から

\[ \cos^2 r_1 = \cos^2 r_2 = (n^2 - 1)/(n^2 - c^2) \]

したがって最小偏角 δ₀において次式が成立

\[ r_1 = r_2 = \theta /2\\ i_1 = i_2 = (\theta + \delta_0)/2 \]

したがってスネルの法則から

\[ n = \frac{\sin i_1}{\sin r_1}= \frac{\sin(\theta + \delta_0)/2}{\sin(\theta/2)} \]

16-3

\[ n = \frac{\sin(\theta + \delta_0)/2}{\sin(\theta/2)} = \frac{\sin (x + y)}{\sin x} \]

とする。 角度をラジアンに換算すると x = 0.525053 ± (4.4 × 10^-4) rad、 y = 0.415388 ± (7.2 × 10^-4) rad。

\[ \frac{\rmd n}{\rmd x} = -\frac{\cos(x + y)}{\sin x} + n \frac{\cos x}{\sin x} = 1.606\\ \frac{\rmd n}{\rmd y} = -\frac{\cos(x + y)}{\sin x} = -1.176\\ \]

より、誤差の伝搬則によって屈折率の分散は

\[ \left( \frac{\rmd n}{\rmd x} \right)^2 (4.4 \times 10^{-4})^2 + \left( \frac{\rmd n}{\rmd y} \right)^2 (7.2 \times 10^{-4})^2 = 1.22 \times 10^{-6} \]

n = 1.6116 ± 1.1 × 10^-3