
10.一般に流体系での拡散には、対流が大きな役割を果たす。
\[ J_{\rm{B}} = j_{\rm{B}} + n_{\rm{B}} ~~~ \mbox{(a)} \]
狭義の拡散流速 \(j_{\rm{B}}\) はフィックの法則から次式で表され\[ j_{\rm{B}} = - D \frac{\partial c_{\rm{B}}}{\partial z} ~~~ \mbox{(b)} \]
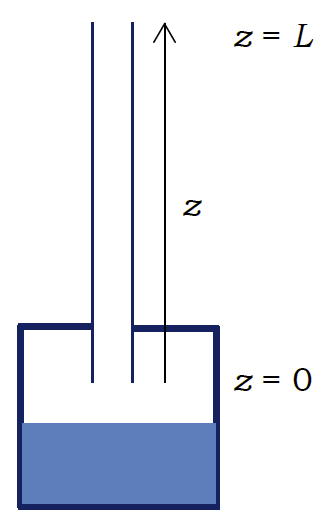
対流による拡散流速\(n_{\rm{B}}\)は、巨視的な流速\(u\)にエーテル濃度\(c_{\rm{B}}\)をかけたもの\(u c_{\rm{B}}\)に等しい。 ここで問題は巨視的な流速 \(u\) であるが、定常的な拡散なので空気Aの流れは存在しないはずで、 巨視的な流速\(u\)は、広義のエーテル拡散流束 \(J_{\rm{B}}\) によって引き起こされる巨視的な流れの速度に等しく、次式が成り立つ:\[ u = \frac{1}{c_{\rm{A}} + c_{\rm{B}}} J_{\rm{B}} ~~~ \mbox{(c)} \]
管内の圧力 \(P\) ・温度 \(T\) は一定と考えられるので、空気とエーテルの濃度の和 \(c_{\rm{A}} + c_{\rm{B}} = P/RT = c\) は一定であり(\(R\) は気体定数)、 エーテルのモル分率を \(x (= c_{\rm{B}}/c) \) とすると広義のエーテル拡散流束 \(J_{\rm{B}}\)について次式が成り立つ\[ J_{\rm{B}} (1 - x) = - D c \frac{\partial x}{\partial z} ~~~ \mbox{(d)} \]
10-1.式(c)が成り立つことを教員 Y にもわかる程度に説明せよ。
10-2.式(d)を\(z = 0\)で \(x = x_0\)、\(z = L\) で \(x = 0\) という境界条件の下で解いて、
10-2a.広義のエーテル拡散流束\(J_{\rm{B}}\)が次式で与えられることを示せ。
\[ J_{\rm{B}} = - \frac{D c}{L} \ln (1 - x_0) \]
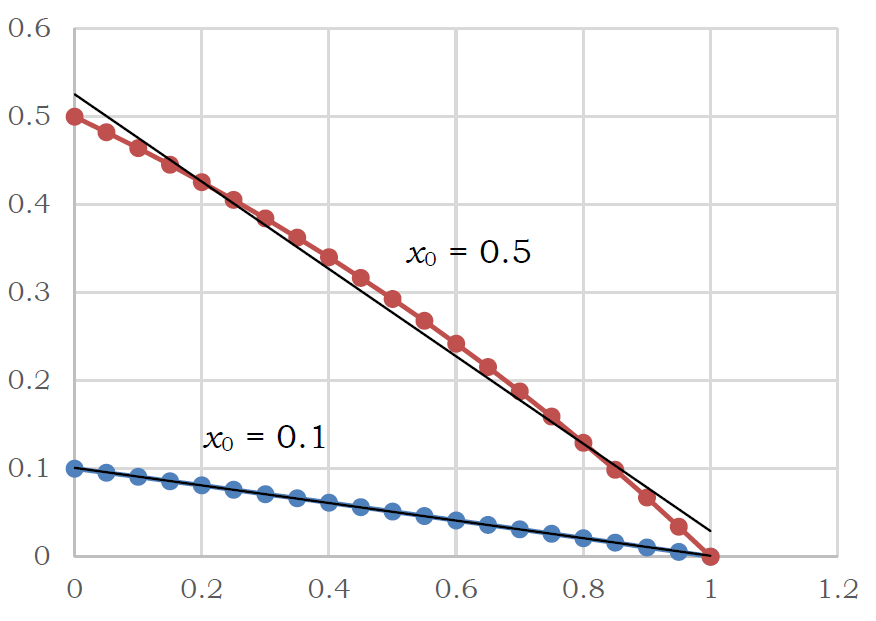
10-2b.管内のエーテルのモル分率 \(x\)、および狭義の拡散流速 \(j_{\rm{B}}\) が広義のエーテル拡散流束 \(J_{\rm{B}}\) に占める割合が、 \(z\) とともにどのように変化するかを、\(x_0 = 0.1\)、\(x_0 = 0.5\) の場合について図示せよ。
空気の流れはないので
JA = jA + cAu = 0
が成り立っているはず。また狭義の拡散流束については B が拡散するのと同じだけ A の拡散が生じることが期待される
jA = -jB
したがって
JA + JB = JB = (jA + jB) + (cA + cB)u = (cA + cB)u
より
u = JB/(cA + cB)
\[ J_{\rm{B}} = - Dc \frac{1}{1 - x} \frac{\partial x}{\partial z} = Dc \frac{\partial \ln(1- x)}{\partial z} \]
から
\[ \int_0^L J_{\rm{B}} \rmd z = J_{\rm{B}} L = Dc \ln \frac{1 - x(L)}{1 - x(0)} = -Dc \ln (1 - x_0) \]