
実を言えば、当化学教室の講義の中で、 粘度や熱伝導といった、 実験する上で非常に重要な話題はほとんど登場しません。 ここではたぶん小学校で習って以来、 学校の理科では触れられてこなかった、 粘さや熱伝導、拡散などに関わる話題を取り上げます。
1.【14年度試験問題から】U君は試験に次の問題が出ると聞いて自宅で試しに解いてみた。 U君と妹のPちゃんについての文章を読み、問いに答えよ。

(1) 流量を半分の0.5 L/minにしたら、AとBの出口の水温はそれぞれ何 °Cになるだろうか?
またさらに流量を減らし0.2 L/minにしたらどうだろう?
(2) B の流れの向きを逆転させ、Aと並行に水を流すようにしたとしよう。
流量が0.5 L/minの時、AとBの出口の水温はそれぞれ何 °Cになるだろうか?
また流量を 0.2 L/minにしたらどうか?
P:出口と入口で A が x °C 下がると、Bも同じだけ上がるわよね。 だから A と B が接触している間、A と B の間の温度差は一定で 90 - (10 + x) = 80 - x。 A の温度が下がる度合い x は、A と B の接触時間と、A と B の温度差に比例するにちがいないわ。 接触している長さを 1 として流れの速さを v とすれば、k を定数として
\[ x = \frac{k} {v} (80 - x) \]
つまり\[ x = \frac{80 k}{v + k} \]
になるわけよね、お兄ちゃん。 \(v\) が 1 で \(x\) が 20 だから \(k\) は1/3かしら?U:さすがはわが妹。ややこしい話を持ち出してきては、 結局アンチョコを写すしかない能のない Y やどこぞの理学部の小賢しい学生とは大違いだ。
A と B を並行に流す場合には、温度差は距離 \(y\) とともに変化する。 この場合温度差は イ で表され、 微小な距離 \(\rmd y\) を考えると接触時間は \(\rmd y/v\) だから、\(\rmd y\) 進んだ時の \(x\) の変化 \(\rmd x\) については次式が成立する:
\(\rmd x = (k \rmd y / v) \) イ つまり \(\rmd x / \rmd y = kv\) イ
だから出口におけるxの値は\(x = 40[1 - \exp(-2k/v)]\) (a)
P:お兄ちゃん。分子分母はdで約分できるよ・・・・・・1-1.P ちゃんの答えも参考に、流量が0.5 L/min、0.2 L/minの時のAとBの出口の水温を求めよ。
1-2. イ に当てはまる式を入れ、(a)式が得られることを示せ。 またAとBに並行に水を流した時、流量が0.5 L/min、0.2 L/minの時のAとBの出口の水温を求めよ。
2.厚さ2.0 mmのステンレスの板の上に厚さ1.5 mmのガラス板を密着して重ねて置いた。 ステンレス板の下面を200 °Cに、ガラス板の上面を100 °Cに保ったとすると、 定常状態でステンレスとガラスの接触面の温度は何°Cになるか? またステンレスの板とガラス板の間に厚さ 0.1 mmの紙を差し込んだとすると、 紙の上下面の温度差は何°Cになるか? ステンレス、ガラス、紙の熱伝導度をそれぞれ 16、1.2、0.06 W m-1 K-1 であるものとする。
3.室温が20 °Cで外気の気温が -10 °C の時、部屋の窓からの放熱を考える。 窓が厚さ 6 mm で熱伝導度 1.0 W m-1 K-1のガラスの板1枚で仕切られていて、 風がなく自然対流の影響で空気との間の熱伝達率が内外ともに 2 W m-2 K-1であるとする。
3-1.窓の面積を 1.0 m2として単位時間当たりの放熱量を評価せよ。
3-2.風が吹いてガラス窓の外側の熱伝達率が30 W m-2 K-1になったとする。 単位時間当たりの放熱量はいくらになるか。
3-3.ガラス窓の外に木製の雨戸(厚さ5 mm 熱伝導度 0.2 W m-1 K-1)を取り付けた。 この雨戸とガラス窓の間には風が吹き込まず、内側の空気との熱伝達率は雨戸もガラス窓も同じく 2 W m-2 K-1であり、 雨戸の外側の熱伝達率は30 W m-2 K-1であるとする。 窓からの単位時間当たりの放熱量はいくらになるだろうか? また雨戸とガラス窓の間の空気の温度は何 °Cになるだろうか?
4.プロパンC3H8の燃焼について次の問いに答えよ。
4-1.プロパンを燃焼させ完全に二酸化炭素と水にするには、 プロパンと空気の体積比をいくら以上にする必要があるか?空気中の酸素のモル分率を0.2とする。
4-2.プロパンと空気の混合ガスの密度 1.2 kg m-3、熱容量1.0 J g-1 K-1、 燃焼ガスの熱伝導度を0.024 W m-1 K-1とする。 混合ガスの点火温度を550 °C、生成する燃焼ガスの温度が1900 °C、燃焼領域の幅が 0.20 mmとして、 マラール・ルシャトリエの式を用いて20 °Cのプロパン-空気混合ガスの燃焼速度を計算せよ。
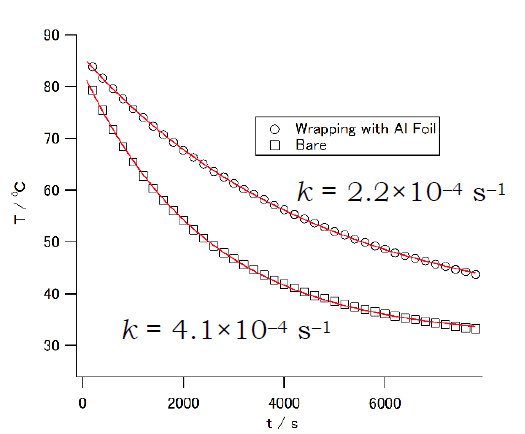
5.【15年度試験問題から】ナス型フラスコに湯を100 mL入れて、室内(室温は28 °Cでほぼ一定で無風状態)に放置した時の温度変化を、 裸で置いた時とアルミホイルで包(くる)んだ時とで比較した結果を図に示す。 この冷却挙動を考察した以下の文章を読み、問いに答えよ。
\[ \frac{\rmd T}{\rmd t} = -k (T - T_{\rm{e}}) \]
\(t\) = 0で \(T = T_0\)とすると温度変化は次式のように表される:\(T\) = \(T_{\rm{e}}\) + イ
実際にデータに当てはめてみると、当てはめは非常によく、 係数 \(k\) はアルミホイルで包むことで 4.1×10-4 s-1 から2.2×10-4 s-1 にほぼ半分になっている。5-1.文中の イと ニ には適切な数式、ロ、ハ、ホには適切な数値を記し、{ A }、{ B }については適切な語を選べ。
5-2.上ではナス型フラスコを綿布で一重に包んだが、二重にすると熱伝達率は裸のフラスコに比べてどれだけ小さくなるか。またアルミホイルを二重にするとどうか。
6.下記の無能の昭和老人Yの妄想には、どの点に問題があるだろうか?Y にも分かるように説明せよ。
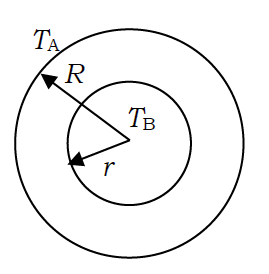
7.沸騰熱伝導において、極大熱流束(限界熱流束critical heat flux)を推算する式として次のZuberの式はよく知られている:
\[ q_{\rm{max}} = C_{\rm{KZ}} \Delta_{\rm{vap}}H \rho_{\rm{V}} \left[ \frac{\sigma g (\rho_{\rm{L}} - \rho_{\rm{V}})}{\rho_{\rm{V}}^2} \right]^{1/4} \]
ここで σ は表面張力、g は重力加速度、ΔvapH は蒸発のエンタルピー変化、 ρL、ρVはそれぞれ液体、蒸気の密度であり、 CKZ は定数でここでは0.15とする。Zuberの式を用いて次の問いに答えよ。
7-1.水の沸騰熱伝導における極大熱流束はいくらになるか推算せよ。 沸点における ΔvapH = 2.3 kJ/g、σ = 60 mN/m、 ρL = 960 kg m-3、ρV = 0.60 kg m-3とする。
7-2.円筒形の容器の底面(面積300 cm2)をバーナーで加熱して蒸気を発生させる時、 1秒当たり最大何 g の水蒸気を発生させることができるか推定せよ。
8.内径15 mmの試験管の中に、試験管の口から5 cmのところまで水を入れ、試験管立てに立てて20 °Cの乾燥した部屋の中に置いた。 放置して定常状態になった時、水の蒸発による試験管中の水面の低下速度はどれくらいになるだろうか? 空気と水蒸気の拡散係数を 3 × 10-5 m2 s-1、水蒸気圧2.3 kPaとする。
9.試薬瓶のガラスの摺り合わせから、瓶の中に入っているヘキサンの蒸気がどの程度漏れるかを評価した次の文章を読み、問いに答えよ。
\[ \frac{\Delta P}{h} = \eta \frac{\rmd^2 u}{\rmd x^2} ~~~~ \mbox{(a)} \]
x = ±d/2 で u = 0 となるように u を決めると次のようになる\[ u = k (x^2 - d^2/4) ~~~~ \mbox{(b)} \]
ここで \(k = \Delta P / (2 \eta h)\) とおいた。 すきまの間の流体の平均流速は u = - イ であり、摺り合わせの間を通過する単位時間当たりの流量 Q は次式で与えられる:\[ Q = - \frac{\pi d r^3}{6 \eta h} \Delta P ~~~~ \mbox{(c)} \]
9-1.式(a)が成り立つことを教員 Y にもわかる程度に説明せよ。
9-2.イに適切な式を入れ、式(c)が成り立つことを示せ。
9-3.摺りの半径 r = 10 mm、高さ h = 20 mmで、摺りの間隔 d = 0.05 mmであるとする。 また試薬瓶内のヘキサンの蒸気圧は 20 kPaで一定で、空気の粘度はヘキサンの濃度によらず20 μPa sとする。
9-3a.外部の圧力は100 kPaで一定で、試薬瓶内部の圧力が室温の上昇にともなって104 kPaになったとしよう(5 °C程度の温度上昇に相当)。 ヘキサンで飽和した空気が毎分何mL漏れ出てくることになるか?これは毎分何gのヘキサンが漏れ出ることに相当するか。 またもし摺り合わせのよい試薬瓶で、摺りの間隔 d = 0.01 mmであるとすると漏れ出るヘキサンの量はどうなるか?
9-3b.空気中でのヘキサンの拡散係数を8 mm2 s-1とする。 試薬瓶の内外の圧力差がない場合、摺りの間隔 d = 0.05 mm、0.01 mmそれぞれの場合について、 拡散によってヘキサンが外部に漏れだす量は毎分何 g 程度になるか。
10.一般に流体系での拡散には、対流が大きな役割を果たす。
\[ J_{\rm{B}} = j_{\rm{B}} + n_{\rm{B}} ~~~ \mbox{(a)} \]
狭義の拡散流速 \(j_{\rm{B}}\) はフィックの法則から次式で表され\[ j_{\rm{B}} = - D \frac{\partial c_{\rm{B}}}{\partial z} ~~~ \mbox{(b)} \]
対流による拡散流速\(n_{\rm{B}}\)は、巨視的な流速\(u\)にエーテル濃度\(c_{\rm{B}}\)をかけたもの\(u c_{\rm{B}}\)に等しい。 ここで問題は巨視的な流速 \(u\) であるが、定常的な拡散なので空気Aの流れは存在しないはずで、 巨視的な流速\(u\)は、広義のエーテル拡散流束 \(J_{\rm{B}}\) によって引き起こされる巨視的な流れの速度に等しく、次式が成り立つ:\[ u = \frac{1}{c_{\rm{A}} + c_{\rm{B}}} J_{\rm{B}} ~~~ \mbox{(c)} \]
管内の圧力 \(P\) ・温度 \(T\) は一定と考えられるので、空気とエーテルの濃度の和 \(c_{\rm{A}} + c_{\rm{B}} = P/RT = c\) は一定であり(\(R\) は気体定数)、 エーテルのモル分率を \(x (= c_{\rm{B}}/c) \) とすると広義のエーテル拡散流束 \(J_{\rm{B}}\)について次式が成り立つ\[ J_{\rm{B}} (1 - x) = - D c \frac{\partial x}{\partial z} ~~~ \mbox{(d)} \]
10-1.式(c)が成り立つことを教員 Y にもわかる程度に説明せよ。
10-2.式(d)を\(z = 0\)で \(x = x_0\)、\(z = L\) で \(x = 0\) という境界条件の下で解いて、
10-2a.広義のエーテル拡散流束\(J_{\rm{B}}\)が次式で与えられることを示せ。
\[ J_{\rm{B}} = - \frac{D c}{L} \ln (1 - x_0) \]
10-2b.管内のエーテルのモル分率 \(x\)、および狭義の拡散流速 \(j_{\rm{B}}\) が広義のエーテル拡散流束 \(J_{\rm{B}}\) に占める割合が、 \(z\) とともにどのように変化するかを、\(x_0 = 0.1\)、\(x_0 = 0.5\) の場合について図示せよ。
11.【16年度試験問題から】Y がエバポレーターでは減圧する代わりに新鮮な窒素ガスを吹き込むことで十分だという説を唱えている。 この説が学生に無視されているのを哀れに思った U 君は大先輩の Q 先生に尋ねてみた。以下の U 君と Q 先生の会話を読み問いに答えよ。
U: 化学実験では減圧蒸留で使うダイアフラムポンプを使っていたので、
2 kPaぐらいにはなってると思ってたんですが圧力は高めですね。
ということはY説はそんなに間違ってるわけではないんですか?
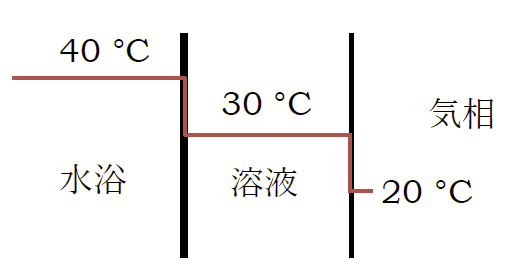
Q: まず熱伝導の立場から事態を見てみよう。
化学実験で使っているエバポレーターで、減圧しながら順調にフラスコ中のヘキサンを蒸発させている時の温度分布と熱の流れは、
定常状態では図のように整理できるだろう。
水浴の温度が40 °Cぐらいで、溶液の内部の温度はざっと30 °Cで溶液表面の温度は20 °C。
この表面から生じる蒸気を氷冷した冷却器で凝縮させるというかたちだ。
液体界面での熱伝達率はいろいろ変化するが、ここでは水浴-溶液、溶液-溶液表面の熱伝達率は同じで1000 W m-2 K-1 としよう。
フラスコと水浴の接触面積を 50 cm2 程度とすると、ヘキサンの蒸発熱はおよそ 300 J/g 程度だから イ 蒸発速度は0.2 g/s程度。
100 g 蒸発させるのに10分ぐらいというわけだ。
攪拌を激しくしたりしたら5分ぐらいにはなるだろう。
U: ちょっと乱暴な設定かと思いましたが、実際にやった体感と一致しますね。
この温度分布を実現するには、表面からかなりな速度でヘキサンが蒸発しないといけようですが、
Y説のように窒素を吹き込むのが有力に見えてきます。
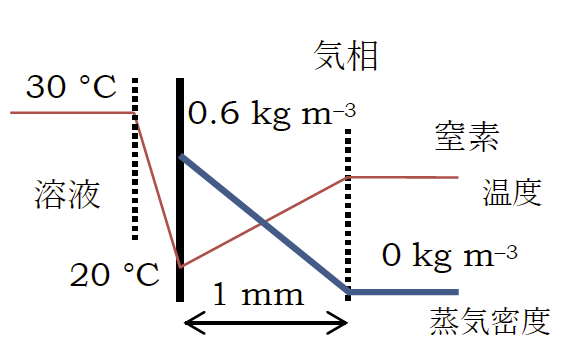
Q: 蒸発速度は溶液表面近傍のヘキサン蒸気の拡散速度に相当する。 ざっくり液面から 1 mm ぐらいの気相は(境界層で)動かず、その外は窒素という設定で考えることにしよう。 ヘキサンの 20 °Cの飽和密度は約 0.6 kg m-3 程度。 これが 1 mm ぐらいの層を通して窒素の中に拡散していく。 常圧で考えると、ヘキサン蒸気の拡散係数は 10 mm2 s-1 程度なので ロ 蒸発速度は 0.03 g/sでいささか足りない勘定になる。 水浴の温度を40 °C のまま、窒素吹込み法で濃縮するなら、ハ 溶液表面の温度は35 °C(ヘキサン蒸気の飽和密度1.0 kg m-3)くらいになり、 100 g 蒸発させるのに 30分ぐらいはかかるだろうね。
11-1.下線部イ、ロ、ハのようにQ先生が評価した根拠を、それぞれYにも分かる程度に説明せよ。
11-2.Q先生の議論を参考に、粘性の高い溶液をエバポレーターで濃縮するのに時間がかかる理由を述べよ。
12.【15年度試験問題から】液体中での沈降速度を利用して、炭酸カルシウム(カルサイト)粉末の粒径分布を調べる実験についての以下の文章を読み、問いに答えよ。
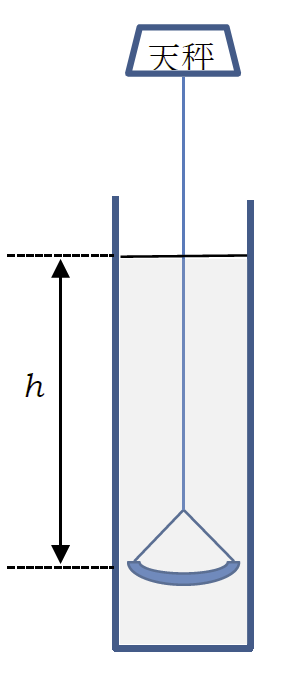
\[ v(a) = \frac{\Delta\rho g}{18 \eta} a^2 = k a^2 ~~~ \mbox{(a)} \]
ここで \(\Delta\rho\) は炭酸カルシウムと水の密度差、\(g\) は重力加速度、\(\eta\) は水の粘度であり、\(k = \Delta\rho g/18 \eta\) とした。 最初炭酸カルシウム粒子が均一に分散しているなら、炭酸カルシウムの沈降による天秤の示す重さ \(w(t)\) の増加速度は次式で与えられる:\[ \frac{\rmd w(t)}{\rmd t} = \frac{w_0}{h} \int_0^{a(t)} {v(a) f(a) \rmd a} ~~~ \mbox{(b)} \]
ここで \(w_0\) は最終的な増量 \(w(\infty)\)、\(f(a)\) は粒径 \(a\) の粒子の質量分布関数である。 また \(a(t)\) は時刻tで沈降が終了する粒子の直径で \(v(a(t)) t = h\) の関係から定まる。したがって\[ \frac{\rmd^2 w(t)}{\rmd t^2} = \frac{w_0}{h} \frac{\rmd a(t)}{\rmd t} v(a(t)) f(a(t)) ~~~ \mbox{(c)} \]
 天秤の示す重さの変化が図のように得られたとすると、時刻 \(t\) における接線の切片の値 \(b(t)\) の時間変化は次式で与えられる:
天秤の示す重さの変化が図のように得られたとすると、時刻 \(t\) における接線の切片の値 \(b(t)\) の時間変化は次式で与えられる:
\[ \frac{\rmd b(t)}{\rmd t} = -\frac{t}{w_0} \frac{\rmd^2 w(t)}{\rmd t^2} = \frac{\rmd a(t)}{\rmd t} f(a(t)) ~~~ \mbox{(d)} \]
したがって次式のように時刻 \(t_1\)、\(t_2\) における切片の値から、粒径 \(a(t_1)\) と \(a(t_2)\) の間の粒子の割合が評価できることになる:\[ b(t_2) - b(t_1) = -\int_{t_1}^{t_2} {\frac{\rmd a(t)}{\rmd t} f(a(t)) \rmd t} = \int_{a(t_2)}^{a(t_1)} {f(a) \rmd a} ~~~ \mbox{(e)} \]
12-1.(d)式が成立することを、無能の昭和老人 Y にもわかるように説明せよ。
12-2.沈降深さ \(h\) を30 cmとして実験を行い、図2の結果を得た。\(w(t)/w_0\) の切片の値 \(b(t)\) は、\(b(\rm{20 min) = 0.42}\)、\(b(\rm{40 min) = 0.69}\) であったという。 粒子の質量の累積分布 がちょうど 0.5 となる粒径 \(a_{50}\) はいくらか推定せよ。 またこの炭酸カルシウムがすべて粒径 \(a_{50}\) の粒子からなっているとすると、 1 gの炭酸カルシウムには何個の粒子が入っていることになるか? 炭酸カルシウムの密度を 2.7 g cm-3、水の密度を1.0 g cm-3、 水の粘度を1.0 mPa s、重力加速度を9.8 m s-2とする。
13.温度 \(T_{\rm{m}}\) に保った直径 \(d\) の細長い金属線を、温度 \(T_{\rm{a}}\) 、風速 \(v\) の気流中に置いた時、 熱輻射の効果を無視すると、金属線の単位表面積あたりの放熱量 \(q\) は次式で評価されるという(Kingの式)
\[ q = \frac{k}{d} (A + B \sqrt{vd/\nu} ) (T_{\rm{m}} - T_{\rm{a}})~~~~ \mbox{(X)} \]
ここで \(k\) と \(\nu\) はそれぞれ気体の熱伝導度と動粘度であり、\(A\)、\(B\) はともにおよそ0.5程度の定数である。
13-1.式(X)はレイノルズ数 \(vd/\nu\) が1~5000程度で成立するという。 金属線の直径が 50 μmであるとすると、空気中で風速が何m/s程度の範囲で成立することになるか。 空気の熱伝導度を0.026 W m-1 K-1、動粘度を16 mm2/sであるとする。
13-2.熱線式の風速計は式(X)に基づき、抵抗線に電流を流して発生する熱量と、抵抗線と気体の温度差をモニターすることで風速を測定する。 電気抵抗が1 mあたり40 Ω の直径50 µmの抵抗線を用い、抵抗線温度 \(T_{\rm{m}}\) を80 °Cで一定になるように抵抗線に流す電流値を制御したとしよう。 風速10 m/s、20 °Cの気流中に置いたとき、電流をどれぐらい流す必要があるか。 また風速1 m/sの時はどうか。かんたんのため \(A = B = 0.5\) とする。
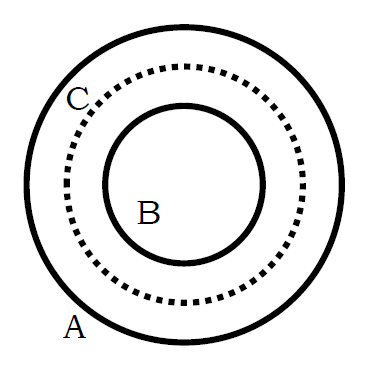
14.半径8 cmの長い円筒 A の中に半径 4 cm の円筒 B を入れ、それぞれの温度を 420 K と 380 K に保った。 AとBは黒体としてふるまうとして、次の問いに答えよ。
14-1.AからBに 1 m2あたり1 s 間に輻射熱で何Jの熱が移動するか。 ステファン-ボルツマン定数 σ = 5.7 × 10-8 W m-2 K-4 とする。
14-2.A と B の間に半径 6 cmの黒体の円筒 C を挿入したとする。定常状態において A から B に 1 m2あたり 1 s 間に輻射熱で何 J の熱が移動することになるか。
15.【14年度試験問題から】以下の文章を読み問いに答えよ。
\[ S_v = 14 \sqrt{\frac{\Delta P}{\eta u L} \frac{\epsilon^3}{(1 - \epsilon)^2}} \]
これが Kozeny-Carman の式とされているのだが、コピペの教師 Y がプリントに書いていた式と係数が違っている。 不審に思った N 君が大先輩の Q 先生に尋ねたところ、 Q 先生は「Y君は若いからね。ぼくらは記号の書体なんて気にしなかったし、CGS単位系で圧力差だけはmmH2O。 それにどうせ有効数字2ケタ程度の話だから」と仰った。 Q先生の話を手掛かりに、N君は次のように考えた:この公式中の \(S_v\) や \(L\) などは物理量ではなく数値なのだろう。 もしすべてがCGS単位系で統一されておれば、余分な係数は出てこないはずだ。 Q先生の話を信じれば圧力が mmH2O とのことだが、これは高さ 1 mm の水柱のおよぼす圧力だから、 CGS単位系に直せば、重力加速度 9.8 m s-2 で水の密度を 1.00 g cm-3 として、
1 mmH2O = イ dyn/cm2
だからCGS単位で表した圧力差 ΔPCGS dyn cm-2を使うと 、上の公式中の ΔP を次のように置き換えればよい
ΔP = ロ ΔPCGS
しかしこれではコピペの Y の書いていた式と合わない。 Q先生は ハ をmmH2O と思い違いしておられたのだろう。 そう考えればつじつまが合う。15-1.文中の イ~ハに当てはまる適切な数字・数式あるいは単位記号を記せ。
15-2.空隙率が 0.58 の炭酸カルシウムの粉末を断面積 0.80 cm2 のガラス管に高さ12 cmになるように詰め空気を流した。 水を入れたU字管で、粉末層にかかる気圧差を測定したところ 8.0 cmH2Oで、 空気は毎分24 cm3 の速度で流れた。 この炭酸カルシウムの粉末が直径 \(d\) の球形粒子からなるとすると \(d\) は何 µm だろう? また単位質量あたりの表面積を評価せよ。この温度での空気の粘度を0.019 mPa s、炭酸カルシウムの結晶の密度を2.7 g cm-3とする(1 P(ポアズ) = 0.1 Pa s、\(d = 6/S_v\)で評価されることに注意せよ)。
CGS系の圧力の単位としてbarye(バリ)、単位記号b(ba、Baとも。1 b = 1 dyn cm-2)があるが 、bar(= 0.1 MPa)と紛らわしくあまり(ほとんど)使用されない。
16.断面積 1 cm2のガラス管に、直径0.70 mmの球形粒子からなるイオン交換樹脂を10 cmの高さ分だけ詰めて、水を流下させる。 水はちょうどイオン交換樹脂が浸った状態にしているものとする。
16-1.外部から圧力を加えず、重力で水を流下させるとき、イオン交換樹脂カラムに働く圧力勾配 ΔP/L は何 Pa/m と評価されるか?
16-2.詰めたイオン交換樹脂は十分水を切った状態で 6.5 g、それに十分水を浸した状態で 10.5 gであったという。 空隙率 ε はいくらか?
16-3.水の粘度を1.0 mPa sとし、コゼニー-カルマンの式に基づいて、水がどの程度の速度で流下するか評価せよ。
16-4.イオン交換樹脂が水酸化物イオンとイオン交換して膨潤し直径が 0.72 mmになったとする。 イオン交換樹脂を詰めた高さが変化しないとすると、この状態で水を流した時の流速は前問に比してどうなるか。
17.濃度30 g/Lの食塩水の入ったサンプル管と真水の入ったサンプル管を、断面積が1 mm2 長さ10 cmのチューブでつないだ。 十分時間がたって定常状態に達した時、水の入ったサンプル管への拡散による食塩の流入速度は、 30 g/Lの食塩水が何m/sの流速で流入してくることに相当するか? 食塩の拡散係数を1.6×10-9 m2 s-1とする。
18.大きな黒体の板AとBを平行に対向させて置き、Aの温度を420 K、Bの温度を380 Kに保った。
18-1.AからBに1 m2あたり1 s間に輻射熱で何 J の熱が移動することになるか。 ステファン-ボルツマン定数σ を 6 × 10-8 W m-2 K-4とする。
18-2.AとBを420 Kと380 Kに保ったまま、黒体の板をもう1枚AとBの間に平行に挿入したとする。 この時、定常状態においてAからBに1 m2 あたり1 s間に輻射熱で何 J 移動することになるか。 また2枚入れた時にはどうか?
19.【19年度試験問題から】小学校でも学ぶように、水溶液を用いた実験のろ過操作の際、 ろ紙は4つ折りにしてロートに密着させるのが原則である。

Q: ろ紙をロートに密着させることで、ロートの足に水が溜まるようになり、ろ過が効率的に進むようになる。
U: 数cmの水柱でそんなに効率が変わるでしょうか?
Q: ダルシーの法則によると沈殿を通過する流速は、圧力勾配に比例する。 ろ紙上に沈殿層が 1 mm積もっているとしよう。 沈殿層中の水の自重だけなら、圧力勾配はおよそ イ kPa/m程度だ。 もしロートの足に5 cm分の水柱があったら、この水柱分の圧力が 1 mmの厚さの沈殿層に働くとして、 圧力勾配は ロ kPa/m増加する。
U: 密着させたといっても隙間はあるわけですから、そこから空気が漏れてきますよね?
Q: 密着させた時の隙間を \(a\) としよう。 表面張力を \(\gamma\) とし、ガラスや紙が水によく濡れるとすれば、表面張力による吸い上げの圧力は \(2 \gamma /a\) で評価できる。 水の表面張力は70 mN/m程度だから、\(a\) がコピー用紙の厚み 0.1 mmなら \(2 \gamma /a\)= ハ Paで、 ニ cm程度の水柱なら支えられる。 エタノールなど通常有機溶媒では表面張力が20~30 mN/m程度なので、せいぜい ホ cmぐらい。 4つ折りは止めてひだ折りろ紙を使うのがいい。
U: こうした表面張力が効くケースはいろいろありそうですね。
Q: 薄層クロマトグラフィー(TLC)で溶媒の吸い上げられる現象にも関わっているよ。
Y: (突然割り込んできて)TLCのプレートに付いているシリカゲルの粒子の隙間を \(a\) とし高さ \(h\) まで溶媒が吸い上げられた状態を考えると、 先ほどの圧力の推定を利用して、十分表面張力の効果が大きければ、ダルシーの法則から \(t\) を待ち時間、\(k\) を定数、\(\eta\) を溶媒の粘度として次式が成立する:
\[ \frac{\rmd h}{\rmd t} = \frac{k}{\eta} \frac{\gamma}{ah} \]
従って吸い上げられる高さhは待ち時間 \(t\) を2倍にすると ヘ 倍になる。U: 怪しい議論だけど、酢酸エチルは25 °Cで \(\gamma/\eta\) が 55 m/s、ヘキサンは 60 m/sでだいたい同じだ。 有機実験で酢酸エチルとヘキサンの混合溶媒を使ったけれど、混合比を変えても TLC にかかる時間があまり変わらなかったのは、これで説明がつきそうだ。
Q: TLCの溶媒の選定には溶媒の極性が注目されがちだけれど、 実際に実験する上では吸い上げの速度にも注意が必要だ。ト このことはTLCに塗布されているシリカゲルの粒径についても言える。
19-1. イ ~ ホ に適切な整数値を、ヘには適切な数あるいは数式を入れよ。
19-2.下線部トについて、シリカゲルの粒径を微細にしていくとどのような問題が生じるか、コゼニー-カルマンKozeny-Carmanの式を参考に述べよ。