問 14

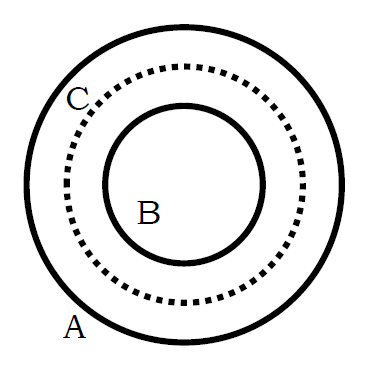
14．半径8 cmの長い円筒 A の中に半径 4 cm の円筒 B を入れ、それぞれの温度を 420 K と 380 K に保った。 AとBは黒体としてふるまうとして、次の問いに答えよ。

14-1．AからBに 1 m²あたり1 s 間に輻射熱で何Jの熱が移動するか。 ステファン-ボルツマン定数 σ = 5.7 × 10^-8 W m^-2 K^-4 とする。

14-2．A と B の間に半径 6 cmの黒体の円筒 C を挿入したとする。定常状態において A から B に 1 m²あたり 1 s 間に輻射熱で何 J の熱が移動することになるか。

14-1．

円筒の長さを L とする。 A → Bの熱の移動は 2π r_BL σ T_A⁴ であり、 B → Aの熱の移動は 2π r_BL σ T_B⁴。 Aの単位面積当たりの放熱量は

\[ \frac{2 \pi r_{\rm{B}} L}{2 \pi r_{\rm{A}} L} \sigma (T_{\rm{A}}^4 - T_{\rm{B}}^4) \approx \frac{r_{\rm{B}}}{r_{\rm{A}}} 4 \sigma \left(\frac{T_{\rm{A}} + T_{\rm{B}}}{2} \right)^3 (T_{\rm{A}} - T_{\rm{B}}) = 290 ~\rm{W~ m^{-2}} \]

14-2．

中間に黒体の円筒 C を入れた場合、円筒間の熱流束の釣り合いを考えると \(J = J_{\rm{A \to C}} - J_{\rm{C \to A}} = J_{\rm{C \to B}} - J_{\rm{B \to C}}\) より \(r_{\rm{C}}T{\rm{A}}^4 - r_{\rm{C}}T{\rm{C}}^4 = r_{\rm{B}}T{\rm{C}}^4 - r_{\rm{B}}T{\rm{B}}^4\) なので

\[ T_{\rm{C}}^4 = \frac{r_{\rm{C}} T_{\rm{A}}^4 + r_{\rm{B}} T_{\rm{B}}^4}{ r_{\rm{B}} + r_{\rm{C}}} \]

したがって A の単位面積当たりの放熱量は

\[ \frac{J}{2 \pi r_{\rm{A}} L} = \frac{r_{\rm{C}}}{r_{\rm{A}}} \sigma (T_{\rm{A}}^4 - T_{\rm{C}}^4) = \frac{r_{\rm{C}}}{r_{\rm{A}}} \sigma \left( T_{\rm{A}}^4 - \frac{r_{\rm{C}} T_{\rm{A}}^4 + r_{\rm{B}} T_{\rm{B}}^4}{ r_{\rm{B}} + r_{\rm{C}}} \right) = \frac{r_{\rm{C}}}{r_{\rm{A}}} \frac{r_{\rm{B}}}{r_{\rm{B}} + r_{\rm{C}}} \sigma (T_{\rm{A}}^4 - T_{\rm{B}}^4) \\ = \frac{r_{\rm{C}}}{r_{\rm{B}} + r_{\rm{C}}} \frac{r_{\rm{B}}}{r_{\rm{A}}} \sigma (T_{\rm{A}}^4 - T_{\rm{B}}^4) \\ = \rm{ \frac{6~ cm}{4~ cm~ +~ 6~cm} \times 290~ W~ m^{-2} = 175~ W~ m^{-2} } \]