解説：オルンシュタイン－ゼルニケ（Ornstein-Zernike）理論のアウトライン

オルンシュタインとゼルニケは、現象論的な立場から、 密度の揺らぎについての表式を与えた （L.S. Ornstein and F. Zernike, Proc. Akad. Sci. (Amsterdom), 17, 793 (1914)）。 彼らの議論の概略を、今回の話に資する範囲で紹介する。

●分子数の揺らぎと分布関数

流体中に、ある体積 V の領域を考え、そこに見いだす分子数 N の揺らぎと、 局所的な密度の揺らぎの関わりを考える。 そのため、この領域を体積 v の多数の微小なセルに分割する。 かりにセルの体積が極めて小さく、見いだす分子数がせいぜい 1 個であるとすれば、 i 番目のセルに見いだす分子数 N_i の分散は、N_i が 0 か 1 の値しか取らないことから、

　　(A1)

であることと、(ρv)² は ρv に比べて極めて小さいことから、 見出す分子数の分散は次のようになる。

　　(A2)

これらの微小な体積を合せた、体積 V 中での揺らぎを考えると、

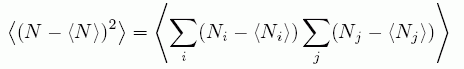　　(A3)

ここで、i = j の項と i ≠ j の項を分けると、

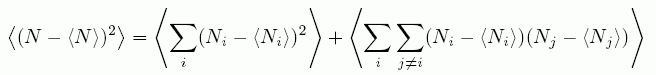　　(A4)

(A2)式を用いて、

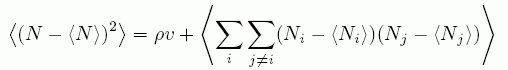　　(A5)

ここで、(A5)式右辺の第２項は、i についての和を書き直して、次のように書ける。

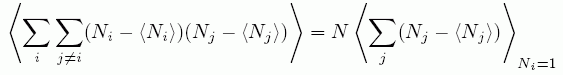　　(A6)

ここで < N_j - < N_j > > _{Ni = 1} は、 i 番目のセルに分子が１個ある時、j 番目のセルの分子数がいくら変化するかを示す。 したがって、(A5)式は動径分布関数を用いて、次のようになる。

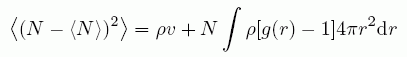　　(A7)

ρV = N だから、結局、次の式が成り立つ。

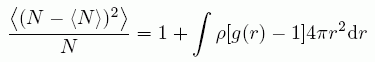　　(A8)

これと、(22)式の Q → 0 の極限を比べてみると、

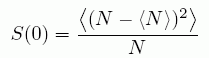　　(A9)

が成り立つことがわかる。

●密度分布に関わる積分方程式

次に空間的な密度揺らぎが、互いにどう関係し合っているかを考察する。 原点 O とそこから距離 r 離れた点 P の密度の揺らぎに注目する。 今、点 P 以外の密度を変化させないという条件の下、 O の密度を平均の密度ρから Δρだけ変化させたとしよう。 この時の点 P での密度変化 Δρ(r) を用いて、次の関数 c(r) を定義する。

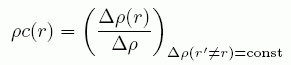　　(A10)

(A10)式では、２つの地点以外の場所での密度変化が起きないものと考えた。 しかし実際には、ある地点の密度の変化は、その近傍の密度変化を引き起こし、 そしてさらにそれが遠方の密度の変動を引き起こすといった現象が起きる。 そうした状況で、(A10)と同様に、次の関数 h(r) を考える。

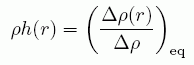　　(A11)

ここで、(A10)と(A11)式を用いて、Δρ(r) についての表現を整理すると、次の式が成り立つことがわかる。

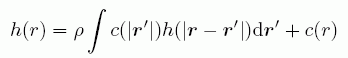　　(A12)

ここで、右辺第１項は、原点 O で起きた密度変化 Δρ によって距離 r' 離れた点 Q に誘起される密度変化が、 P 点に引き起こす密度変化を、すべての Q について足し込むことに相当する。 今日、この方程式を、オルンシュタイン－ゼルニケ（OZ）式と呼ぶ。

かりに h(r) が c(r) に比べて、距離についてゆっくり変動するとすれば、 十分遠いところでは c(r) は 0 と見なせ、かつ h(r-r') を r の周りで展開すると

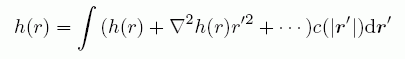　　(A13)

(A13)式を２次の項までに止めて整理すると、 h についての微分方程式として次の形の式が得られる。

　　(A14)

この方程式を解くと、大きな r での解として

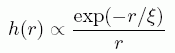　　(A15)

をえる。

ところで(A11)式の右辺は、ある微小領域に分子が存在する際に、 それから r 離れたところに見いだす分子数が、平均値からどれだけはずれているかを表わしている。 したがってそれは ρ[g(r) - 1] に等しく、次式が成り立つ。

　　(A16)

(A15)式と(A16)式から、(32)式が得られる。 (A15)式のフーリエ変換から、(33)式は得られる （歴史的には (33)式が先に発表され、(A15)式はその２年後 Zernike によって発表された）。

OZ 式を解くために、さまざまな近似理論が開発されてきた。 パーカス－イェビック（PY、Percus-Yevick）の近似では、 c(r) を、注目する２つの分子対について、２つの分子間に相互作用エネルギーが働く場合 （この時２つの分子間の動径分布関数は求める動径分布関数と一致する）と、 働かない場合（この時２つの分子間には、周りの分子との相互作用を通じた、 間接の相互作用しか働かない）の動径分布関数の差で評価する。 したがって、剛体球流体では、c(r) は分子コアの外では 0 になる。

●分子数の揺らぎと熱力学量の関わり

(A6)式の右辺の < ΣN_j - < N_j > > の意味を考えると、 これは１個の分子を系に持込んだ時に、何個の分子が系の外に放出されるかを示す量である。 １個の分子を持込んで、１個出ていけば簡単だ。 しかし、この場合それに加えて、１個の分子をその体積中に保持することによる圧力の変化、 つまり浸透圧に相当する圧力変化

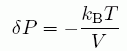　　(A17)

が生じる。ここで k_B はボルツマン定数、 T は絶対温度。 この圧力変化を補うために、外部から分子を導入する必要がある。 これだけの圧力変化を起こすには

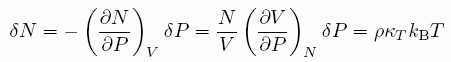　　(A18)

だけの分子数変化が必要になる。 ここで κ_T は等温圧縮率（-(1/V)(∂V/∂P)_T）。つまり (A5)式は次のように書ける。

　　(A19)

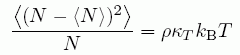　　(A20)

したがって、

　　(A21)

という関係が成り立つことになる。