∠XOY の内部に内接する円を描画する。 等比数列(R10)の系列の点を中心に内接円を描くと(上段)、 角度をうまく選べば、隣り合う円はすべて接する形にできる (この時、∠XOY = 13.21°)。
標準数というのは、 設計などで用いる数値の選定の基準となる数値です。 JIS のハンドブックでは、最後に数値の丸め方(JIS Z8401) とともに付録で掲載されています。
「数値の選定の基準」といっても、もう一つ分かりずらいかもしれませんが、 たとえば実験で使うビーカーのサイズをカタログで調べてみると、 ビーカーの容量/mL として 100, 200, 300, 500, 1000 といった数列がならんでいます。 日本ではこれが ”標準” ですが、 海外メーカーのカタログを見てみると、 100, 150, 250, 400, 600, 800, 1000 というのが ”標準” です(ISO 規格。ISO 3819)。 海外メーカーでは 500 mL のビーカーを揃えていないことが多いのです (「日本仕様」として揃えているメーカーもある)。 なぜこうなったか、 経緯はよく知りませんが、 JIS 規格(JIS R3503)の中には、「ビーカー」と「ビーカーR」の2通りの規格が併記され、 ビーカーR は ISO にならった規格になっています。 このように規格が併存し、みんながてんでに使用する状態になると、 取扱業者としては ..., 100, 150, 200, 250, 300, 400, 500, 600, 800, 1000, ... と細かく取りそろえる必要が出てきてしまいます。 こうした事態を避けるため(起きてしまったことはしょうがない・・・)、業種を問わず共通に利用できるガイドラインとして、 「標準数」というのが設定されているわけです。
| R5 | R10 | R20 |
|---|---|---|
| 1.00 | 1.00 | 1.00 |
| 1.12 | ||
| 1.25 | 1.25 | |
| 1.40 | ||
| 1.60 | 1.60 | 1.60 |
| 1.80 | ||
| 2.00 | 2.00 | |
| 2.24 | ||
| 2.50 | 2.50 | 2.50 |
| 2.80 | ||
| 3.15 | 3.15 | |
| 3.55 | ||
| 4.00 | 4.00 | 4.00 |
| 4.50 | ||
| 5.00 | 5.00 | |
| 5.60 | ||
| 6.30 | 6.30 | 6.30 |
| 7.10 | ||
| 8.00 | 8.00 | |
| 9.00 |
標準数として JIS で(ISO でも)採用されているのは、 101/5、101/10、101/20、 101/40(、101/80)の公比の等比数列の値を 「実用上便利な数値」に焼きなおしたものです(JIS Z8601)。 その昔 1878 年ごろ、ルナール Renard(飛行技術開拓者として有名)が発案したもので、 ルナール数列とも呼ばれ、それぞれの系列は ”R” を付け R5、R10、R20、R40(、R80) と呼ばれています ( ルナールはこの標準数を用いて、 425 種類あった係留気球 captive baloon のロープの種類を、 25 分の 1 の、17 種類にまで減らしたとのこと)。 左表には、R5、R10、R20 の系列を示しました。 なお JIS には規定がありませんが、 有効ケタを減らした R'、R'' 系列(たとえば 6.30 をざっくり 6.0 にしてしまう)と呼ばれるものもあります。
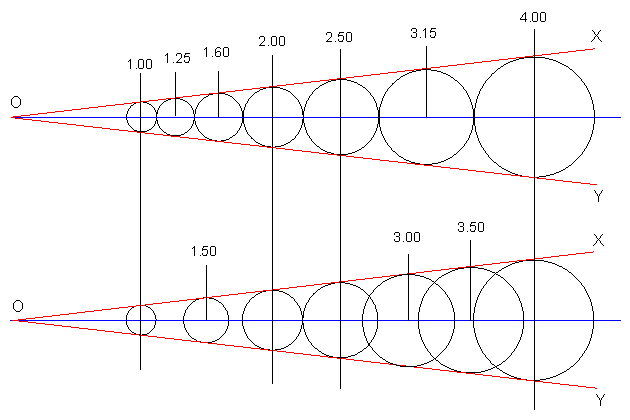
こうした数列は、音階の平均律で、 1オクターブを 21/12 の周波数比で分割しているのと似ていますが、 その狙い・考え方は随分違います。 等比数列を使用するのは、 扱う数値に一定割合の幅、不確かさを想定しているためです。 このことを表す印象的な図が、 米国 NBS(今日の NIST)の技術レポートに載っているので、 下に紹介しておきましょう。

∠XOY の内部に内接する円を描画する。 等比数列(R10)の系列の点を中心に内接円を描くと(上段)、 角度をうまく選べば、隣り合う円はすべて接する形にできる (この時、∠XOY = 13.21°)。
いずれも、1 から 4 の区間を 5 個の点で6 つの領域に区分し、 それぞれの点で ∠XOY に内接するように円を描いています。 等比数列(R10)であれば、∠XOY をうまく選べば、 図のように 7 個の円がちょうど接するようにできます (この時 sin(∠XOY /2) = (21/3 - 1)/(21/3 + 1) ≈ 0.115)、 ここで相似の関係から、それぞれの内接円の半径は等比数列(公比 = 22/3 ≈ 101/5) になっていて、R10 の系列をつかっておれば、 それそれの点の位置と内接円の半径の比(sin(∠XOY /2))は一定です。 つまり R10 の系列を使用すれば、 扱う数値に一定割合の幅を想定した時、 領域を均一にカバーすることができるわけです。
このように相対的な領域幅、不確かさを想定すると、 等比数列が望ましいわけですが、 そこにさらに 10 進法との相性、 実用上の使いやすさを加味して標準数は構成されています。 公比は 101/n の形ですし、 また数値も切りよく調製してあります。 正確に等比数列であれば、 標準数同士の乗除をおこなっても標準数になるはずですが、 R5系列で言えば、1.60 × 4.00 = 6.40 のはずですが、6.30 とみなすことになります。 多くの分野ではこれで問題ないでしょうが、 精密さを必要とする分野では大問題。 そこで別途、「計算値」(有効数字 5 ケタの数値)「理論値」も許容する形にJIS 規格は作られています。
このように工夫して構成された標準数ですが、 実際に標準数がどれほど一般的になっているかというと考えてしまいます。 最初に挙げたビーカーの容量もそうですが、 ネジやドリルの規格などにも、 標準数の影響はほとんど感じられません。 これは実際に使用するにあたって、 乗除以外に加減も重要な要素であることが影響しているのでしょう。 ぼくが出会った中では、 顕微鏡の倍率の規格(JIS B7254)で標準数が登場するのが、印象に残っていますが、 ここは対物・接眼レンズの倍率の乗算が重要な世界です。 標準数という考え方は重要ですが、 実際に標準数を適用するにあたっては、 どのような状況で、どのように利用されているかをよく見極める必要があるのでしょう。
この意味では、 抵抗やコンデンサーの標準数列(JIS C60063)は、 標準数と同様のアイデアに基づいていて、広く実用されているものになっています。 これは101/3、101/6、101/12、101/24、... の公比の等比数列の値を採用しています。 ここでは E3、E6、E12 の系列を紹介しておきます。 (102/3 = 4.641... ですが、 ”さじ加減” があって 47 になるなどしています)。
| E3 | E6 | E12 |
|---|---|---|
| 10 | 10 | 10 |
| 12 | ||
| 15 | 15 | |
| 18 | ||
| 22 | 22 | 22 |
| 27 | ||
| 33 | 33 | |
| 39 | ||
| 47 | 47 | 47 |
| 56 | ||
| 68 | 68 | |
| 82 |
抵抗やコンデンサーの電気回路では、 もっぱら比や積が重要になるので、 こうした等比数列に基づく標準数列が広く利用されるのは、 むべなるかなというところです。