
|
| 図 1. 単純化した化学天秤の釣り合いの構図 |
化学の実験において、たいていの場合、秤量はもっとも精度の高い測定で、 容易に 1 万分の 1、あるいはそれ以上の精度を得ることができます。 それだけに十分、秤量の原理・方法を理解しておくことが求められます。
一般に天秤には計量できる最大値(最大秤量)と、 読み取れる最小値(目量。感量)が設定されています。 「化学天秤」と呼ばれるものは、感量が 0.1 mg 以下程度の天秤で、 学生実験では最大秤量 100 g 程度のものを利用しています (お値段は現状 10 ~ 20 万円といったところ)。 精秤はこれでいいのですが、 合成実験やさほど精度を要しない用途には、最大秤量が 500 g、目量が 0.01 g ぐらいの電子天秤が、 現時点では一番適切だと思います (昔は十万円以上したこうした天秤が、 どんどん安く身近になり、今や小学生のお小遣い程度で入手できるようになったのは驚きです)。 なお最近は天秤に「最小秤量値」が記載されていますが、 これは 1/1000 の精度で秤量できる最小の重さに相当しています (感量の千倍程度。米国の薬局方 USP で表記が義務付けられている)。
今日ではもはや骨董品扱いを受けていますが、 化学天秤は 200 年以上にわたって研ぎ澄まされてきた機器で、 その機構・原理を知っておくことは有益でしょう。

|
| 図 1. 単純化した化学天秤の釣り合いの構図 |
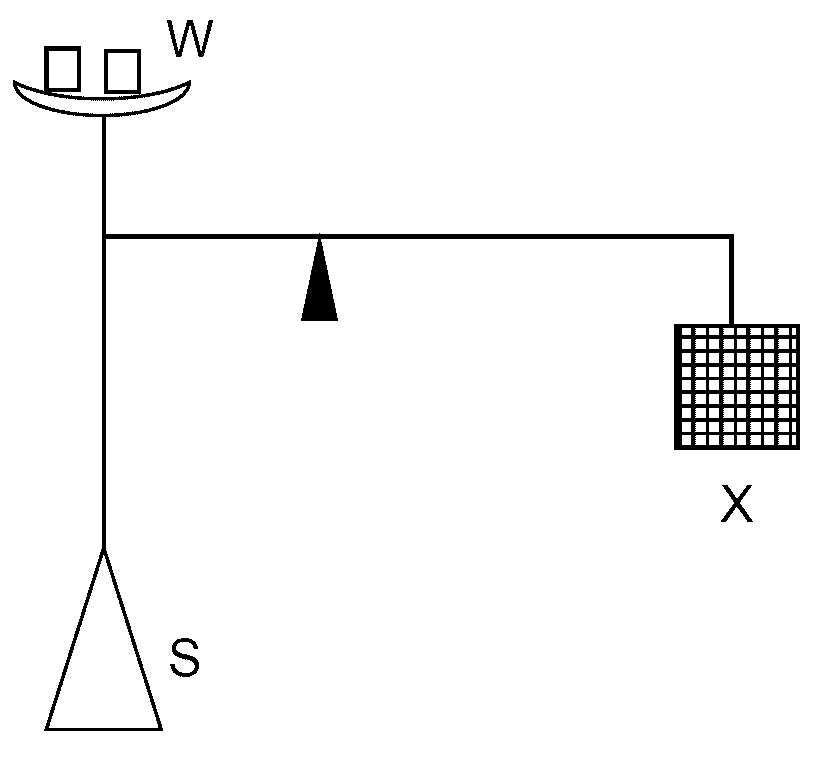
化学天秤は単純化すると、図1の弥次郎兵衛のような構造だといえます。 一方の端に質量 \(m + \Delta m\) の試料を、他方の端には質量 \(m\) の分銅をつり下げると、 水平から角 \(\theta\) ずれたところで釣り合います。 竿の重心が支点より下にあり、 試料と分銅の重さのちがい(\(\Delta m\))に応じて、竿の重心が移動するわけです。
支点から \(h\) だけ下に竿の重心があり、竿の質量を \(M\) とすると、 釣り合いの条件は次式で与えられます。
\begin{equation} (m+\Delta m) gL \cos \theta = mgL \cos \theta + Mgh \sin \theta \label{eq:balance} \end{equation}
振れる角度 \(\theta\) が小さければ \(\tan \theta \approx \theta\) なので、 天秤の感度 \(\alpha\) として次式が得られます。
\begin{equation} \alpha = \frac{\theta}{\Delta m} = \frac{L}{Mh} \label{eq:balsens} \end{equation}
装置の安定を保つ上で \(h\) はあまり小さくできないので、 天秤の感度を高めるには、竿を軽く(\(M\) を小さく)長く(\(L\) を大きく)することになります。 一方、感度を高めると、 竿の振れの周期が長くなって、安定するのに時間がかかるようになります。 また空気の対流など外部からの擾乱の影響も受けやすくなります。 必要とされる感度(概ね 0.1 mgで 0.01 rad 程度)と振れの周期を見越して天秤は設計されています。
|
| 図 2. 直示天秤の概念図 |
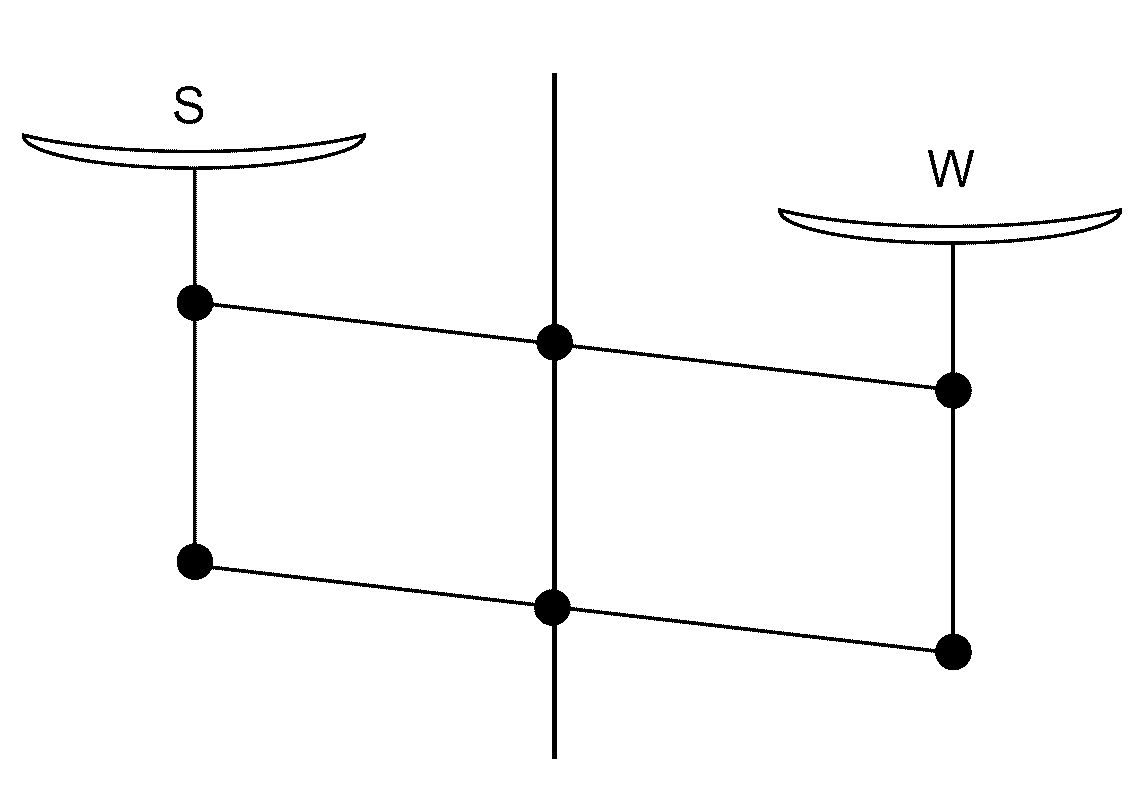
もし \eqref{eq:balsens} 式で与えられるように、天秤の感度が一定と見なせるならば、 竿の振れる角度を読み取ることで、 質量を詳細(典型的には 0.1 mg)まで決定することができるはずです。 けれども試料や分銅の重量で天秤にたわみが生じ、感度は荷重によって変化してしまいます。 直視天秤は、天秤にかかる荷重を一定に保ち、 触れ角を精密に読み取るようにした天秤で、 1980 年代ごろまで賞用されていました。
典型的な直示天秤は、竿や支点にかかる荷重を一定にし、 竿の振れる角度から質量の詳細 \(\Delta m\)を読み取るもので、 原理的には図2のような構造をしています。 X はあらかじめ決められた錘(おもり)で、測定する試料 S と分銅 W の質量の合計が、 Xと釣り合うことになります。 測定試料が重ければ分銅 W を減らし、軽ければ増やすことで、 竿や支点にかかる荷重を一定に保ち、感度が一定になるようにしてあります (この意味で「定感量天秤」と呼ばれることもあります)。 直示天秤では、測定される質量の値に天秤の感度が直接関係するので、 感度の調節は重要です。 釣り合いの位置を調節する水平方向の錘(調子玉)の調整に比して、 感度を調節するための垂直方向の錘(重心玉)の位置の調整は、 化学天秤以上に慎重に行う必要があります。
|
| 図 3. ロベルバル機構。 竿が傾いても重心は移動せず、復元力が働かない。 |
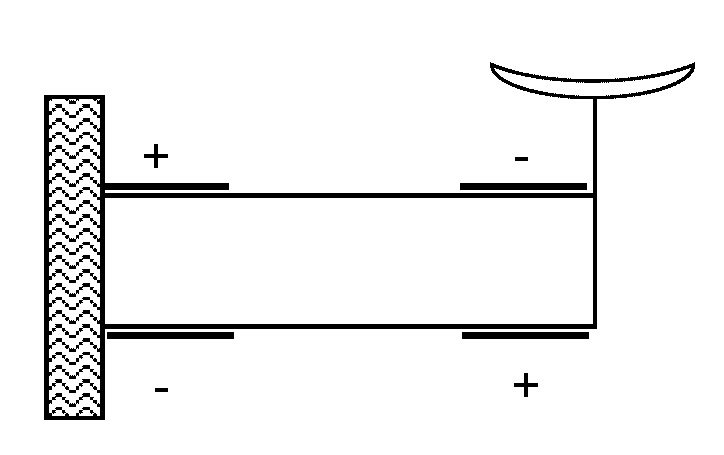
支点1つでやじろべえのように荷重を釣り合わせる形式では、図 1 のような下皿天秤にならざるを得ません。 上皿天秤は操作性の点からすぐれていますが、 上皿天秤を実現するには、図 3 のようなロベルバル Roberval 機構を取り入れる必要があります。 しかし可動点が必要で、下皿天秤に比して感度が落ちることは避けられません。
電子天秤は、元来は天秤における荷重の釣り合いの検出を目視に頼らず、 電気的な装置によって行い、荷重につり合わせるのに必要な力を電磁的に発生・評価するものです。 電子天秤は荷重の釣り合いを電磁的に検出することで感度を向上させ、 0.1 mg の感量を必要とする天秤(= 化学天秤)を上皿にすることを可能にしました。 典型的には電磁石を用い、そこに流れる電流値 \(i\) と荷重 \(mg\)(\(g\)は重力加速度)の線形の関係から秤量を行います。
\begin{equation} i = kmg + i_0 \label{eq:ebal} \end{equation}
この比例係数 \(k\) は装置の置かれた環境、特に気温に依存して変化します。 学生実験で用いる精密電子天秤は、較正用の精密分銅を内蔵しており、 較正キー操作をすると係数 \(k\) を評価しなおす仕組みになっています (気温の変化等を検知して、自動的に較正する機能を持った機種等もあります)。 なおこの較正によって、地域による重力加速度のちがい(高緯度ほど大きい)も補正されることになります。
|
| 図 4. 荷重をかけた時のひずみ |
今日電子天秤と言われるものの中には、荷重の釣り合いを利用する本来の意味での「天秤」でないものもあります。 ロードセル load cell を利用したものがその典型で、 荷重による支持物のたわみを評価することで荷重を測定する、いわばバネ秤です。 可動部が少なく堅牢で、食肉や野菜から、自動車・重機等の計量にいたるまで、 幅広く利用されています。 一般に金属材料はヤング率が 100 GPa 程度で、 10-6 程度のひずみを生じさせるには100 kPa(≈ 1 atm)程度の応力、 1 mm2 あたり 10 g 程度の荷重が必要となります。 このためロードセル型の電子秤の感度はあまり高くありません。 しかし材料・機構上の改良が進み、秤量値が 100 g、感量が 1 mg 程度のものも安く市販されるようになり、 学生実験でも利用します(最近は感量 0.1 mg のものも市販されています)。
0.1 mg程度までの精密な秤量の際の誤差の原因としては、 空気の熱対流と静電気が重要です。 まだ温かい試料を秤量皿に乗せて重さをはかると、 対流が起き、試料は軽く秤量されます(典型的には数 mg)。 むやみに秤量室に手を入れたり、体を天秤に近づけないようにします。 また、湿度が40%を下回る状態では静電気の影響が大きくなります。 プラスチックのビーカーは静電気がたまりやすいので、 精密な秤量に使用することは避けた方がよいでしょう。 また静電気が誘起されるので、試料容器をむやみに擦ったりしてはいけません。
なお、精秤の際に素手で時計皿等に触れるのは、 避けた方が無難ですが、 手が濡れたりしていない限り、 0.1 mg 程度の精度では影響が小さく、 あまり神経質になる必要はありません。 ただしあまり長く触って、 器具が温まると影響が出ます (手の油が付くはずなのに、かえって軽めの値が出る)。
たいていの場合、秤量は空気中で行われ、多かれ少なかれ空気の浮力の影響を受けています。 大気圧で液体が蒸発すると、体積がおよそ千倍程度になることを考えると、 1/1000 以上の精度の秤量には、空気の浮力の影響が無視できません。
試料を s、分銅が f、空気を a、の添字で表せば、 試料と分銅がつり合った状態では、次式が成り立ちます。
\begin{equation} M_\mrm{s} \left[ 1 - \frac{\rho_\mrm{a}}{\rho_\mrm{s}} \right] = M_\mrm{f} \left[ 1 - \frac{\rho_\mrm{a}}{\rho_\mrm{f}} \right] \label{eq:vouy} \end{equation}
電子天秤では、このつり合った状態での分銅の質量 \(M_\mrm{f}\) を、 試料の質量として表示しています。 したがって試料の質量 \(M_\mrm{s}\) は、表示される質量の値 \(M_\mrm{f}\) から、 次式で、与えられることになります(\(\rho_\mrm{s}, \rho_\mrm{f} \gg \rho_\mrm{a}\) としています)。
\begin{equation} M_\mrm{s} = \frac{1 - \rho_\mrm{a}/\rho_\mrm{f}}{1 - \rho_\mrm{a}/\rho_\mrm{s}} M_\mrm{f} \approx \left[ 1 + \left(\frac{1}{\rho_\mrm{s}} - \frac{1}{\rho_\mrm{f}} \right) \rho_\mrm{a} \right] M_\mrm{f} \label{eq:vouycorr} \end{equation}
空気の密度 \(\rho_\mrm{a}\) は通常の条件では 1.2 mg cm-3で、 \(\rho_\mrm{s}\) 、\(\rho_\mrm{f}\) は1~ 10 g cm-3 ですから、 0.1 %以上の精度にはこの補正が必要です。
通常の電子天秤では、\(\rho_\mrm{f}\) = 8.0 g cm-3 として浮力補正をして精確な質量になるように調整されています (電子天秤はさまざまな素材からできていますが、 実効的な分銅密度が 8.0 g cm-3 とみなせるということ)。 試料の密度がほぼ 1.0 g cm-3であれば、 秤量値を 1.00105 倍すれば真空中での秤量値となります。
かつては \(\rho_\mrm{f}\) = 8.4 g cm-3 の分銅(黄銅製)あるいは \(\rho_\mrm{f}\) = 7.9 g cm-3 の分銅(ステンレス製)の場合などについての浮力補正の表がハンドブック類に掲載されていたものでした。 分銅の密度 8.0 g cm-3 として浮力補正を行うのは OIML(国際法定計量機関)で定められた 「空気中の計量結果の協定値」に従っています。 JIS B7609「分銅」参照。