
|

|

|
| ビュレットに鉢巻きして読む。 この状態では見下ろす格好になっているので、 少ししゃがんで水平な位置に視線を持っていく。 | 老眼鏡が便利かも。 ルーペを使うのもあり。 ここでは合わせ技? | シェルバッハ(Schellbach)の青線。 青線が一番くびれて見えるところを読む。 好きな人は好きなようですが、個人的には好みでないです。 |
「最小目盛りの10分の1まで読む」ことが当たり前のように行われているが、 その根拠は必ずしも明らかではない。 なぜ 1/8 あるいは 1/12 ではなく 1/10 なのか。 また目視で全体の 1/2 の位置を判定するのと 1/3 の位置を判定するのでは、 難度が異なるはずである。 こうした問題を、web上の簡易なクイズを用いて検討する。
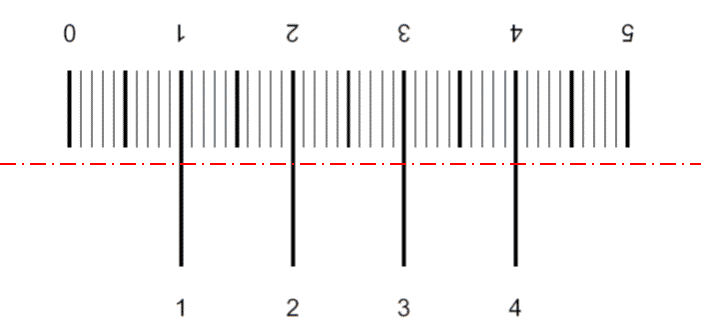
乱数で発生させた0.0~2.9の数字(「的」)が表示されるので、表示された「的」の値の位置にマウスポインターをセットしてクリックする。 Web上のフォームに、実際にクリックされた位置が0.01の桁まで表示される。おおむね30回以上行い、どの程度精確に位置を判定できるか調べる。
「的」の値を x、マウスでクリックした位置の値を y とし、y と x の差を δ(x) = y - xとする。 δ(x)はxが目盛り線上にある時(x = 0, 1, 2, 3)に 0 であり、 目盛り線に区切られた区間(0 ≤ x < 1, 1 ≤ x < 2, 2 ≤ x < 3)では同じ挙動を示すことが期待できる。 したがって以下では x の小数部分に注目し、δ(x)をxの値域を [0,1) とするランダム変数と考える。 また人間の目視が左右対称に行われるなら δ(x) と δ(1 - x) は同じ確率分布に従うと考えられる。
テキストのpdf版はこちら。
このクイズ、実際やってみてもらえたでしょうか? やった結果を整理するのに excel のシートを用意しています。 ちょっと動作が重いかもしれませんが、たいして考えずにカット & ペーストするだけで結果が出てくるはずです (もっと使い勝手の良いシートを作成していただける方を募集しています。よろしくお願いします!)。 ぼくがやってみた結果を下記に示します(用意した excel のサンプルにあるものです)。
| 偏差0.05超の頻度 | ||||
| 小数部 | 出現頻度 | + | - | 偏差平均 |
| 0.0 | 4 | 0 | 0 | 0.00 |
| 0.1 | 4 | 1 | 0 | 0.04 |
| 0.2 | 3 | 2 | 0 | 0.04 |
| 0.3 | 1 | 1 | 0 | 0.08 |
| 0.4 | 1 | 0 | 0 | 0.04 |
| 0.5 | 4 | 0 | 0 | 0.00 |
| 0.6 | 1 | 0 | 0 | -0.04 |
| 0.7 | 5 | 0 | 0 | -0.01 |
| 0.8 | 5 | 0 | 1 | -0.04 |
| 0.9 | 7 | 0 | 1 | -0.04 |
ちょっと偏差が大きいですが、小数部が 0.5 以下の時には偏差 (設定すべき位置より大きい時は +、小さいときは -)が + に、 0.5 以上では - に振れる傾向が見て取れます。 これは以前、この課題を始めた時に学生諸君の出した結果でも見られた挙動です。 2本の線の間の間隔を目視で何等分かにしようという時、 中央部の間隔は狭くなりがち。 そしてフツウの人ならだいたい 1/10 ぐらいが限界ということになるのでしょう。
なおこのテストを、試しに近くにいた学生さんにやってもらったところ、偏差のスコアはこの 1/3 ぐらい。 かろうじて偏差の正負の分布の判断ができる程度の結果でした。 人によって(年齢によって?)、こうした判別能力はずいぶん違うものなのでしょうね。
最小目盛の1/10までだいたい読み取れるとして、そこに若干の偏り(バイアス)があることは注意すべき点です。 化学実験で言えば、ビュレットのメニスカスの位置を読むというのが一番手近な例になるでしょう。 まずは正しく目盛りを見なければいけません(今回のweb クイズで言えばモニターの正面から見るというところでしょう)。 ビュレットのメニスカスについては読む位置・姿勢が重要で、 ビュレットを垂直に立て、水平方向から読みます (都合がよい値になるように、上からのぞき込んだり、下から見上げたりしない!)。 水平方向から眺めるのに、ロートをあてがう(ビュレットにロートを当て、足の方から潜望鏡のように目盛りを読む)、 ビュレットに紙テープで鉢巻きするなどは、 昔から伝えられる小技です。 またルーペを使って拡大するのは、読み取るストレスの解消になり(特に老人には必須)、 ぼくは百円ショップで売っている老眼鏡を使うことを推奨しています。 あるいはメニスカスの位置を際立たせる青線付きのビュレット(シェルバッハの青線)なども、 古くからある工夫です。

|

|

|
| ビュレットに鉢巻きして読む。 この状態では見下ろす格好になっているので、 少ししゃがんで水平な位置に視線を持っていく。 | 老眼鏡が便利かも。 ルーペを使うのもあり。 ここでは合わせ技? | シェルバッハ(Schellbach)の青線。 青線が一番くびれて見えるところを読む。 好きな人は好きなようですが、個人的には好みでないです。 |
滴定の開始点として、メニスカスの位置をたとえば2.00 mL など目盛りの切りのいいところに持ってくるのは感心しません。 たしかに開始点の読み取り誤差は小さくなります。 しかし終点の位置の小数部は、ランダムに出現するでしょうから、 たとえば 11.73 mL と読み取ったとしましょう。 こうなると滴定値として得た 9.73 mL について、単純に ± で誤差が語れなくなる、 読み取り誤差を考慮すると、若干プラスよりはマイナスの方に誤差範囲が広いはずです。 単発の実験ならさして問題なりませんが、多数のサンプルを分析する場合など、 こうした偏りが表に出てくることはあり得ます。 ですから、誤差は大きくなりますが(√2 倍)、 偏りが生まれ後の誤差評価を困難にするので、 開始点の位置はランダムに設定するのが望ましいのです。 同様に物差し(直尺)で、例えばカードの寸法を測る時、 物差しの 0 目盛りのところにカードの一端を合わせて測るのは好ましくないわけです。
この実験から分かるように、目盛りの中央の点については、 読み取り誤差は非常に小さくなります。 この発想を拡張していくと、10進法ではなく2進法で目盛りを刻んでいくというスタイルにたどり着きます。 これは長さにインチ inch を採用している米国などでよくあるやり方です。 日本ではあまりお目にかかりませんが、 たとえば自転車のチューブのサイズで 27 × 1 3/8 といった表記がしてあったりします。 これはチューブの外径 27 inch 幅が 1 3/8 inch ということで、 1/2、1/4、1/8、1/16 と言った具合に、 inch 以下を2進法で分割していく流儀を取っていることに由来しています。 読み取り誤差という点からは合理的と言えるでしょうが、 後の計算が厄介でぼくは敬遠です(特にインチのノギスのバーニアは避けたい)。

|

|
| mm の直尺。 0.5 mm の目盛線のついた目盛も用意されてはいる | 実験室にあった inch の直尺。 上方の目盛は十進法で刻んでいるが、 下方の目盛は二進法で刻んである。 |

読み取り誤差の課題は、90年にぼくが分析実験の改定に関わった時に導入したものです。 それ以降、最初に2人組で行う課題として実施してきました。 実験ペアの最初の共同作業というわけです。
 |
 |
| 物差し | 乱数表 |
この実験では乱数表を使ってもらいます。 今では乱数はexcel などでもお手軽に発生させることができますが、 そもそもの乱数の考え方とも関わって、乱数表の使い方になじんでおいた方がよいでしょう。 よく乱数表があればもうそれで乱数が得られると即断する人がいますが、 どのようにそこから乱数を取り出すかも重要なポイントなのです。
この課題で用意してある乱数表では、2桁の数の並びを200行20列、4000組与えています。 こうした乱数表から乱数列を得る際、常に左上から順次読み取っていくとすると、 実験を繰り返した際、乱数表の最初に位置する数値列の出現頻度を過大に評価することになります。 こうした問題を避けるため、表から0.0から4.9までの乱数列を効率的に抽出する手法として、 典型的には次のような手続きを取ります:
最初の読み取り位置は記録しておいた方がよいでしょう。 というのは、改めて同じ乱数列を使って「再現性」をチェックしたい場合もあるからです。 プログラミング言語の組み込みの乱数では、たいてい乱数の初期化の手続きの形で用意してあります (web のクイズで利用している Javascript の標準の乱数では「再現性のある」乱数はサポートされていません)。
今年度からweb 上のクイズに移行するについては、 化学実験の導入部をもう少し整理できたらという思いがありました。 従来のスケジュールでは初日のガイダンスの後2日かけて、 全体を15人程度ずつ4組に分け、「読み取り誤差」「ピペットの誤差」「ガラス細工」「実験室の使い方」の4課題をそれぞれ2時間程度で実施する形でした。 このような構成にしたのは機器の数が足りない(特に「ピペットの誤差」で使う化学天秤)こともありますが、 最初に小グループで学生相互、また多数の教員と触れる機会を持つのがよいだろうと考えていたからです。 でもこのところ、同時に同じ部屋でいろんな課題が走っていて、お互い顔も知らない同士、いろいろ話をする余裕もないままに、 雑然と過ぎてしまう傾向が強くなっているように思われました。 そこで実施課題を整理して「実験室の使い方」と「ガラス細工」を1日で実施、 「ピペットの誤差」は実験の基礎に入れ込み、「読み取り誤差」はweb 上の演習に切り替えるということにしたのです。
なお web 上のクイズといっても、ぼくがにわか勉強で Javascript で急遽仕立てたもの。 最近サポートされたという Javascript の Canvas を使っているので、 環境によってはうまく動作しない可能性があります(Win 10 の Chrome と FireFox、Android のスマホでは動作確認)。 最初の10回ぐらいはすぐに結果が見えるようにして感覚をつかんでもらい、 それ以降はすぐには結果が見えないようにして作業続行。 気が済むまでやったら、結果をカット & ペーストで用意してある excel シートに貼りつけ、解析という形です。 カーソルの形状などもいろいろ考えたのですが、 結局、標準カーソルを使う形に落ち着きました。 興味のある方もしおられれば、どうかもっと使い勝手の良いものを作っていただけるようにお願いします。
実際に学生さんたちにやっていただいた結果を取りまとめたレポートを作成しました。 レポートはこちらを見てください。 どうもカーソルの設定に難があるようで、 結果に偏りが見られています。 このあたりも含め、改定が必要なようで、新版のクイズを作ってみました (カーソルを十字型にして、十字を横軸に合わせる)。 どうでしょうね?
付記:21年度の学生さんに新版のクイズに取り組んでもらった結果をとりまとめています:
21年度読み取り誤差レポート
カーソルの形状を変えることで、
ほぼ 0.5 を中心に対称な結果が得られました。
こうしたことは、そもそものコンピューターの GUI の設計の中でもう研究済みなんでしょうが、
わずかなことでも影響するんですね。
(2021.7)