＜概要＞

温度 T_e の環境の中におかれた物体の温度T_Xは、熱伝導によって時間がたつにつれT_eになる。 この時の温度の時間変化は、多くの場合、物体と環境との温度差T_X - T_e に比例するとみなすことができる（ニュートンの冷却の法則）：

\begin{equation} \frac{\rmd T_{\rm{X}}}{\rmd t} = -k(T_{\rm{X}} - T_{\rm{e}}) \label{eq:newton} \end{equation}

比例係数 k を放熱定数、1/k を放熱の緩和時間と呼ぶ。積分形では式 \eqref{eq:newton} は次式のように表すことができる：

\begin{equation} T_{\rm{X}} - T_{\rm{e}} = (T^\circ_{\rm{X}} - T_{\rm{e}}) \exp(-kt) \label{eq:newtonint} \end{equation}

あるいは対数を取って

\begin{equation} \ln |T_{\rm{X}} - T_{\rm{e}}| = -kt + C \label{eq:newtonln} \end{equation}

ここで T°_Xは時間0における物体の温度を示し、C = ln |T°_X - T_e|である。 環境との温度差は時間 0.693/k（= (ln 2）/k）たつと半分になる（半減期）。 また温度 T_e⁽¹⁾ と T_e⁽²⁾ の２つ環境に接している場合には、 物体が定常状態で到達する温度T_X^∞は

\begin{equation} \frac{\rmd T_{\rm{X}}}{\rmd t} = -k^{(1)} (T^{\infty}_{\rm{X}} - T^{(1)}_{\rm{e}}) - k^{(2)} (T^{\infty}_{\rm{X}} - T^{(2)}_{\rm{e}}) = 0 \label{eq:newton2} \end{equation}

より次式で評価できる：

\begin{equation} T^{\infty}_{\rm{X}} = \frac{k^{(1)} T^{(1)}_{\rm{e}}) + k^{(2)} T^{(2)}_{\rm{e}}}{k^{(1)} + k^{(2)}} \label{eq:newton2x} \end{equation}

実験に先立ってＰＣにKeysight Handheld Meter Loggerをインストールしておくこと^*1。

^*1 Keysight のサイト https://www.keysight.com/ からダウンロードできる。 なお提供されているのは Windows 版のみである。

＜実験＞

1. ＰＣとマルチメーターU1251Aをケーブルで接続し、データ記録用のソフトKeysight Handheld Meter Loggerを起動する。 データ取り込み間隔は15秒程度でよい。（参考資料II-7参照）
2. ホットプレートスターラーの天板温度を90 °Cにセットして加熱し、 天板温度を90 °Cにする（通常１分程度で90 °Cに達する）。 放射温度計で天板温度を確認せよ（測る時は水を垂らすかテープを貼るかしないと、温度がかなり低めに出てしまうので注意）。
3. ビーカーに水を入れ、ポリエチレンラップで覆って水の蒸発を防ぎ、 ホットプレートスターラーの天板の上に置きスターラーで攪拌をおこなう。また水温の時間変化の記録を開始する。
4. 水温があまり変動しなくなったら記録を止める。
5. 新たに水を入れたビーカーを（３）と同様にホットプレートスターラーの天板の上に置く。 この時、スポイトで水を数mL垂らし、ビーカーと天板の間に水が入った状態にする。
6. スターラーで攪拌を始める。同時に水温の記録を開始する。
7. 水温があまり変動しなくなったら記録を止める。
8. 温度変化の様子をプロットし、天板とビーカーの間に水が満たされた場合とそうでない場合で、 最終到達温度と緩和時間を求め比較せよ。
9. 天板とビーカーの間に水を満たさない状態で、 ビーカーの水を80 °Cにするには天板の温度を何°Cに設定する必要があるかを予想し、実際に確認せよ。

＜検討＞

1. ポリエチレンラップで覆わない場合はどうなるか試してみよ。

＜実験例＞

ビーカーに水を50 mL入れ温度変化を測定した例を図2-2に示す。 ホットプレートスターラーの天板とビーカーの間に水を張った場合の最終到達温度は79 °C、水を張らない場合は70 °Cであった。 ともに温度の時間変化は式 \eqref{eq:newtonln} に従うものとして解析でき、えられた緩和時間 1/k はそれぞれ 340 s、790 sであった。

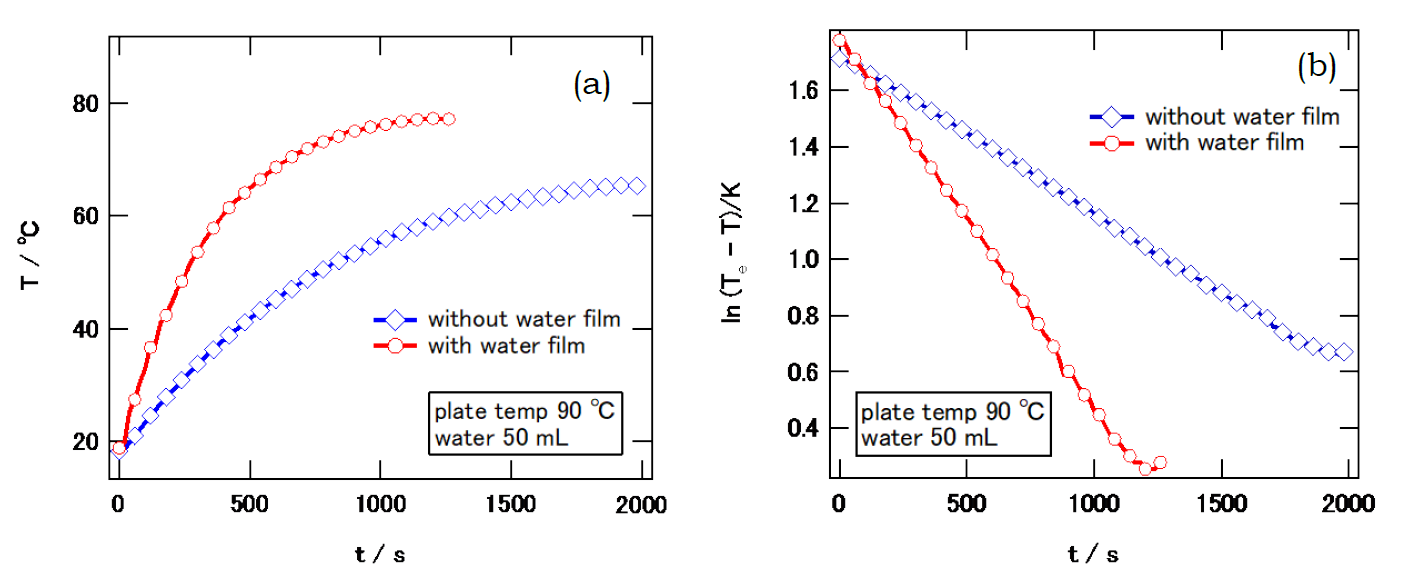
図2-2 ビーカーに入れた水をホットプレートスターラー上で加熱した時の温度変化。 100 mLのビーカーに水を50 mL入れてスターラーで撹拌。 (a) 温度変化の測定結果と(b) ニュートンの冷却則に従うと仮定した解析結果。 ln |T_X - T_e| は時間に対して直線的に変化し、直線の勾配から緩和時間が評価できた。