解説A: 分子のエネルギー構造
他の分子と相互作用していない孤立した分子の全エネルギー \(E\) は、 電子・振動・回転のエネルギーの和と考えることができる。
\begin{equation} E = E_\mrm{elec} + E_\mrm{vib} + E_\mrm{rot} \label{eq:molener} \end{equation}
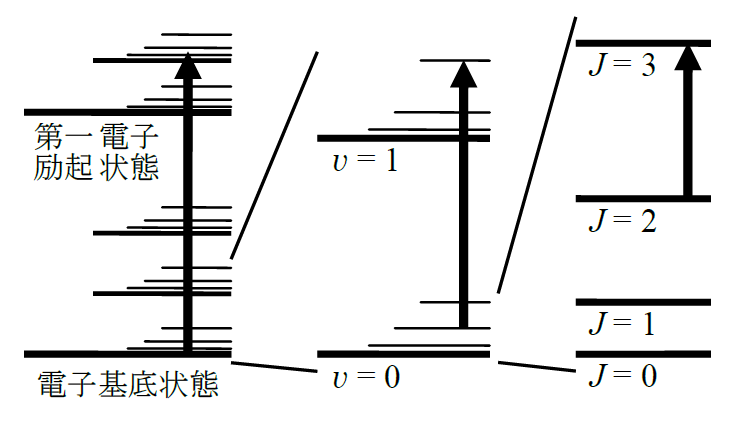
図1 分子のエネルギー準位構造の模式図
電子や原子が分子内に束縛されていて運動が定常的であるならば、 電子・振動・回転の各エネルギーは量子化されて離散的な値をとる。 これらのエネルギー値は分子種に固有のものであるが、 その大きさはどの分子種でもおおむね電子 >> 振動 >> 回転である。 電子・振動・回転のエネルギーの大きさが2桁程度ずつ違うため、 分子のエネルギー準位は、電子状態ごとに振動準位群が存在し、 さらに振動準位ごとに回転準位群が存在する階層構造となる(図1)。 図中の矢印は、左から電子振動回転遷移、振動回転遷移、純回転遷移を示している。 どの場合でも、遷移の始状態と終状態は固有の電子・振動・回転の量子数を持っている。 気相では周囲の分子との衝突頻度が小さいので、回転運動は実質的に定常状態とみなせて量子化され、 電子振動遷移や振動遷移に付随して回転準位間の遷移が観測される。 これに対して液相では、密度が高いため分子が自由に回転できず量子化された回転準位が消失する場合が多く、 ほとんどの分子の液相では電子振動遷移または振動遷移がもっぱら観測される。
解説B: 調和振動子のエネルギー準位
二原子分子の単純なモデルとして、質量\(m_1\)と\(m_2\)の質点が、質量ゼロで長さ \(r\) のバネで結ばれた系を考える。
古典力学ではバネ定数\(k\)のバネにつるされた質量\(m\)の質点は、 バネの自然長\(r_\mrm{e}\) からの変位に比例する復元力 \(f = - k (r - r_\mrm{e})\) によって、 角振動数(角速度)\(\omega = \sqrt{k / m}\)で単振動する。 二原子分子の振動が単振動として扱えるとして(調和振動子近似)シュレディンガー方程式を解くと、 量子化された振動エネルギー \(G(v)\) は波数 \(\tilde{\nu} = \nu/c = \omega / 2 \pi c\)を使って (\(c\)は真空中の光速、\(\hbar\) はプランク定数を \(2\pi\)で割ったもの \(h/2\pi\))
\begin{equation} G(v) = \hbar \omega \left(v + \frac{1}{2}\right) = hc \tilde{\nu} \left(v + \frac{1}{2}\right) \label{eq:enervib} \end{equation}
\begin{equation} \tilde{\nu} = \frac{1}{2\pi c} \sqrt{\frac{k}{\mu}} = 130.279 \sqrt{\frac{k / \mrm{(N~ m^{-1})}}{\mu/ \mrm{(g~ mol^{-1})}}} \mrm{cm^{-1}} \label{eq:wavenum} \end{equation}
\begin{equation} \mu = \frac{m_1 m_2}{m_1 + m_2} \label{eq:red_mass} \end{equation}
となり、エネルギー間隔は古典的振動数に対応する。ここで\(v~ (= 0, 1, 2, \ldots)\)は振動準位の量子数である。 二原子分子では結合(バネ)の両端に原子(質点)があるので、 各原子の質量\(m\)は式 \eqref{eq:red_mass} の実効質量 \(\mu\) として振動数に寄与する。
解説C: 赤外吸収と選択則
分子が吸収する光の振動数\(\nu\) は、始状態 \(| i \rangle \) のエネルギーを \(E_i\)、 終状態 \(| f \rangle\) のエネルギーを \(E_f\) とすると
\begin{equation} \hbar \omega = \Delta E = E_f - E_i \label{eq:abs_e} \end{equation}
のように、2つの状態のエネルギー差と等しいものに限られ、これを共鳴という。 つまり分子の吸収スペクトルは、分子種に固有の電子・振動・回転準位のエネルギー差を反映している。
分子1個が光を吸収または放出して始状態から終状態に遷移する確率は、 遷移モーメント \(\vec{\mu}\) の二乗に比例し、赤外吸収のような電気双極子遷移の場合、 電気双極子モーメントの演算子\(e\vec{r}\)により、
\begin{equation} \vec{\mu} = \langle f | e\vec{r} | i \rangle \label{eq:trans_moment} \end{equation}
である。ここで\(e\)は電荷、\(\vec{r}\) は位置の演算子である。 \(\langle f | e\vec{r} | i \rangle\) のブラケット表記は、状態 \(| i \rangle\) に 演算子\( e\vec{r}\) が作用した結果と状態 \(| f \rangle\) の複素共役の積を適当な座標で積分したものを表す。 すなわち、 \(\vec{\mu}\) の大きさは、遷移の始状態と終状態の性質によって決まる。 吸収や発光の絶対強度は、遷移強度 \(\vec{\mu}^2\) と始状態に存在する分子数\(N_i\)の積に比例し、 飽和がなければ吸収される光子数は入射光強度にも比例する。
振動準位\(v\)から\(v'\) への双極子遷移の強度は、 式 \eqref{eq:trans_moment} から、 電気双極子モーメント演算子\(e\vec{r}\)を始状態の波動関数\(| v \rangle\) に作用させ、 それと終状態の波動関数 \(| v' \rangle\) の積を核間距離\(r\)で積分した遷移双極子モーメント \(\vec{\mu} = \langle v' | e\vec{r} | v \rangle\) の二乗に比例する。 \(\vec{\mu}\) を平衡核間距離\(r_\mrm{e}\)のまわりでテーラー展開すると次のようになる (以下では簡単のため1次元の場合について示す)。
\begin{equation} \mu = \mu_\mrm{e} \langle v' | v \rangle + \left( \frac{\rmd \mu}{\rmd r} \right)_{r = r_\mrm{e}} \langle v' | r - r_\mrm{e} | v \rangle \label{eq:vv_trans} \end{equation}
ここで\(\mu_\mrm{e} \)は\(r = r_\mrm{e}\)での永久電気双極子モーメントを表し、 展開は一次微分までで打ち切っている。 各振動準位の波動関数は規格直交化されているので、式 \eqref{eq:vv_trans} の第1項において \(\langle v' | v \rangle = \delta_{v v'}\) となる。 したがって、異なる振動準位間の遷移には式 \eqref{eq:vv_trans} の第2項が寄与する。 第2項の積分は、調和振動子では\(\Delta v = v' - v = \pm 1\) のときにのみゼロとならない。 また第2項の\((\rmd \mu/\rmd r)_{r = r_\mrm{e}}\) は \(r_\mrm{e}\) 近傍での \(r\) の変化、 すなわち振動による電気双極子モーメントの変化を表す。 これら2つの因子の両方がゼロとならない条件から、振動遷移の選択則は次のようになる。
- 振動量子数の変化は \(\Delta v = \pm 1\)
- 電気双極子モーメントが振動によって変化
実際の分子では、上に述べたように完全な調和振動子ではないこと、 \(\mu\) のテーラー展開における二次微分以降の項の寄与等によって、 \(\Delta v = \pm 2\) 以上の遷移も弱い強度ながら観測される。 2番目の選択則により、分子のどのような振動運動が赤外吸収を示すかが理解できる(次項の解説参照)。 また、式 \eqref{eq:vv_trans} の二項目の係数から、 分子間相互作用によって分極が誘起された場合に赤外吸収強度が増大することも理解できる。
解説D: 分子の基準振動
二原子分子の振動を記述するハミルトニアンは、 平衡核間距離からのずれを振動座標 \(Q (= r - r_\mrm{e})\)として、調和振動子近似のもとで
\begin{equation} H_\mrm{vib} = \frac{1}{2} [\mu \dot{Q}^2 + k Q^2] \label{eq:vibH} \end{equation}
と書ける。 これを運動量形式に書き換えたシュレディンガー方程式を解くと、 式 \eqref{eq:enervib} の振動のエネルギー \(G(v)\) とそれに対応した固有関数 \(| v \rangle \) が得られる。
多原子分子の振動は二原子分子の振動とは異なり、 3つ以上の自由度(\(= n\)とする)を持つ。 この場合の振動の座標は、結合長や結合角の平衡位置からのずれになるが、 それらの一次結合をうまくとって新しい座標(基準座標)\(Q_1, Q_2, \ldots , Q_n \)を導入すると、 振動のハミルトニアンは
\begin{equation} H_\mrm{vib} = \frac{1}{2} [\mu_1 \dot{Q}_1^2 + k Q_1^2] + \frac{1}{2} [\mu_2 \dot{Q}_2^2 + k Q_2^2] + \cdots + \frac{1}{2} [\mu_n \dot{Q}_1^2 + k Q_n^2] \label{eq:vibHn} \end{equation}
と表される。このとき全振動エネルギーは各基準振動の振動エネルギーの和になる。
\begin{equation} G(v_1, v_2, \ldots, v_n)/\hbar = \omega_1 \left( v_1 + \frac{1}{2} \right) + \omega_2 \left( v_2 + \frac{1}{2} \right) + \cdots + \omega_b \left( v_n + \frac{1}{2} \right) \label{eq:enervibn} \end{equation}
ここで \(v_i\) と \(\omega_i\) は基準振動iの振動量子数と角振動数である。 この場合の固有関数は、各基準振動の波動関数の積 \(|v_1, v_2, \ldots, v_n \rangle = | v_1 \rangle | v_2 \rangle \ldots | v_n \rangle\)になる。
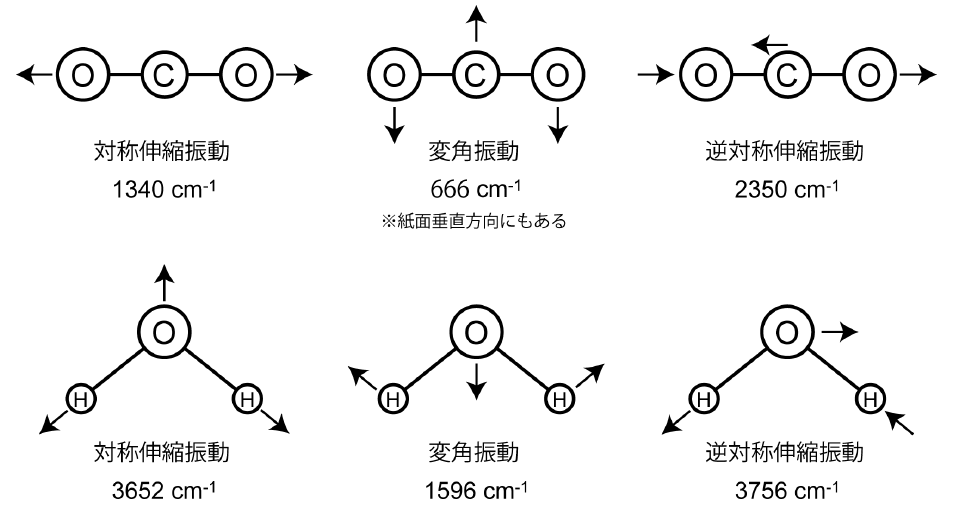
以下に基準振動の例として、直線三原子分子であるCO2、 および非直線三原子分子であるH2Oについて、その振動数とともに示す。
解説E: 多原子分子の振動と赤外吸収
原子数がN個の多原子分子について、すべての原子の位置を指定するには3N個の座標が必要であり、 これは運動の自由度の数に対応する。 そのうちの3個は重心の並進運動に対応し、さらにもう3個(直線分子の場合は2個)は回転運動に対応する。 したがって、残りの3N - 6個(直線分子では3N - 5個)が、 分子の骨格が変形する運動すなわち伸縮・変角などの振動運動に対応する。 多原子分子の振動は、これら3N - 6(= n)個の基準振動の問題として扱う必要があるが、 各結合に固有の伸縮振動や変角振動とみなせることが多い。 すなわち伸縮振動については、結合の両端の原子のみに着目し、これを二原子分子と同様に扱える。
例えばメタノール CH3OHでCH伸縮、CO伸縮、OH伸縮の3種類の伸縮振動にのみ注目してみよう。 この近似ではCH3基の3つのCH結合は区別されないが、 複数の等価な結合の伸縮振動は、 それらが同じ位相で振動する対称伸縮振動と逆の位相で振動する逆対称伸縮振動に分かれる。 一般の取り扱いは厄介だが CO2ような直線XYX型分子の対称伸縮振動と逆対称伸縮振動の振動数は XY結合のバネ定数を\(k\)、 原子XとYの質量を\(m_\mrm{X}\)、\(m_\mrm{Y}\) として次のように表される。
\begin{equation} \omega_\mrm{sym} = \sqrt{k/m_\mrm{X}} \label{eq:XYXsym} \end{equation}
\begin{equation} \omega_\mrm{asym} = \sqrt{k (m_\mrm{Y} + 2m_\mrm{X})/m_\mrm{X} m_\mrm{Y}} \label{eq:XYXasym} \end{equation}
式 \eqref{eq:XYXsym} と式 \eqref{eq:XYXasym} 式の比をとると、 大きさは \(m_\mrm{X}\) と \(m_\mrm{Y}\) の比に依存するが、 常に \(\omega_\mrm{asym} \gt \omega_\mrm{sym} \) で逆対称振動の振動数が大きいことがわかる。
遷移強度や選択則についても、多原子分子では基準振動を扱わねばならないが、 結果的には二原子分子の議論と同様に考えてよいことがわかる。 すなわち双極子モーメントが変化する振動について赤外吸収遷移が観測される。 調和振動子近似において述べた選択則を多原子分子に拡張すると、次のようになる。
- 始状態から終状態で、ある1 つの基準振動の量子数のみ \(\Delta v = \pm 1\) 変化
- 電気双極子モーメントが基準振動によって変化
選択則の (1) については、解説Bで述べた調和振動子近似の破れ、 あるいは\(\mu\) のテーラー展開における二次微分以降の項の寄与等によって、 多原子分子でもある基準振動が \(\Delta v = \pm 2\) 以上となる遷移(倍音)や、 複数の基準振動の量子数が変化する遷移(結合音)が弱い強度ながらも観測される。 選択則の (2) は、群論の表現を使うと、 始状態と終状態の既約表現の積が\(x, y, z\)のどれか1つと同じ既約表現となることが要求されるということである。 これは式 \eqref{eq:vv_trans} の積分がゼロにならない条件を群論で表現したもので、 終状態・双極子モーメントのベクトル成分・始状態の3つの既約表現の積が全対称表現になる条件である。
解説F: 二原子分子の回転エネルギー準位
古典力学では、慣性モーメント\(I\)の棒状剛体が角運動量 \(J = I \omega\) で回転するエネルギーは \(J^2 /2I\)で表される。ここで\(\omega\)は回転運動の角振動数を表す。 慣性モーメントは \(I = \sum m_i r_i^2\) (\(r_i\) は回転軸からの距離)で定義され、 物体の回転のしやすさを表す。 直線運動では運動量\(P = mv\)、運動エネルギー\(E = P^2/2m\) であるから、 \(I \Leftrightarrow m\)、\(\omega \Leftrightarrow v\)、\(J \Leftrightarrow P\) の対応がある。 角運動量演算子\(\vec{J}^2\)の量子力学的期待値は\(J(J + 1) \hbar^2/2\)なので、 離散的な回転エネルギーは
\begin{equation} E_\mrm{rot} = \frac{J (J + 1) \hbar^2}{2I} \label{eq:ener_rot} \end{equation}
となる。ここで \(J (= 0, 1, 2, \ldots)\) は回転角運動量の量子数である。 二原子分子の場合には慣性モーメント\(I\)は次のように書き換えられる。
\begin{equation} I = m_1 r_1^2 + m_2 r_2^2 = \mu r'^2 \label{eq:m_inertia} \end{equation}
ここで \(r_1, r_2\) は重心から各原子への距離(\(r' = r_1 + r_2\) )、\(\mu\) は実効質量である。 振動の場合と同様に波数単位に書き直すと
\begin{equation} F(J) = B J (J + 1) \label{eq:rot_eneJ} \end{equation}
\begin{equation} B = \frac{\hbar}{4 \pi c I} \label{eq:rot_const} \end{equation}
となる。ここで\(B\)は回転定数と呼ばれ、慣性モーメントの逆数に比例する (回転定数をエネルギー単位で表現する場合には\(B = \hbar^2/2I\) となる)。
ここまでの議論では、分子内の核間距離は一定として考えてきた(剛体回転子近似)。 しかし実際の分子は振動しながら回転しているので、核間距離は一定ではない。 二原子分子についてこの振動回転相互作用の効果を考えると、 式 \eqref{eq:rot_const} の回転定数は振動準位ごとに異なる値をもち、 振動準位 \(v\) における回転定数 \(B_v\) は良い近似で
\begin{equation} B_v = B_\mrm{e} - \alpha_\mrm{e} \left( v + \frac{1}{2} \right) \label{eq:Bv_dependence} \end{equation}
と書ける。ここで \(B_\mrm{e}\)は平衡核間距離における回転定数、 \(\alpha_\mrm{e}\) は振動回転相互作用の定数で一般に正の値をとる。
古典力学において、ばねで結ばれた二つのおもりの回転を考えると、 回転速度が大きくなると共におもり間距離が伸び、慣性モーメントが大きくなる。 この効果は遠心力ひずみと呼ばれ、角運動量の4乗に比例して回転エネルギーが小さくなる項が加わる。 量子力学的には、この効果は
\begin{equation} F(J) = B_v J (J + 1) - D_v J^2 (J + 1)^2 \label{eq:centrifugal} \end{equation}
のように2項目の遠心力項として現れる。 これは 式 \eqref{eq:rot_eneJ}において回転定数 を回転準位に依存した実効的な回転定数
\begin{equation} B_\mrm{eff}(J) = B_v - D_v J(J+1) \label{eq:rot_eff} \end{equation}
に置き換えたとみることもできる。 遠心力ひずみ定数\(D_v\)の大きさはおよそ\(4 B_\mrm{e}^3/\omega_\mrm{e}^2\) であり、 一般に高い回転準位でなければ遠心力項の影響は小さいが、 塩化水素のように水素原子を含む二原子分子では低い回転準位でも影響があらわれる。
解説G: 二原子分子の振動回転遷移
回転準位\(J\) から\(J'\) への双極子遷移の選択則は \(\Delta J = J' - J = 0, \pm 1\)であり、 \(\Delta J = -1, 0, +1\) の遷移を各々P枝、Q枝、R枝と呼ぶ。 塩化水素の振動回転遷移ではP枝とR枝のみが許容である。 遠心力ひずみを無視すれば、 R枝とP枝の遷移エネルギーの波数\(\tilde{\nu}_\mrm{R}\) と\(\tilde{\nu}_\mrm{P}\)は 始状態の回転量子数 \(J\) の関数として
\begin{equation} \tilde{\nu}_\mrm{R} = \tilde{\nu}_0 + B' (J + 1)(J + 2) - B J(J + 1) = \tilde{\nu}_0 + (B' + B) (J + 1) + (B' - B) (J + 1)^2 \label{eq:Rbranch} \end{equation}
\begin{equation} \tilde{\nu}_\mrm{P} = \tilde{\nu}_0 + B' J(J - 1) - B J(J + 1) = \tilde{\nu}_0 - (B' + B) J + (B' - B) J^2 \label{eq:Pbranch} \end{equation}
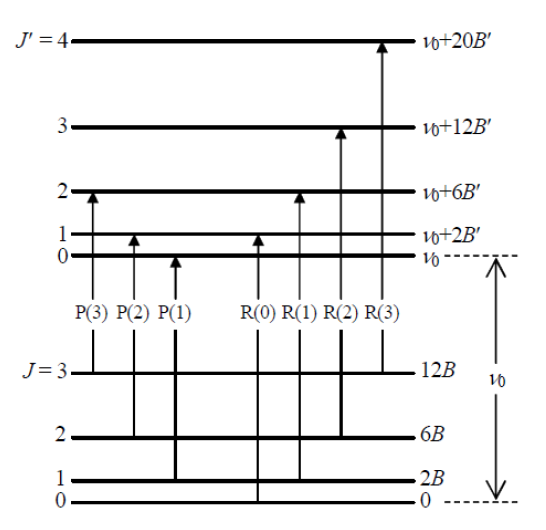
図2 二原子分子の振動回転遷移
となる(右図2参照)。 ここで\(B’\)とBは吸収の終状態と始状態の回転定数、 \(\tilde{\nu}_0\) は2つの振動準位の の準位間のエネルギー差に対応する波数である。 まず簡単のため回転定数が振動準位に依存しない場合(\(B’ = B\)の場合)を考えると、 式 \eqref{eq:Rbranch}、\eqref{eq:Pbranch} の最後の項は消えるため、 回転線は \(2B\) の等間隔で並ぶ。 \(J\)の最小値は0なのでR枝は \(J = 0\)から始まり、P枝は\(J = 1\)から始まる。 \(B’ = B\)より\(\tilde{\nu}_\mrm{R}(0) - \tilde{\nu}_\mrm{P}(1) = 4B\)となるので、 R枝とP枝の始まりの間隔は他の回転線の間隔の2倍になる。 以上に留意すれば振動回転線の帰属は容易である。
実際の回転定数は振動準位によって異なるので、 次に\(B’ \ne B\)の一般の場合を考える。 式 \eqref{eq:Rbranch}、\eqref{eq:Pbranch} の最後の項により回転線は等間隔ではなくなる。 このとき回転線の間隔は\(J\)に対して滑らかに変化し、 \(B’\)と\(B\)の大小関係に応じて、P枝とR枝のうち一方は間隔が狭くなり他方は広くなる。 \(B’\)と\(B\)は
\begin{equation} \tilde{\nu}_\mrm{R}(J) - \tilde{\nu}_\mrm{P}(J) = 2B' (2J + 1) \label{eq:RPjj} \end{equation}
\begin{equation} \tilde{\nu}_\mrm{R}(J-1) - \tilde{\nu}_\mrm{P}(J+1) = 2B (2J + 1) \label{eq:RPjmjp} \end{equation}
の関係から \(\Delta J\)が異なる回転遷移の遷移エネルギーの差から決定できる。 この方法は結合差法と呼ばれ始状態または終状態の一方の回転定数が消去されるため解析が容易になる。 この場合、回転定数によらず同じ回転定数が得られるが、 本実験で扱う塩化水素の場合、前述のように式 \eqref{eq:centrifugal} の遠心力項が無視できないため、 回転定数は回転量子数に依存する。 遠心力項を考慮すると結合差は
\begin{equation} \tilde{\nu}_\mrm{R}(J) - \tilde{\nu}_\mrm{P}(J) = (2B' - 3D') (2J + 1) - D'(2J + 1)^3 \label{eq:RPjj_c} \end{equation}
\begin{equation} \tilde{\nu}_\mrm{R}(J-1) - \tilde{\nu}_\mrm{P}(J+1) = (2B-3D) (2J + 1) - D(2J + 1)^3 \label{eq:RPjmjp_c} \end{equation}
となる。この場合でも\(B \gt \gt D\)より、 \((2B - 3D) \approx 2B\)とおいて両辺を\(2(2J + 1)\)で割れば
\begin{equation} (\tilde{\nu}_\mrm{R} - \tilde{\nu}_\mrm{P})/2(2J + 1) =B - D(2J + 1)^2 /2 \label{eq:RPjjx} \end{equation}
となり最小二乗解析から振動準位ごとに回転定数\(B\) (\(B’\))と遠心力ひずみ定数\(D\) (\(D’\))が決定される。
解説H: 振動回転線の強度分布と温度
P枝、R枝を構成する回転線の強度は、 振動のみのエネルギー変化\(h \nu_\mrm{vib}\)から離れた2箇所で最大強度を示す特徴がある。 これはおよそ吸収強度が遷移始状態の占有確率に比例すると考えると説明できる。 回転準位は\(2J + 1\)の縮重度を持つ。 そして、ボルツマン分布に従って基底振動状態の回転準位は予め熱励起されている。 すなわち基底振動状態の回転準位はおおよそ
\begin{equation} (2J + 1) \exp \left[ -\frac{B J(J + 1)}{k_\mrm{B} T} \right] \label{eq:Jdistr} \end{equation}
に比例した占有確率を示すと考えられる。 この関数は\((2J + 1)\)因子の影響で一旦増加するが指数関数部分の影響で大きな\(J\)では0に近づく。