＜概要＞

pH計は水素イオン濃度の異なる溶液間の電位差を測定することでpHを測定する。 ここではその基礎となる知見を得るため、濃度の異なる硝酸銀溶液間の電位を、金属銀を電極として測定する実験を半定量的なレベルで行う。

＜試薬＞

以下の試薬はいずれも用意してあるものを使用する。

1. 0.10 mol/L硝酸銀溶液
2. 0.10 mol/L硝酸カリウム溶液
3. 0.10 mol/L塩化カリウム溶液

＜操作＞

1. 空のサンプル管を３本用意し、その内１本（イとする）に0.10 mol/L硝酸銀溶液を0.30 g取り、0.10 mol/L硝酸カリウム溶液を加えて3.0 gにして振り混ぜる。
2. イの硝酸銀溶液を0.30 g、空のサンプル管（ロとする）に取り、0.10 mol/L硝酸カリウム溶液を加えて3.0 gにして振り混ぜる。 同様にロの硝酸銀溶液（0.001 mol/L）を0.30 g取って硝酸カリウム溶液で10倍に希釈した溶液をサンプル管に作る（ハとする）。
   
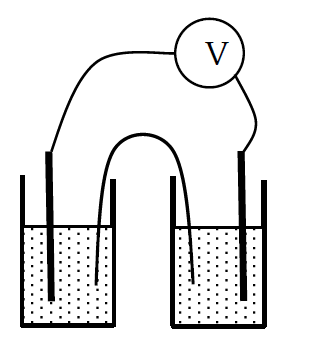
3. 用意されている銀線を洗浄した後、ロとハに浸し、マルチメータU1251Aのプローブを銀線に接続する。
4. ろ紙を細長い短冊状に切り、ロとハのサンプル管に浸す（右図参照）。 ろ紙にそれぞれの硝酸銀溶液が浸み込み、電気が流れる状態になったら電圧の表示が落ち着くはずなので、 それを読み取る（マルチメータは～1000 mVレンジにして測定する^*1。1 mV程度までの精度でよい）。 なおこの時、ロの液面がハの液面よりも高いとサイフォンが働いて、濃度の高いロの溶液がハに流入してきて濃度が大きく変わることがあるので、 液面の高さをほぼそろえるようにする。
5. （４）と同様の測定を、イとハ、イとロについても行う。 電極を異なる濃度の溶液に入れる時は、ろ紙で電極表面を拭い、イオン交換水でよく洗浄し清浄にしておく。
6. イとロを（４）の設定にして電圧を測りながら、用意してある0.10 mol/L塩化カリウム溶液を0.2 mL、ロに混ぜ加えて塩化銀を生成させ、 電圧がいくらになるかを測る。さらに0.10 mol/L塩化カリウム溶液を0.2 mL、ロに混ぜ加えて電圧がいくらになるかを測る。

^*1 U1251Aの50～1000 mVレンジでの内部抵抗は1 GΩ 以上、5～1000 Vレンジの入力インピーダンスは10 MΩ とされている。 レンジを切り替えた時に表示される電圧が変化するかどうか調べてみよ。 より精密な測定にはポテンショスタットと呼ばれる構成・装置を用いて電流値が 0 になる電位差を測定する手法が用いられる。

＜解説＞：濃淡電池の電位

サンプル管AとBに銀線を浸して電圧を測る時、銀線の表面では

Ag⁺ + e^- → Ag

という反応が起き、同時にAとBの間でイオンのやり取りが起きる。 かりに q F だけの電荷が電圧計を通じてAからBに移動したとすると（F はファラデー定数 ≅ 9.65 × 10⁴ C mol^-1）、 ろ紙の短冊を介して t_Ag q の銀イオンと t_K q のカリウムイオンが B から A に、 t_NO3 q の硝酸イオンが A から B に移動し、銀イオン濃度はA中では (1 - t_Ag) q 減少し、B中では(1 - t_Ag)q 増加する。 今回の実験条件ではカリウムイオン濃度は銀イオン濃度より十分大きくt_K ⟩⟩ t_Ag ∼ 0で、 また A と B 中のカリウムイオンと硝酸イオン濃度は等しいとみなせるので、 測定される電圧 E は Nernst の式を用い次式で表される（Rは気体定数、Tは熱力学温度、|Ag⁺|は銀イオンの活量）：

\begin{equation} E = \frac{RT}{F} {\ln \rm{ \frac{|Ag^+|_B}{|Ag^+|_A}}} \approx \frac{RT}{F} \ln \frac{c_{\rm{B}}}{c_{\rm{A}}} \label{eq:Nernst} \end{equation}

室温付近では

\begin{equation} E \approx \frac{RT}{F} \ln \frac{c_{\rm{B}}}{c_{\rm{A}}} \approx 59 {\rm{~mV}} \times \log \frac{c_{\rm{B}}}{c_{\rm{A}}} \label{eq:NernstX} \end{equation}

ここで B に塩化カリウム溶液を十分量加えると塩化銀が沈殿し、 この時の銀の濃度は塩化銀の溶解度積を pK_s (= - log K_s = - log [Ag⁺][Cl^-]) とすると次式で与えられる：

\begin{equation} \log {\rm{[Ag^+]_B} = -p} K_{\rm{s}} - \log {\rm{[Cl^-]_B}} \label{eq:solProduct} \end{equation}

この場合の電位差は塩化物イオンが加わって事態は複雑だが、おおむね次式が成り立つことが期待される：

\begin{equation} E = \frac{RT}{F} {\ln \rm{ \frac{|Ag^+|_B}{|Ag^+|_A}}} \approx E_{\rm{BA}} - (59 {\rm{~mV}}) \times (\log c_{\rm{B}} + {\rm{p}} K_{\rm{s}} + \log \rm{[Cl^-]_B}) \label{eq:NernstY} \end{equation}

ここで E_BA は塩化カリウムを入れる前の電位差である。 この関係を用い、測定される電位の値を用いて塩化銀の溶解度積を評価できる。

＜検討＞

1. イ、ロ、ハそれぞれの間の電位差について式 \eqref{eq:NernstX} が成立するか確認せよ。
2. 塩化カリウムを加えた場合の電位差から塩化銀の溶解度積を評価し、文献値（pK_s = 9.75）と比較せよ。
3. サンプル管同士を連結するのに、ろ紙ではなく銀線を用いたら電位差はどうなるか予想し実際にやってみよ。
4. 硝酸カリウム溶液ではなくイオン交換水で硝酸銀溶液を希釈して濃淡電池を構成したら、どのような結果が得られるだろうか？
5. 式 \eqref{eq:NernstY}の関係を利用すれば、電位差を測定することで塩化物イオンの濃度を知ることができることになる。 どれくらいの濃度まで塩化物イオンの濃度を測定できるだろう？