<概要>
屈折率は迅速・容易に精度よく測れ、糖度、塩分をはじめ、組成が知れた溶液の濃度をモニターするのに幅広く利用されている。 ここではポケット屈折計 PAL-RI(アタゴ社製)を用いて、 シクロヘキサン(nD20 = 1.427)とトルエン(nD20 = 1.496)の混合溶液の屈折率の濃度依存性を調べ、 濃度未知の溶液の濃度を決定する(nD20 はナトリウムのD線(589 nm)に対する20 °Cにおける屈折率)。 屈折計 PAL-RIの精度は±0.0003程度(分解能は0.0001)なので、今回の混合系の組み合わせでは、 およそ ±1 % の精度で組成の決定が可能である。 なおポケット屈折計 PAL-RIの筐体はABS樹脂でできており トルエンなどの溶剤に侵される。 測定に当たっては、溶液が筐体に付かないように注意する。
<操作>
- サンプル管(3 mL)を4本用意し、シクロヘキサンをそれぞれ0.2、0.4、0.6、0.8 gずつ0.01 gの桁まで読んではかり取り、 それぞれにトルエンを0.8、0.6、0.4、0.2 gを同様に0.01 gの桁まで読んではかり取って加え、よく振り混ぜる。
- ポケット屈折計 PAL-RIを用いて、純シクロヘキサン、純トルエン及び(1)で調製した混合溶液の屈折率を測定する (それぞれ試料溶液0.3 mL程度を要する。これより少ないと測定値が不安定になる)。
- 屈折率に温度補正を施して25 °C(実験当日の気温に合わせて設定すればよい)の値に換算し、 横軸にシクロヘキサンの質量分率mを、縦軸に25 °C換算の屈折率を取って検量線を作成する。
- 用意してある未知試料について屈折率を測定し、未知試料中のシクロヘキサンの質量分率を決定する。
<データ処理>
- トルエン等の有機溶媒では温度が1 °C上がると、屈折率は0.0005程度下がる。
アイクマン Eykman の式(資料編II-14参照)を用いると、温度 δt の変化にともなう屈折率変化 δntは、
温度変化が数 °C 程度であれば液体の膨張率を 1.1 × 10-3 K-1として次式で評価できる*1:
δnt = -1.2 × 10-3 (n - 1.02) δt (1)
一般に温度を下げる( δt < 0)と屈折率は大きくなり(δnt > 0)、 式 (1) を用いると、たとえば23 °Cで屈折率 n が1.4480 のとき25 °C換算の屈折率は1.4467となる。 なお屈折率計が表示する温度は屈折率計本体の温度なので、0.1 °Cまでの分解能で表示されていてもあまり高い精度は望めないことに注意する(PAL-RIの古い機種の分解能は1 °C)。*1 アイクマンの式から δnt = [(n2 - 1)(n + 0.4)/(n2 + 0.8n + 1)] αP δt が得られ (αP は膨張率(1/V)(∂V/∂t)P)、 n ≈ 1.4 程度であれば -(1.10n - 1.12) αP δt と近似できる。
- シクロヘキサン-トルエン混合液体の屈折率nは、シクロヘキサンの質量分率 m に対し若干の非線形性を示す。
測定した未知試料の屈折率に相当する質量分率の値を検量線のグラフから直接読み取ってもよいが、
ここではその非線形性の影響を
n = n2 + (n1 - n2)m + k m (1 - m) (2)
というかんたんな式に最小2乗法を用いて当てはめることで評価することを考えよう (n1は純シクロヘキサン n2 は純トルエンの屈折率、 kは実験的に決める係数)。 δn = n - [n2 + (n1 - n2) m ] が m (1 - m) と比例関係にあるものとして最小2乗法を適用して係数 k は決めればよい。 図6-1に典型的な実験結果を示す:このようにして得られた実験式 n = n2 + (n1 - n2)m + k m (1 - m) を用い、 実験的に得られる屈折率 n から質量分率 m を求めるには2次方程式の根の公式を用いてもよいが、今回の場合は非線形項が小さく、 m の精度を考えると逐次近似法を用いるのが簡便である。 単純な逐次近似法ではまず第0近似として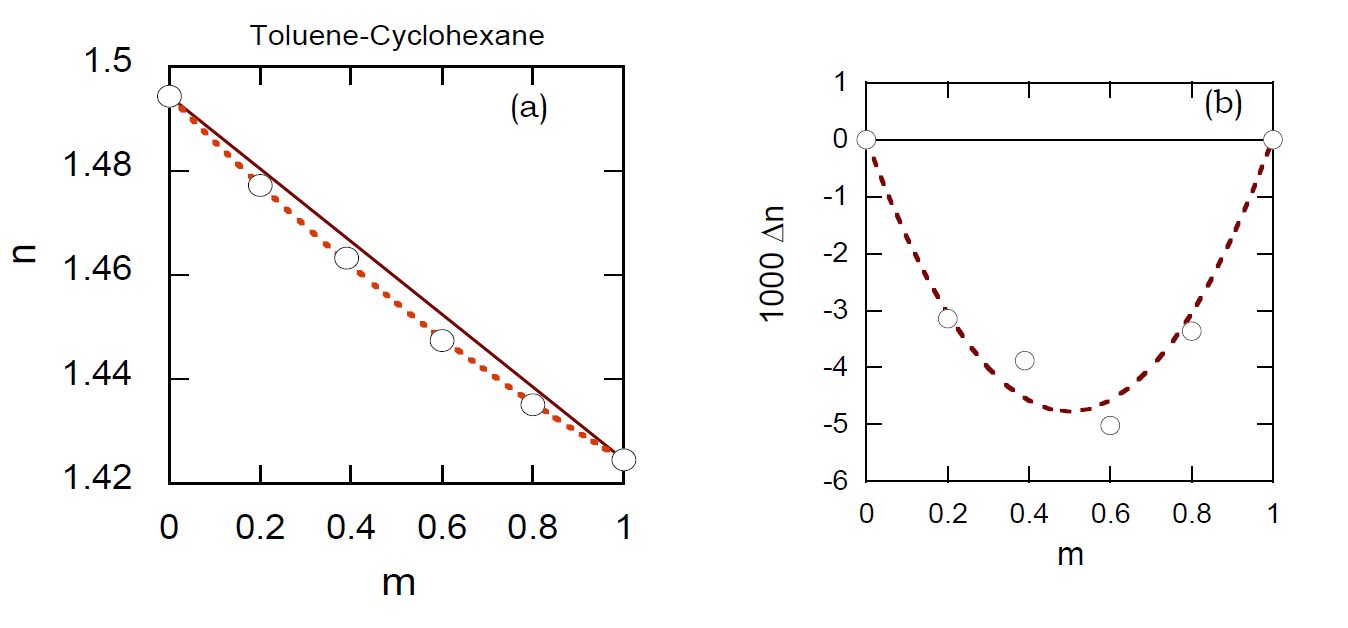
図6-1. シクロヘキサン-トルエン混合物の屈折率の検量線の実験例。 (a) 25 °C 換算の屈折率 n は質量分率 m に対し負の偏倚を示し、 (b) 偏倚はおおむね k m (1 - m)という関数で評価できた。
m(0) = (n - n2)/(n1 - n2) (3)
をとり、第 1 近似: m(1) = m(0) - [k/(n1 - n2)] m(0)(1 - m(0))
という風に計算を進めていく。 今回の場合は第1近似ぐらいまでで十分であろう*1。
第 2 近似: m(2) = m(0) - [k/(n1 - n2)] m(1)(1 - m(1))
第 3 近似: m(3) = m(0) - [k/(n1 - n2)] m(2)(1 - m(2))
・・・・
*1 今回の場合は非線形項が2次関数なので根の公式で容易に解くことができるが、 もっと複雑な非線形項を持つような場合にもこの逐次近似の方法は適用可能である。 ただし非線形項が大きくなってくると逐次近似が収束しなくなってくるので注意が必要。
<検討>
- シクロヘキサン-2-プロパノール(nD20 = 1.378)についても検量線を作成してみよ。