<概要>
シクロヘキサン(沸点80.7 °C)とトルエン(沸点110.6 °C)の混合液体の沸点-組成曲線を図6-2に、 液相(x)-蒸気組成(y)曲線を図6-3に示す。
 |
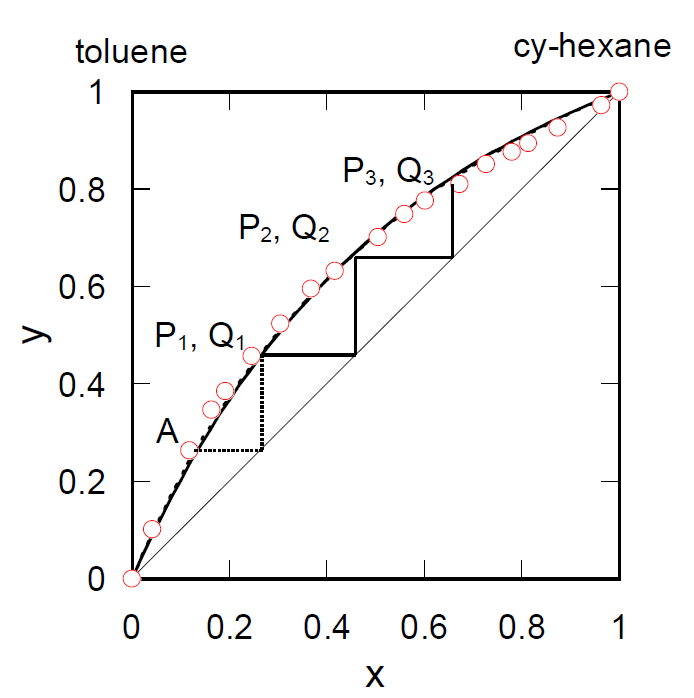 |
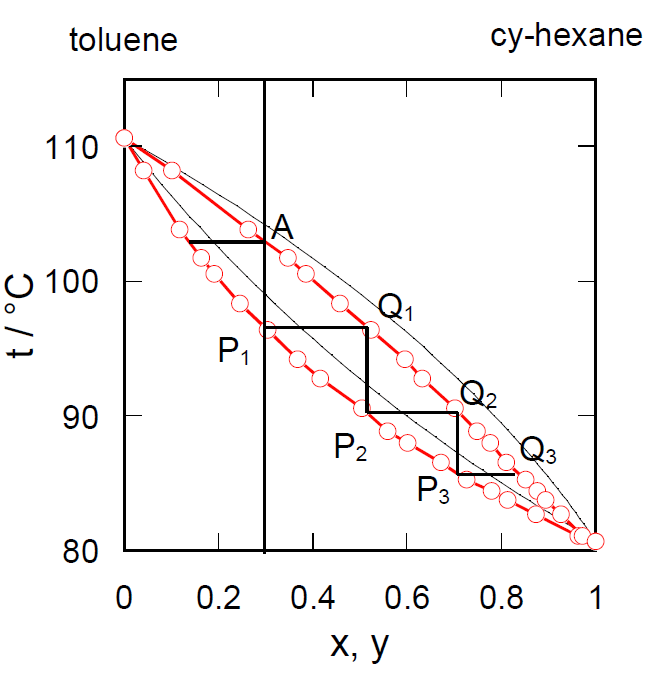
| 図6-2 シクロヘキサン-トルエン系の沸点組成曲線。図中細い実線は理想溶液近似による計算値。 | 図6-3 シクロヘキサン-トルエン系の液相蒸気組成曲線。図中細い実線は理想溶液近似による計算値。 点線(ほとんど重なっている)は相対揮発度を一定とした計算値。 |
仮に内容積が可変のピストン-シリンダー装置の中にシクロヘキサンのモル分率 x = 0.30 の混合液体を入れ、 圧力を1気圧に保って温度を上げていくとしよう。 温度を上げていくと図6-2のP1 で沸騰が始まって蒸気相 Q1が出現し、 蒸発が進むに従って液相が減り蒸気相が増えて、A点に至ってすべて蒸気相で占められるようになる。 蒸気相の組成は y = 0.50(液相のモル分率をx、蒸気相のモル分率をyとする)から小さくなって A では y = 0.30、液相組成は x = 0.16となる。
実験室的な蒸留操作の場合には、加熱しながら蒸気をそのつど凝縮させ系から取り除くことになるので事態はいささか複雑である。 発生した蒸気が逐次すべて液体として回収されたとすると、次のレイリーRayleighの式が成立する:
\begin{equation} \ln \frac{B_0}{B} = \int_x^{x_0} {\frac{\rmd x}{y - x}} \label{eq:Rayleigh} \end{equation}
ここで B は液相の物質量(あるいは質量)、x、yはそれぞれ液相、蒸気相中の注目する成分(成分1)のモル分率(あるいは質量分率)である。 仮に凝縮する蒸気が液相と平衡にあるとしよう(単蒸留simple distillation)。 取り扱いを容易にするため、溶液が理想溶液と見なせ、 相対揮発度 \(\alpha = P_1^\bullet /P_2^\bullet\)(純粋な状態での成分1と2の蒸気圧の比)が温度によらず一定であるとすれば、 留出液の組成(つまり蒸気相の組成 y)と液相の組成 x の間には次の関係が成り立ち、
\begin{equation} y = \frac{\alpha x}{1 + (\alpha - 1) x} \label{eq:idealsol} \end{equation}
レイリーの式は次式のように表される:
\begin{equation} \ln \frac{B_0}{B} = \frac{1}{\alpha - 1} \ln \frac{x_0}{x} + \frac{\alpha}{\alpha - a} \ln \frac{1 - x}{1 - x_0} \label{eq:Rayleigh_id} \end{equation}
単蒸留で得られたモル分率 0.50 の留出液をもう一度蒸発させると、 今度は P2で沸騰が始まり Q2 の組成(モル分率約 0.70)の留出液を得ることができ、 さらに Q2の組成の留出液を蒸発させると P3で沸騰が始まり Q3の組成(モル分率約0.85)の留出液を得る。 実際に用いる蒸留装置ではこうした過程が起きる結果、単蒸留で期待されるよりは一般に分離の効率は高くなる。 あるいはフラスコ内の沸騰温度は留出温度より低い。 相対揮発度が一定で理想溶液として扱うことができれば、 このような蒸発・凝縮のプロセスを n 回繰り返して得られる蒸気相の組成は次式で与えられる(フェンスケFenskeの式):
\begin{equation} y = \frac{\alpha^n x}{1 + (\alpha^n - 1) x} \label{eq:Fenske} \end{equation}
つまり単蒸留の場合に用いた相対揮発度 \(\alpha = P_1^\bullet /P_2^\bullet\) を実効的な相対揮発度 \(\alpha_{\rm{eff}} =\alpha^n\) に置き換えることで、 蒸留による分離の見通しを得ることができる。 こうした分離プロセスにおいて理論段数 number of theoretical plates といわれるものは、この n に相当する。 蒸発・凝縮の過程を連続的に何度も行うことで効率的に分離を行う分留操作を精留 rectification と呼び、 種々の精留装置(精留塔)が用いられている。
<操作>
- 用意してあるアルミ製カップに半ば程度までグリセリンを入れ、 加熱のためのグリセリン浴を用意する。 グリセリン浴には撹拌子を入れ、ホットプレートスターラー上で撹拌ができるようにしておく(注1)。
- 100 mLの三口フラスコにシクロヘキサンとトルエンをそれぞれ 15 g程度ずつ、 0.01 gまで精確に秤量して入れる(量比は適宜変えてよい)。
- 三口フラスコに撹拌子を入れてト字管と冷却管を取りつけ、 三口フラスコをグリセリン浴に浸けてホットプレートスターラー上で加熱して蒸留を行う(注2)。 留分をおよそ 2~3 g 程度ずつの分画に分けてサンプル管に採取し、 留出温度およびフラスコ内温度を記録する(注3)。
- フラスコ中の残液がわずかになったら蒸留をやめ、残液を回収する(ト字管や冷却管等に付着しているものまで回収する必要はない)。
- 得られたそれぞれの留分分画および蒸留残液の屈折率を測定して組成を求める。
(注2)グリセリン浴とフラスコ内の混合液体を同時に撹拌子で撹拌する形になる。 グリセリン浴の温度は混合液体の沸点より10~20 °C高く保つ必要がある。 蒸留が進むにつれ留出温度が上がるのに合わせてグリセリン浴の温度を少しずつ上げ、留出速度があまり落ちないようにする。
(注3)留出温度の測定にはガラス温度計ではなく、浸没の補正が不要で温度変化の応答性にすぐれたデジタル温度計を使用する。 デジタル温度計の筐体はトルエン等の有機溶剤に侵されるので筐体にトルエンを付けたりしないように注意する。 ト字管の部分はアルミホイルを巻いて保温し、デジタル温度計の測温部(ステンレス管先端部)は留出蒸気の中心部に来るようにセットする。 フラスコ内の沸騰温度を測定する温度計の測温部は、必ずしも蒸留母液中に浸っている必要はないが、できるだけ蒸留母液に近い位置にセットする。
<実験結果の解析・データ処理>
- モル分率のかわりに質量分率を用いても式 \eqref{eq:idealsol}、\eqref{eq:Rayleigh_id} 同様の式が成立することを確認せよ。
- 留出総量と蒸留残液量から、仕込んだ混合液体から揮散あるいは器具に付着するなどして未回収になった量を求めよ。 未回収の量が仕込みの1割以上ある場合は、蒸留装置のすりの部分からの漏れ等が疑われるので、 教員・TAとも相談し、実験をやり直すことを薦める。
- 留出液の組成と留出温度の関係をプロットし、気液共存状態についての文献値と比較せよ (平衡蒸気組成yと温度の関係と比較すればよい。両者はほぼ一致するはずである。 文献値は別途配布するものを利用すればよい)。
- それぞれの留液の分画を採取した時のフラスコ中の沸騰温度から、
平衡液組成 x と温度に関する文献値を用いて、フラスコ中の溶液の組成を求めよ
(シクロヘキサンのモル分率 x の時の沸点を tb(x) °Cとすると、
tb(x) = tb(1) x + tb(0) (1 - x) - 30.6 x(1 - x)(1 - 0.60x)
で近似できることから逐次近似法等で求めてもよいし、グラフを書いて読み取ってもよい)。 - ある留液の分画に対応するフラスコ中の溶液のシクロヘキサンの質量分率 m は、
各留液分画の重さ \(w_i\)とシクロヘキサンの質量分率 \(m*_i\) がわかっておれば次式でも評価できる:
\begin{equation} m = \frac{B_0 m_0 - \sum_i {w_i m_i^*}}{B_0 - \sum_i {w_i}} \label{eq:m_cumul} \end{equation}
ここで \(B_0\) と \(m_0\) は最初に仕込んだ溶液の重さとシクロヘキサンの質量分率である。 こうして求めたフラスコ中のシクロヘキサン濃度と(4)で求めた濃度が一致するか検討せよ。 - ト字管を用いた蒸留が単蒸留であるなら、フラスコ内の温度と留出温度は一致するはずだが実際には一致しない (フラスコ中の混合液体の質量分率が 0.5 程度なら、フラスコ内の沸騰温度は 90 °C程度だが、 留出温度はそれより5 °C 程度低くなるであろう)。 蒸留が進むにしたがって、フラスコ内の温度と留出温度の差がどのように変化するか図示せよ。
- フラスコ中の液相組成xと留出組成(蒸気組成)y から 式\eqref{eq:Fenske}に基づいて実効的な相対揮発度 \(\alpha_{\rm{eff}}\)を評価し、 レイリーの式に基づいて留出量(未回収量は無視する)と留出液組成(蒸気組成)yの関係を求め、実験結果と比較せよ。
<実験例>
シクロヘキサン-トルエン混合液体(シクロヘキサンの質量分率0.50)30.00 gを蒸留した実験例を図6-4に示す (蒸留終了時残液量0.53 g。未回収量1.89 g)。
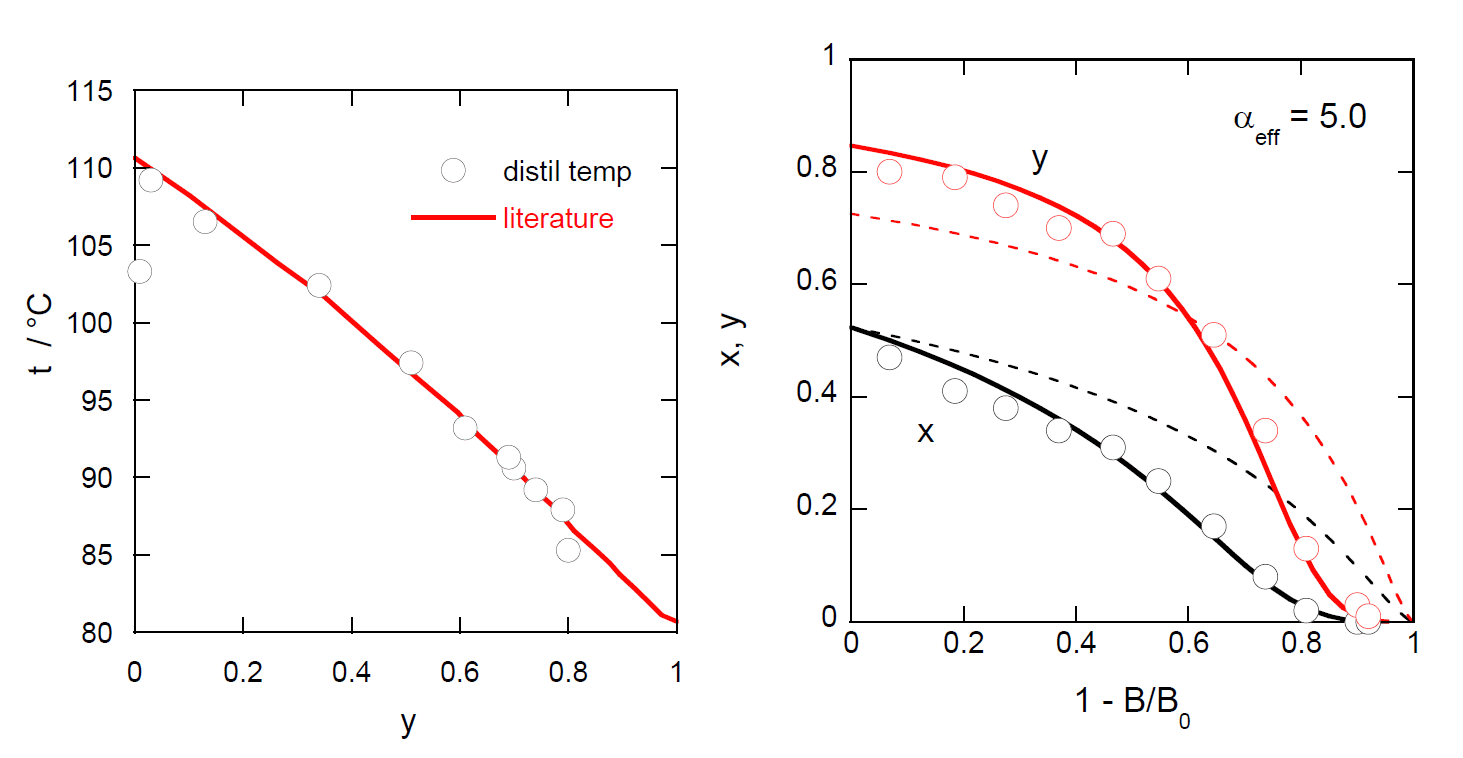
図6-4. 蒸留にともなう(a)留出液組成yと留出温度tの変化と、 (b)混合液体の留出率(1 - B/B0)と留出液組成 y、沸騰液組成xの変化。 (a) 図中の実線は気液平衡の文献値。(b) 図中の実線は実効的な相対揮発度 \(\alpha_{\rm{eff}} = 5.0\) として理想溶液近似を用いたレイリーの式に基づく計算結果。 破線は単蒸留気液平衡から想定される相対揮発度 \(\alpha = 2.4\)を用いた計算結果。
<検討>
- 未回収量がすべて液体の揮散によるものとし、すべての留出分画が同じ割合で揮散したものとして実験結果に補正を加えると、 式 \eqref{eq:m_cumul} に基づくフラスコ中のシクロヘキサン濃度の計算値はどうなるか。
- ト字管の部分を保温せずに外気にさらして蒸気の凝縮を激しくしたら、 実効的な相対揮発度 \(\alpha_{\rm{eff}}\)はどうなるだろうか?
- 精留塔を用いることで、蒸留による分離効率をより上げることができる。 余裕があればウィグリュー管を用いて蒸留を行い、分離効率がどの程度上がるか試してみよ。