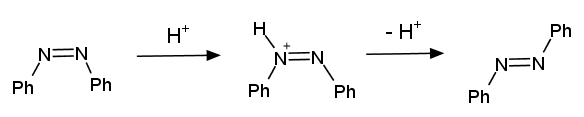
last revised 2020.9 / 2020.5
吉村洋介
6. 相間平衡を利用した物質分離
6-4 クロマトグラフィーによる異性体の分離
<概要>
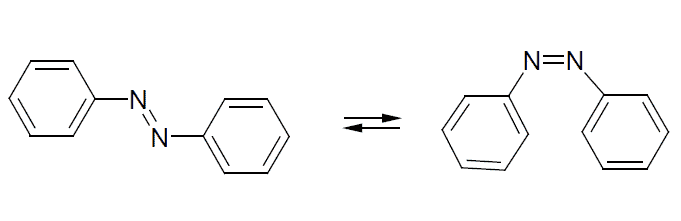
アゾベンゼンはトランス体が安定であるが、光を吸収すると一部シス体への異性化が起きる。
ここではアゾベンゼンの光照射による異性化を、クロマトグラフィーを用いて調べる。
クロマトグラフィーは、移動相(気体のものをガスクロマトグラフィー、液体のものを液体クロマトグラフィーと呼ぶ)を
固定相(通例、微小な粒子からなり、カラムに詰めた状態で使用されることが多い)中に通じることで、
移動相中に含まれる物質の分離・精製を行う。
ちょうど精留において蒸発・凝縮を繰り返すのと同様、カラム中を移動相が通過するとともに注目する物質が、
固定相との間で吸着・脱着を繰り返すことで物質分離が起きることになる。
クロマトグラフィーでは条件を選べば、比較的容易に数千~数万回の吸脱着を繰り返したに相当する分離・精製が可能である
(理論段数と呼ばれるものはこの吸脱着の回数に相当する)。
ここでは手軽に実験室で用いられる薄層クロマトグラフィー(TLC)と、
今日様々な分野で幅広く用いられている高速液体クロマトグラフィーHigh Performance Liquid Chromatography(HPLC)を利用する。
液体クロマトグラフィーを移動相と固定相の極性に注目して、
移動相に極性の低いもの(いわば油)固定相に極性の高いもの(いわば水)を用いる場合を順相normal phase、
逆に移動相に極性の高いもの固定相に低いものを用いる場合を逆相reversed phaseと呼ぶ。
今回TLCでは順相、HPLCでは逆相のクロマトグラフィー行うことになる。
<操作>
- 精密天秤を用いてサンプル管にアゾベンゼン約10 mgをとり、シクロヘキサン約1 mLを加えて溶解し遮光保存する。
- 遮光保存したアゾベンゼン溶液のほぼ半量程度をサンプル管にとって、
紫外線照射装置*1内あるいは蛍光灯下で光照射する(10分程度照射すれば十分である)。
- 遮光したアゾベンゼン溶液と光照射したアゾベンゼン溶液について薄層クロマトグラフィー(TLC)を行う(TLCについては参考資料参照)。
溶離液としてシクロヘキサンを用いた場合とトルエンを用いた場合を比較検討する。
- 精密天秤を用いてサンプル管にアゾベンゼン約1 mgをとり、メタノール約1 mLを加えて溶解し遮光保存する。
- 遮光保存したアゾベンゼン溶液のほぼ半量程度をサンプル管にとって、蛍光灯下あるいは紫外線照射装置内で光照射する(10分程度照射すれば十分である)。
- 遮光したアゾベンゼン溶液と光照射したアゾベンゼン溶液、
それぞれを10 µL 程度とってHPLC装置にかけクロマトグラムを得る(ODSカラム。440 nmで検出。溶離液はメタノール)。
*1
ここで使用する紫外線照射装置はジェルネイル(光硬化樹脂を用いたマニュキュア)用のもので、
日焼けサロン等で用いられているものと同様、紫外部の370 nm付近に大きな強度を持つ。
人体に有害とされる315 nm以下のUVBやUVCといった紫外光はほとんど出ないが、
目に見えない強い光を発していることに注意し裸眼で直視しないようにすること。
<検討>
- TLCとHPLCでのトランス体とシス体の挙動の違いを考察せよ。
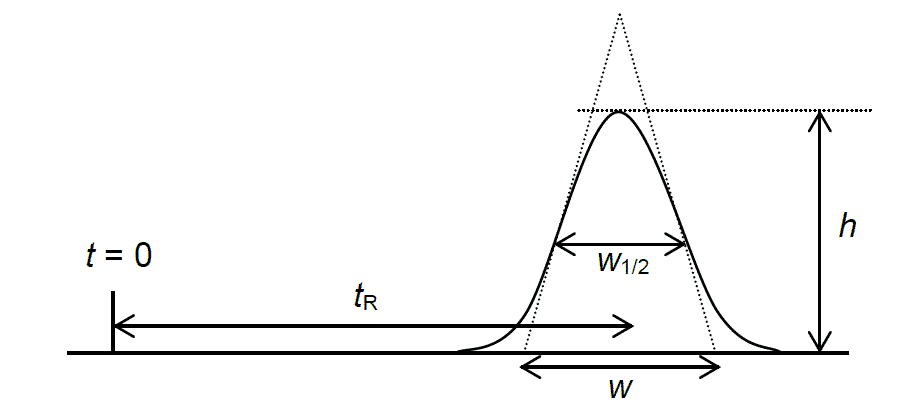
- HPLCのトランス体のピークのデータからカラムの理論段数を評価せよ。理論段数Nは次式で評価できる
\begin{equation}
N = 5.54 \left( \frac{t_R}{w_{1/2}} \right)^2 = 16 \left( \frac{t_R}{w} \right)^2 = 2\pi \left( \frac{h t_R}{A} \right)^2
\label{eq:tpn}
\end{equation}
ここで \(t_R\) は保持時間、\(w_{1/2}\)は半値巾、\(w\) はピーク巾、\(h\) はピークの高さ、\(A\) はピーク面積。
- 式 \eqref{eq:tpn} は理想化された場合に成立する式で、今回の条件設定では保持時間が短いこともあって成立は良くない。
このためトランス体のピークから計算される理論段数の方がシス体のピークから計算される理論段数よりかなり大きく出る。
注入した試料量が有限であるため、移動相と固定相との間の吸脱着によるピークの幅が広がったためにこの相違が生まれたと解釈して、
トランス体とシス体のピークのデータを用いて理論段数を評価してみよ
(試料注入によるピーク幅を \(w_0\) とすると、観測されるピーク幅\(w_a\)は吸脱着によるピーク幅を\(w\)とすると \(w_a^2 = w_0^2 + w^2\)で評価できる)。
- 紫外線照射装置と蛍光灯を用いた時とで、十分長く光照射した後でもシス体の生成する割合は異なる。
照射する光の波長によって、トランス体とシス体の生成比が異なるのはなぜか、
シス体の生成比を大きくするにはどのような波長を選べばよいか考察せよ。
- ここでは溶液を用いているが、固体のアゾベンゼンに光照射してもシス体への異性化が起きてよさそうである。
サンプル管にアゾベンゼンの結晶を少量取って光照射し、光異性化が起きるかどうか調べてみよ。
<参考>アゾベンゼンの幾何異性体の吸収スペクトル
カラムクロマトグラフィーを用いて、アゾベンゼンのトランス体とシス体を分離精製して、
それぞれの吸収スペクトルを測定した結果を図7-8に示す。
トランス体は目に見えない紫外部(400 nm以下)に強い吸収を示すものの、可視部での吸光係数?(吸光係数については資料編II-9参照)はシス体の半分程度である。
今回のHPLCの測定条件では440 nmの吸光度を検出に用いているが、この440 nmでシス体の吸光係数はトランス体の2.4倍程度あり、クロマトグラムの面積比がそのまま物質量の比にならないことに注意する。なお検出に紫外部の320 nm付近の光吸収をとればより高い感度での検出が可能となるが、夾雑物の影響を受けやすくなり、今回の実験では採用していない。
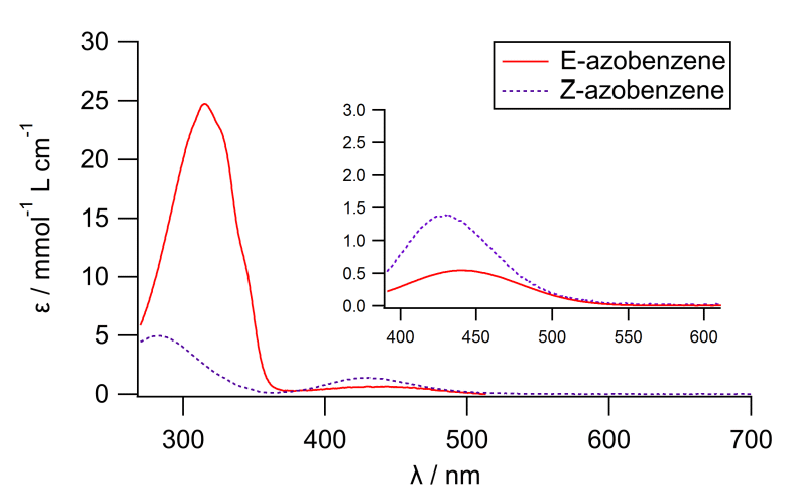
図6-9 アゾベンゼンのトランス体(赤い実線)とシス体(紫の点線)のメタノール中での吸収スペクトル。
挿入図には縦軸を10倍拡大して可視部の吸収を示してある。
クロマトグラフィーによる異性体の分離のこと
高速液体クロマトグラフィー(HPLC = High Performance (Pressure) Liquid Chromatography)は、
今日的には学生時代に触れておくべき分析手法といえるでしょう。
しかし以前選択課題のあった時代、フラーレンの課題(1999-2003年)の中で取り上げられて以降、
まったく触れられることがありませんでした。
そこで2010年に新たな課題を入れる余裕を得た際、何とか割り込ませたのがこの課題になります。
最初に取り上げたのは、ナフタレンのスルホン化の際の異性体分離だったのですが、
分離の際の pH の要件が厳しく、
比較的お手軽なアゾベンゼンの異性体分離を取り上げることになりました。
アゾベンゼンのトランス体とシス体
アゾベンゼンのトランス体とシス体の分離
ざっくりいうと、2相間の分配平衡において、
アゾベンゼンのシス体は双極子モーメントを持ち、トランス体に比して、極性の高い方の相に分配されやすい性質があります。
そのため、
極性の大きい固定相(シリカゲル)を利用する薄層クロマトグラフィー(TLC = Thin Layer Chromatography)では(いわゆる順相 normal phase)、
シス体はトランス体より強く吸着される結果、スポットはトランス体より遅れて上昇し、
極性の小さい固定相(ODS カラム)を利用した HPLC では(いわゆる逆相 reversed phase)、シス体はトランス体より速く流出します。
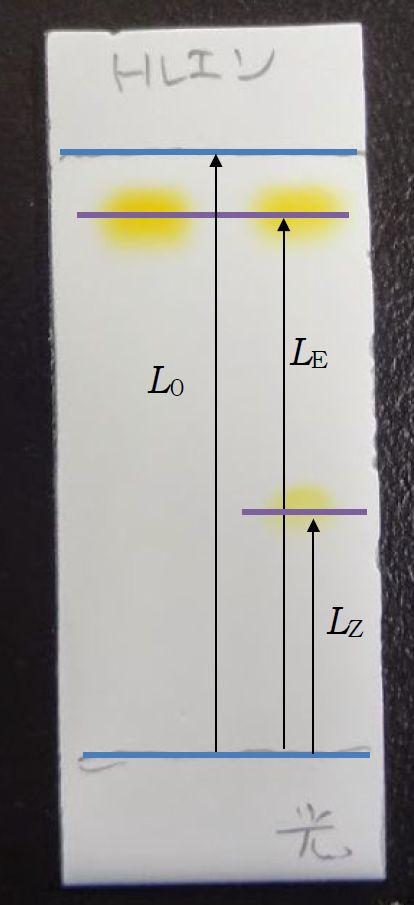
光照射前のアゾベンゼン溶液と光照射後のアゾベンゼン溶液の TLC を取ってみた結果を下図に示します。
光照射することで、生成したシス体による新しいスポットが下方に出現していることが分かります
(ヘキサンで展開した時には原点付近にシス体のスポットがある)。
こうしたスポットの位置を表示するのに、Rf 値が用いられます
(Rf というのは Retardation Factor(遅延係数?) あるいは Retention Factor(保持係数?) の略らしいですが、
どちらが正解かはよくわかりません。
もっぱら Rf と称されています)。
Rf 値は展開液が吸い上げられた先端までの距離とスポットまでの距離の比、
下右図でいうと、トランス体の Rf 値は LE/L0、シス体の Rf 値は LZ/L0 で与えられます。
Rf 値が小さい方が、よりシリカゲルに吸着されやすい物質ということになります。

|
|
|
|
光照射前と光照射後のアゾベンゼン溶液のTLC。
左側の展開液はヘキサン、右側はトルエン。
|
|
Rf 値。
トランス体の Rf 値は LE/L0 = 0.89、
シス体は LZ/L0 = 0.40。
トルエンで展開した場合について示したもの。
|
さてここで光照射前後でアゾベンゼン溶液の HPLC のクロマトグラムがどう変化するかを、
下図に示します。
使用しているのは逆相クロマトグラフィーでよく用いられる ODS カラムで、溶離液はメタノールです
(ODS カラムはシリカの表面を、ODS(= OctaDecylSilyl -SiX2C18H37。X はメチル基だったりいろいろ)基で修飾した充填剤を使用している)。
アゾベンゼンのシス体の方が保持時間(カラムから流出するまでに要する時間)が短く、
TLC の時とは逆に、トランス体より固定相に吸着されにくいことを示しています。
なお通常 HPLC では保持時間が10~20分になるように条件設定するようですが、
ここではお客さん(学生)の回転を速くするため、
リードタイム含め、1 サンプルの分析が5分程度で終わるように条件設定しています。
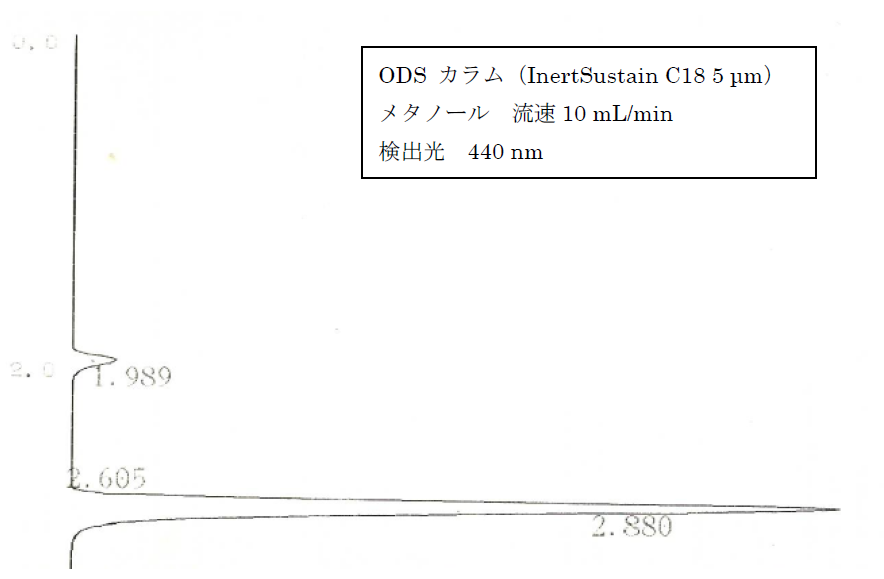
|

|
|
光照射前のアゾベンゼン溶液の HPLC のクロマトグラム。
t = 1.99 min にシス体、
2.88 min にトランス体のピークが現れる。
|
光照射後のアゾベンゼン溶液の HPLC のクロマトグラム。
光照射することで、シス体のピークが大きく成長したことが分かる。
|
アゾベンゼンの光異性化の波長依存性
アゾベンゼンの光異性化に関わって、電子状態の話などいろいろ言い出すと厄介ですが、
大まかには下記のような図式で理解できます。
ここで E はトランス体、Z はシス体で、X* は光励起状態です。
E → X*、Z → X* の単位時間当たりの反応進行度は、
照射光量 Q と E、Z それぞれの光の吸収効率(波長 λ の光を吸って励起状態になる効率)kE(λ)、kZ(λ) に比例します。
そして生成した光励起状態 X* は単位時間当たり、
それぞれ kXE、kXZ の効率で、
トランス体 E、シス体 Z に変化すると考えます。
この図式に基づけば、トランス体、シス体の濃度の時間あたり変化量は次のように表されます。
ジェルネイル用紫外線照射装置の発光スペクトル。
400 nm以下、360 nm 付近に大きな発光ピークがある。
Δ [E] = -kE(λ) Q [E] + kXE [X*]
Δ [Z] = -kZ(λ) Q [Z] + kXZ [X*]
ですから波長 λ の光を当て続け、
トランス体、シス体の濃度変化がもはや起きなくなった状態(光定常状態 photostationary state あるいは photosteady state )になったとすると、
トランス体とシス体の濃度比は次のように表されます。
[Z]/[E] = [kE(λ)/kZ(λ)] [kXZ/kXE]
ですから、光励起状態からのトランス体、シス体の生成効率 kXZ、kXE を一定とすれば、
波長を調整してトランス体の光吸収の効率を大きくしてやれば、シス体の割合が増えることになります。
図6-9 の吸収スペクトルを見ると、
400 nm より短波長側の紫外部ではトランス体の吸収がシス体より大きく、
紫外部の光を照射した方が、シス体の生成に有利です。
今回使用している紫外線照射装置では、もっぱら 360 nm 付近の紫外線を利用していて、
トランス体の吸収極大よりは少し長波長側ですが、
それでも室内灯を照射するよりはシス体が多く生成します。
実際、目視でも、紫外光源を使った方が濃い橙色になっているのが確認できるでしょう。
アゾベンゼンの熱異性化
実験ではアゾベンゼンの光異性化を行わせているわけですが、
生成したシス体は熱的には不安定です。
シクロヘキサン中でもゆっくりトランス体になる反応が進行しますが、
酸で処理すると速やかに安定なトランス体に戻ります。
実際、今回の実験でできた、光異性化したアゾベンゼンのシクロヘキサン溶液に、9 mol/L 硫酸を数滴加えて振り混ぜ、
上澄みのシクロヘキサン溶液の TLC を取ってみると、
シス体のスポットが消失するのがわかります。

|

|
|
アゾベンゼンの光照射後の溶液に 8 mol/L 硫酸を加えたところ。
硫酸塩が生じ、硫酸層が赤褐色になる。
|
硫酸で処理するとシス体のスポットが消える
|
ここではアゾベンゼンの酸型でのシス-トランス熱異性化が速やかに起きることを見たわけですが、
アゾベンゼンの種々の置換体ではこうしたプロトン付加など介さずに、
熱異性化が速やかに起きる例も多く知られています。
たとえばこれまで酸塩基指示薬で登場したメチルオレンジやメチルレッドもアゾベンゼンの置換体ですが、
シス-トランスの熱異性化は極めて速やかに起きます。
また光異性化自体、ほとんど起きないアゾベンゼン類もあります。
こうした異性化の挙動は分子の置かれた環境にも依存し、結晶状態ではアゾベンゼンの光異性化はほとんど起きません
(結晶状態で光異性化の起きるアゾベンゼン誘導体も知られていて、この場合、結晶の変形が起きます)。
理論段数のこと
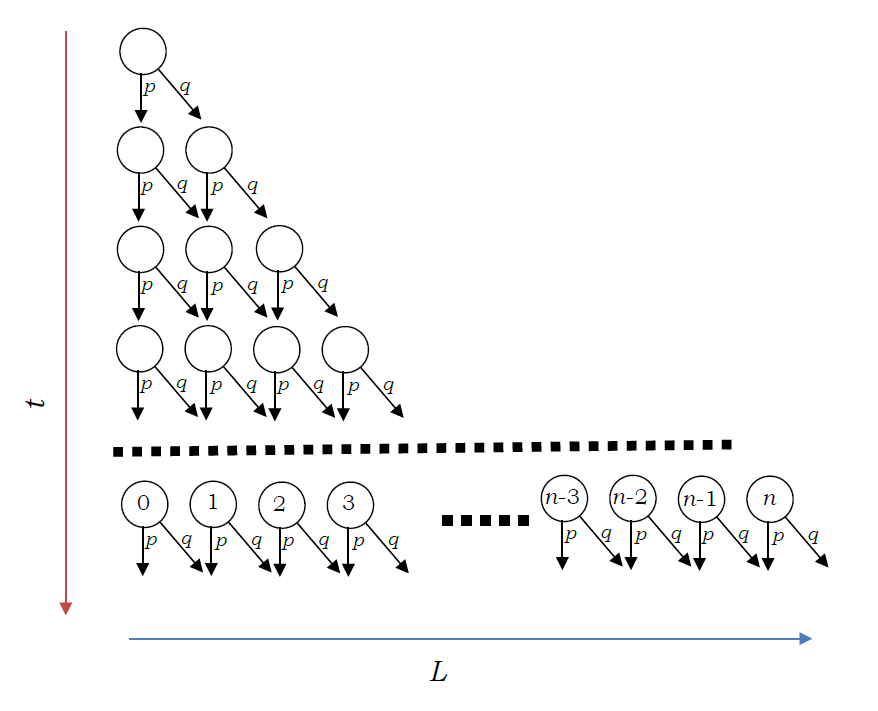
クロマトグラフィーの分離モデル
クロマトグラフィーにおける分離操作を、簡単にモデル化すると右図のようなものになります。
カラムを長さ \(\Delta L\) の多数の区画(段)からなると考え、溶離液が流れることで、
ある時間 \(\Delta t\) 経った後、
区画に存在している物質 X の \(q ~(\ll 1)\) だけが隣の区画に移動し、
後に \(p~ (= 1- q)\) だけ残るとします。
この時、時間 \(n \Delta t\) 経ったときの \(i\) 番目の区画に存在している X の量を \(x(i, n)\) とすると、
次の漸化式が成り立ちます。
\[
x(i, n + 1) = p x(i, n) + q x(i - 1, n)
\]
\(n = 0\) で \(x(0, 0) = 1\)、\(x(k, 0) = 0 ~~ k \ne 0\) とすると、
時間 \(n \Delta t\) 経ったときの、各区画への X の分布は次の2項分布で表されます。
\[
x(i, n) = {}_n {\rm{C}}_i p^{n-i} q^i
\]
区画番号\(i\)(カラム内の位置に相当)の平均は \(nq\)、分散 \(npq\) ですから、
X は \(nq\) 番目の区画の \(\pm \sqrt{npq}\) ぐらいの範囲に分布していることが分かります。
十分 \(n\) が大きければ、時間 \(n \Delta t\) 経った後の X のカラム内の分布は次の正規分布で表されます。
\[
f(i, n) = C \exp \left[ -\frac{(i - nq)^2}{2 npq} \right] \approx C \exp \left[ -\frac{(i - nq)^2}{2 nq} \right]
\]
ここで\(C\) は定数で、最後の関係には \(q \ll 1)\) の条件を用いました。
このモデルによれば、流れとともに X は流され、分布の中心は時間に比例して移動していきますが、
分布の幅は時間の平方根に比例して増えるだけです。
ですから相対的に見れば、分布の幅は時間の平方根に比例して減ることになります。
もし2つの成分が流されているとすれば、
2つの成分の間の距離と、それぞれの成分の分布の幅をとると、
流されれば流されるほど、それぞれの分布は相対的にはより鮮明になり、
差異が際立つわけです。
理論段数の評価
先の分離モデルではどんどん X がカラムの中を流れとともに拡散していく、
ちょうど TLC でスポットの展開を見ている話になっていました。
HPLC の実験ではカラムの長さ L が有限で、
そこから流出してくる X の濃度を時々刻々モニターする形で実験が進行します。
つまり注目するのはカラムの長さ L に相当する分画 \(N = L/\Delta L\) における X の濃度変化です。
この \(N\) を理論段数(number of theoretical plates)と呼びます。
先に見たように \(N\) が大きいほど、相対的に見た分布はより鋭く鮮明になります。
HPLC では理論段数は通常、数千~数万の値になります。
以下では時間と対応すること示すため、\(n\) の代わりに\(\tau\) を用い(\(t = \tau \Delta t\))、
HPLC で得られるシグナルを \(z(\tau)\) とします。
\[
z(\tau) = f(N, \tau) \approx C \exp \left[ -\frac{(N - q \tau)^2}{2 q \tau} \right]
\]
この式は分散が \(\tau\) に依存し、厳密には正規分布の形になっていません。
しかし \(\tau\) の分布が十分狭く、\(\tau = N/q\) 付近でしか値を取らないなら、
上式は次のように書き換えられます。
\[
z(\tau) \approx C \exp \left[ -\frac{(N/q - \tau)^2}{2 \tau/q} \right] \approx C \exp \left[ -\frac{(N/q - \tau)^2}{2 N/q^2} \right]
\]
時々刻々流出してくる X の濃度変化をモニターして、
ピークの位置 \(t_{\rm{R}} = (N/q) \Delta t\)(保持時間)とピークの幅(形状)から標準偏差\(\sigma_t = (\sqrt{N}/q) \Delta t\) を評価したとしましょう。
すると理論段数 \(N\) は次式で評価できます。
\[
N = (t_{\rm{R}}/ \sigma_t)^2
\]
テキストの式\eqref{eq:tpn} はここで示した関係式に基づいて得られています。
ピークの形状が正規分布に従っておれば、式\eqref{eq:tpn} のどの計算を用いても同じ結果になるはずです。
けれども実際のピークの形状は必ずしも正規分布に従わず、必ずしも同じにはなりません。
そもそもこうした計算は、分離過程のモデル化の妥当性に依存していて、
理論段数はその分離カラムの実効的な性能のパラメータと考えるべきでしょう。
相間平衡を利用した物質分離のページへ





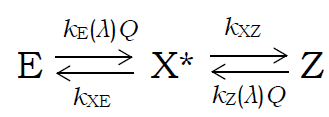
 ジェルネイル用紫外線照射装置の発光スペクトル。
400 nm以下、360 nm 付近に大きな発光ピークがある。
ジェルネイル用紫外線照射装置の発光スペクトル。
400 nm以下、360 nm 付近に大きな発光ピークがある。