2020.10
吉村洋介
反応速度

Ｂ．塩化t-ブチルの加水分解反応

＜概要＞

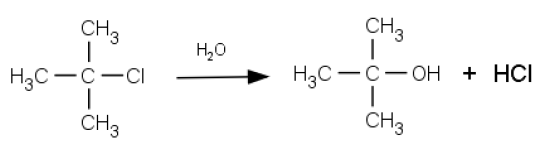
塩化t-ブチルの加水分解反応は求核置換反応のプロトタイプ（SN1）として古くから知られた反応である：

　　　(B)

加水分解の進行とともに塩化水素濃度が増加し、酸塩基滴定や溶液の電気伝導度測定で反応の進行を追うことができる。 ここではこの反応の反応速度を電気伝導度の変化でモニターして速度定数を決定するとともに、 その温度変化から活性化エネルギーを定める。

B-1. 実験操作

  1. メタノールと水を混合して、メタノール50 mass%の溶液を２グループで合わせて250 mL程度調製し各グループで試薬瓶に保存する。
  2. ビーカーに調製したメタノール溶液約40 mLを入れてホットプレートスターラーの上に置き、 スターラーで攪拌しながら天板温度を調節して30～50 °C 程度に保つ （２グループで 5 °C程度刻みに4種類の温度(たとえば30, 35, 40, 45 °C)でのデータがそろうようにする）。
  3. ビーカーに電極を浸し、用意された交流電源（約15 V）に適当な抵抗（20 kΩ 程度）を直列につないで、 下図のような回路を構成し、マルチメーターで電極間の電圧を測る。
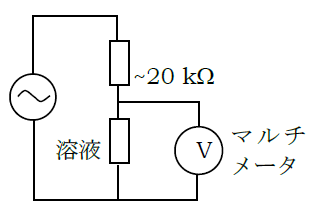
    図5. 溶液の電気伝導度の測定系の概念図。 交流電源に溶液が固定抵抗と直列に結ばれ、 溶液の抵抗変化は溶液にかかる電圧の変化として検知される。
  4. パーソナルコンピュータ（PC）のデータロガープログラムを起動し、 マルチメーターの示度の取り込みを開始する（反応速度に応じておおむね 5～15 s程度おきに 1000回程度まで取り込む設定にしておけばよい）。
  5. 小さいスポイトで塩化t-ブチル 0.05 mL 程度を取ってメタノール溶液に加え、 電圧の変化の様子をPCに取り込んでいく。
  6. 温度を変え同様に電気伝導度変化を測定する。
  7. 【余裕があれば】溶液に水を加え、メタノール濃度下げて加溶媒分解速度を測定せよ。

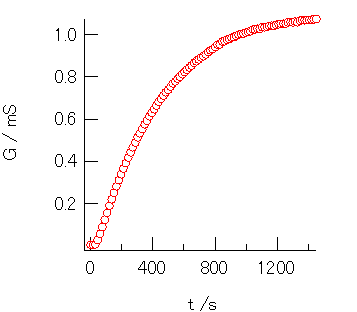
図6. 塩化t-ブチル添加後の50 %メタノール水溶液の 電気伝導度の時間変化の実験例（31 °C）。

B-2. 結果の解析

電解質溶液の電気伝導度 \(G\)（S cm-1 単位で表されることが多い）は、概ね、 溶存しているイオン種の濃度と比例関係にあるとみなせる。したがって塩化t-ブチルの加水分解反応

\begin{equation} \mrm{BuCl + H_2 O \rightarrow BuOH + HCl} \label{eq:BuCl_hydrolysis} \end{equation}

において、溶液の電気伝導度 \(G\) は関係する分子種の中で唯一電解質である塩化水素濃度[HCl]に比例すると考えられる：

\begin{equation} G = a \mrm{[HCl]} \label{eq:cond} \end{equation}

時刻 \(t = 0\) での塩化t-ブチル濃度を [BuCl]0、塩化水素濃度を[HCl]0としよう。 加水分解の反応速度が塩化t-ブチル濃度に対し１次の速度則に従うものとすると次の微分方程式が成り立つ：

\begin{equation} -\frac{\rmd \mrm{[BuCl]}}{\rmd t} = \frac{\rmd \mrm{[HCl]}}{\rmd t} = k \mrm{[BuCl]} \label{eq:BuClrate} \end{equation}

この微分方程式から塩化水素濃度について次式が得られる：

\begin{equation} \mrm{[HCl] = [HCl]_0 + [BuCl]_0} (1 - \mrm{e}^{-kt}) \label{eq:HClconc} \end{equation}

溶液の電気伝導度は塩化水素濃度に比例するとみなせる（\eqref{eq:cond} 式）ので、 電気伝導度の時間変化は次式のような指数関数で表されることになる：

\begin{equation} G = (G_0 + C) - C \mrm{e}^{-kt} \label{eq:cond_change} \end{equation}

ここで \(G_0\) は時刻 \(t = 0\) での電気伝導度であり、\(C\) は \(a \mrm{[BuCl]_0}\) である。 こうして課題Aで吸光度変化を取り扱ったのと同様にして、電気伝導度変化から速度定数を得ることができる。

一般に反応速度定数kは熱力学温度 \(T\) を高くすると大きくなり、 その温度依存性は次のアレニウス Arrhenius の式でおおむね表現することができることが知られている：

\begin{equation} k = A \mrm{e}^{-E_\mrm{a}/RT} \label{eq:arrhenius} \end{equation}

ここで \(R\) は気体定数であり、\(E_\mrm{a}\) は活性化エネルギー、 \(A\) は前指数因子と呼ばれる反応のパラメータである。 速度定数 \(k\) の対数を温度の逆数 \(1/T\) に対してプロットすると （このプロットをアレニウスプロットと呼ぶ）直線関係が得られ、 直線の勾配から活性化エネルギーが、切片から前指数因子が得られることになる。

B-3. 検討課題

  1. IGOR Proを用いて電気伝導度の時間変化が exp_XOffset関数（y0 + A exp(x/τ)。xのオフセットを0に固定）に当てはめることができることを確認し、 加水分解速度定数を決定せよ。
  2. 異なる温度における２グループの速度定数のデータを用いて、 速度定数 \(k\) の対数を温度の逆数 \(1/T\) に対してプロットし、活性化エネルギーを求めよ。
  3. 求核置換反応SN1の反応機構から、 水を加え溶媒の極性を大きくしたときの反応速度についてどのような解釈ができるか。
  4. 最初に 1.0 mol/L 水酸化ナトリウム溶液を 0.5 mL程度加えてから、 塩化t-ブチルを同様に添加して電気伝導度変化を測定するとどのような結果が得られると予想されるか？ また実際に確かめてみよ。

反応速度のページへ