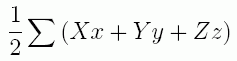(2.1.1)
多数の質点が互いに相互作用しながら、容器の中で乱雑に運動しているものとします。 こうした系について、クラウジウスが当初述べた古典的なビリアル定理は次のようなものでした：
系の平均活力は、その（平均）ビリアル（の大きさ）に等しい。
ここで登場する「活力」（"vis viva"）は、今日の運動エネルギーに相当します。 そもそも「活力」は古典力学の草創期にライプニッツが導入した量で、 今日の運動エネルギーの２倍に相当する量 mv2ですが、 クラウジウスは (mv2)/2、ちょうど運動エネルギーと同じ量として用いています。 そして定理の名前にも出てくる「ビリアル」はクラウジウスが導入した量で、 クラウジウスは次のように定義しました （以下、記号なども特に記す以外は、クラウジウスの原論文に忠実に再現してみます）。
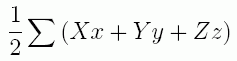(2.1.1)
ここで X は質点に働く力の x 方向成分、Y は y 方向成分、Z は z 方向成分です。
上のビリアル定理を式の形で書くと次のようになります：
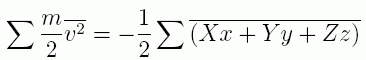(2.1.2)
ここで m は質点の質量、v は速度、上部に線を引いた記号は平均をとったことを意味します。
クラウジウスはこの関係式を、座標の２乗の時間微分から次のようにして導きました。
x 座標の２乗の２階の時間微分は次のように、x 座標の１階の時間微分（速度）の２乗と、x の２階の時間微分（加速度）と x の積の和で表わされます。
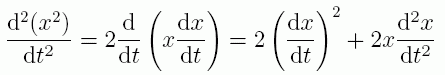(2.1.3)
この式から次式を得ます：
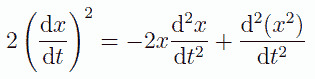(2.1.4)
力の x 方向成分 X は、加速度 d2x/d t2 に質量 m をかけたものですから、
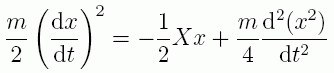(2.1.5)
ここで上式の時間平均を取ってみます。
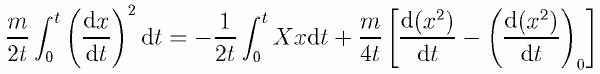(2.1.6)
ここで (d (x2)/d t)0 は、 (d (x2)/d t) の初期値を表わします。 左辺と右辺の第１項の積分は時間が立つにつれて増加していく量で、 それを時間 t で割ったものは、時間 t を十分長く取ればそれぞれの平均値になります。 右辺第２項は、もし周期運動なら時間 t が周期に等しければ0です （マクスウェルはビリアル定理の成り立つ例として等速円運動を挙げています。 求心力の表現 F = -mv2/r からただちに、mv2 = -Fr が得られます）。 周期運動でなくとも十分時間を長く取れば、 時間が長くなるにつれて無視できる大きさになってしまう量です。 したがって平均を取ると右辺第２項は消え、ビリアル定理が得られます。
クラウジウスの貢献は、上のビリアル定理を導いたに止まりません。 クラウジウスはビリアルに対する、質点間の相互作用による寄与（内部ビリアル）と 外力による寄与（外部ビリアル）との存在を見通しました。
距離 r 離れた２つの質点間に中心力 -φ(r) が働くものとすると（符号が逆になっていることに注意）、 この２つの質点についてビリアルを計算すると次のようになります（作用・反作用の法則に注意）：
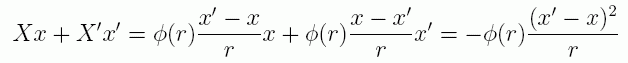(2.1.7)
ですからビリアルは、対間の分子間力を用いて次のように表現できます：
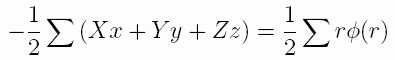(2.1.8)
ここで左辺の総和はすべての質点について、右辺の総和はすべての質点の対についてとります。
上の取扱いでは分子間力からの寄与（内部ビリアル）を考えたわけですが、 外力が働いている場合にはそれも考慮しないといけません。 クラウジウスは特に容器の中の流体、 体積 V の系に圧力 P が及ぼされている場合を考えました。 この場合、外力によるビリアルへの寄与（外部ビリアル）は (3/2)PV となります （クラウジウスは圧力・体積に小文字を使っていますが、運動量・速度と紛らわしいので大文字で表記します）。 クラウジウスは外部ビリアルについて結果を示しているだけで、 導出は示していませんが、 ファンデルワールスに倣って念のため記しておくと次のようになります：
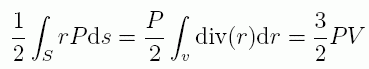(2.1.9)
ここで表面積分を体積積分に置き換えるのに、 ガウス（オストログラツキー）の公式を使いました（div(r) = ∂x/∂x + ∂y/∂y + ∂z/∂z = 3）。 あるいはもっと単純に、一辺の長さ L の立方体を考え、 座標原点をその一頂点に置くと、原点を含まない３つの面にそれぞれ働く力 P L2 に、 原点から面までの距離 L をかけて 2 で割って、(3/2)PL3 = (3/2)PV という結果を得ます。
こうしてクラウジウスは、質点の内部運動の活力 h（運動エネルギー。彼はこれを熱と呼んでいます） に対する次のような表式を与えました：
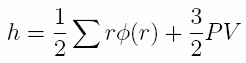(2.1.10)
これが今日、ビリアル状態方程式といわれるものの原型ということになります（再度φ(r)が分子間力の符号を逆にしたものであることを強調しておきます）。
今日の目から見るとちょっと意外ですが、 マクスウェルの速度則が液体に対して適用可能かどうかについて、 1870年当時の科学者たちには、マクスウェルその人も含めて、ためらいがあったようです （補記参照）。 ですからクラウジウスは、前節で見たビリアル状態方程式にあと一歩というところに来て、 状態方程式（圧力-体積-温度の関係）には届きませんでした。 この一歩を踏み出したのは、ファンデルワールスであったと思われます。
マクスウェルの速度則は1859年に発表され（刊行されたのは1860年）、ある方向の速度成分を取り出すと次のような形を取ります。
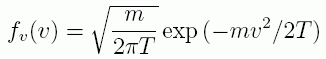(2.2.1)
ここで簡単のため、絶対温度にボルツマン定数をかけたものを、温度 T としました。 これは温度の次元をエネルギーに、単位をボルツマン定数にとったことになります。 本稿では温度に対し、以降もこの記法を用います。 このマクスウェルの速度則のポイントは、 分子の速度分布が流体の密度に依存していないことです。 つまり流体をいくら圧縮しても、温度が同じなら分子の並進速度の分布には変化がなく、 平均の並進運動エネルギーは、x、y、z それぞれの方向成分について T/2 になります。 この平均並進運動エネルギーと温度の関係をそのまま適用すれば次式を得ます （今日通用の表記と合わせるように、分子間力の表記としてf(r) = -φ(r)を用いました。 また平均を ＜・・・・＞ で表記するようにします）。
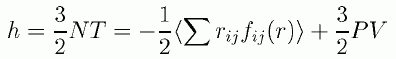(2.2.2)
これを整理して、次のような形の式を通常、ビリアル状態方程式と呼びます。
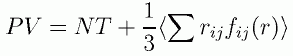(2.2.3)
同じ式ですが圧縮率因子 PV/NT の形で整理することもよく行われます。
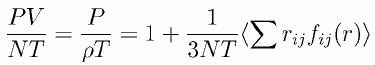(2.2.4)
教科書にしばしば登場するビリアル係数は、 この右辺第2項を密度で展開した時の係数に相当します。
クラウジウスのビリアル定理は、 容器の中が平衡状態にあることを前提としているだけですから、 水とアルコールの混合系でも（あるいは水と水蒸気といった不均一系でも）成り立ちます。 ここでは異種粒子の混合系について、 留意すべき事項をひとつ挙げておきましょう。
ビリアル定理を系全体のビリアルではなく、１個の分子について考えてみます。 １個の分子についても、次式のビリアル定理は成立します。
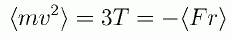(2.3.1)
するとたとえば、水とアルコールの混合系では、 水かアルコールかどちらかの分子にだけ注目して内部ビリアルを求めれば、 それで系全体の圧力を知ることができるように思われるかもしれません。 しかし事態はそんなに単純ではないのです。
問題は外部ビリアルにあります。 １個の分子に及ぼされる外部ビリアルの評価は単純ではありません。 まったく同じ分子からなっておれば、 単位面積の器壁から１個の分子が受ける力は、 圧力を全体の粒子数で割ればよいでしょう。 しかし異なる分子の混合物であると、 器壁から受けた力を成分に分配する簡単な方法はありません。 器壁からある分子に及ぼされる圧力を知るには、 その分子についての内部ビリアルを計算して割り出すことになります。 ですから系全体の圧力を知るには、 結局のところ、それぞれの成分分子１個あたりの内部ビリアルを知る必要があるのです。
古典的なビリアル定理は前節で見たように、 分子に働く力と運動エネルギーの間の関係を扱うものでした。 この関係をもっと一般的な観点から扱うために、運動量と座標の関数 Y(p,q) を考え、 Y(p,q) が定常的に振舞うとします。 すると定常的なわけですから Y(p,q) の時間微分は0で、次の関係が成り立ちます。
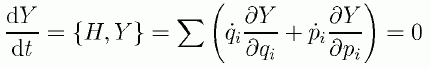(2.4.1)
ここでは解析力学の記法にならってポアソン括弧を使って書いてみましたが（H はハミルトニアン）、 多変数関数の微分をあからさまに書いてみただけのことです。
ここでY(p,q) として運動量と座標の積 pq を取れば、 以下のようにクラウジウスのビリアル定理をえます。
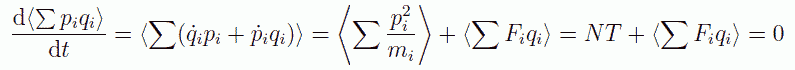(2.4.2)
さて Y(p,q) として今度は運動量と力の積 pF をとると、次の関係式が得られます （ここでは話を簡単にするため、ある１個の粒子 i について考えます。 また pi、qi、Fi などは、 粒子 i に関する運動量、座標、力に関する、ある方向の成分を示すものとします）。
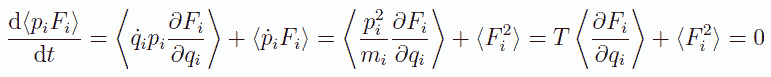(2.4.3)
ここで力 Fはポテンシャルエネルギー U を座標で微分したものですから、 次のようなポテンシャルエネルギーの２階の微分と１階の微分の間の関係式の形に整理できます。
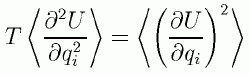(2.4.4)
粒子がかりにある地点にバネで結ばれているとすると、 そのバネ定数が大きいほど粒子には大きな力が働くことになるわけです。 この関係式は古典統計力学に対する量子補正、 あるいは力の相関関数の評価などで登場するので出会われた方も多いかと思います。
ここではこれ以上触れませんが、 関数 Y(p,q) に種々の物理量を設定してえられる関係式一般を「超ビリアル定理」 hypervirial theorems と呼びます。
ぼくは１８７０年当時の事情について、マクスウェルの論文や本（Theory of Heat）、 ファンデルワールスの学位論文などで推測していただけですか、 最近この件に関わって J. S. Rowlinson による興味深い論文が発表されました（Mol. Phys. の Widom 記念号）。
J. S. Rowlinson, Mol. Phys. 103, 2821 (2005): "The Maxwell-Boltzmann distribution"
ボルツマンの長大な論文に辟易したか、 マクスウェルが液体等へのマクスウェルの速度則の適用に懐疑的であったことなど、 マクスウェルの速度則の凝縮系への適用をめぐる さまざまな動向が紹介されていて興味深いです。 １８７０年代当時、そしてそれ以降もマクスウェルの速度則の凝縮系への適用の可否は大きな問題で、 マクスウェルは 「もし本当なら、分子科学においてもっとも重要な原理 （the most important doctrine, if true, in molecular science）」 とコメントしたとのこと(1878年)です。
なおクラウジウスは、すでに1862年に マクスウェルの速度則が液体でも成立することを強く主張していた (R. Clausius, Ann. Phys. 116, 73 (1862). see 95) 由ですが、 なぜ1870年のビリアル定理の論文で、それを主張しなかった（形にしなかった）のかは、 この論文を見ても？？でした。