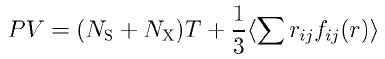４．ビリアル定理からみた圧力の諸相

４．１．溶媒と相互作用しない溶質分子

溶液中の相互作用というと「溶媒-溶媒」「溶媒-溶質」「溶質-溶質」という組み合わせで尽くされたように、 普通考えられているようです。 クラウジウスのビリアル定理は、 ここに忘れられたもう一つの要素、 「器壁との相互作用」があることを外部ビリアルの形で示しています。 このことを明瞭に示す例として、溶媒と相互作用しない溶質分子の熱力学的性質を考えて見ましょう。

純粋な溶媒Sに、溶媒分子と相互作用しない溶質分子Xを1個だけ、体積一定の条件下で投入したとしましょう。 このSとXの混合系のビリアル状態方程式は、次のような形になっています。

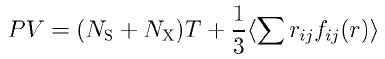　　(4.1.1)

ここで内部ビリアルの項は、溶媒-溶媒の相互作用だけで決まっていて、溶質Xが1分子加わっても何の変化もおきません。 ですから溶質分子を1個入れたことにともなう圧力変化は、次式のとおり理想気体の状態方程式から得られるものと同じです。

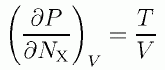　　(4.1.2)

溶媒分子と相互作用しない溶質分子による圧力の増加は、 溶媒の個性によらず一定の値になるわけですが、 「体積の変化」に目を転じるとことは単純ではありません。 圧力一定の条件下でXを加えたときの体積変化（部分分子容）を評価すると次のようになります。

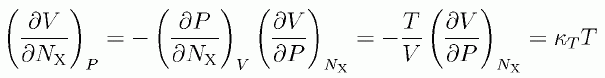　　(4.1.3)

ここで κ_T は溶媒の等温圧縮率です。 溶質分子Xの投入にともなう圧力の増加が溶媒の個性（等温圧縮率）を通して、 体積の変化として観測されるというしかけになっているわけです。 このように注目する量によって、壁との相互作用の現れ方が違ってくることには注意が必要です。

４．２．剛体壁近傍の分子の密度と圧力

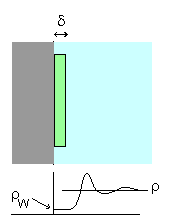
剛体壁付近の分子の分布。 壁の極近傍の厚みδ、断面積 S のセンベイ状の領域に関するビリアル定理を考える。 　かりに室温付近で１気圧の液体であれば、剛体壁近傍の数密度ρW は、１気圧の空気の数密度と同じで約 0.04 mol/L になる。

剛体的な壁で仕切られた容器の中に粒子が閉じ込められているとしましょう。 また問題を簡単にするために、粒子は球形であるものとします。 容器の壁近くの、断面積 S で非常に薄い厚みδの領域を考えます。 この領域には、圧力 P が働いているので、ビリアルとしては 3PS δです。 領域内の粒子間の相互作用の寄与は、厚みδを十分薄くとれば無視できます。 （内部ビリアルの寄与は、粒子数に1個の粒子の周りの粒子数に比例すると考えられます。 粒子数、粒子の周りの個数、ともに厚みδに比例するので、 内部ビリアルはδの２乗のオーダーになります。） ですからこの薄いセンベイ状の領域にビリアル定理を適用すると次式が成立することになります（N_Wは剛体壁近傍の薄いセンベイ状の領域中の粒子数、Vはセンベイ状の領域の体積。 ρ_Wはその密度です）：

　　(4.2.1)

　　(4.2.2)

つまり理想気体の状態方程式が成り立つのです （分子運動論からも同じ結果が得られます）。

現実の液体はさまざまな圧縮・膨張挙動を示すのに、 液体によらず上式が成り立つのは一見不思議に思われるかもしれません。 種々の液体の個性は、この式中の剛体壁近傍の粒子密度に反映されているのです。 この意味では、分子間相互作用から状態方程式を予測する作業は、 広く平らな剛体壁近傍の粒子密度を推定する作業でもあるわけです。 あるいは同じ温度圧力の液体を比較するという操作は、 剛体壁との接触面における液体の数密度が等しい条件で、 液体を比較していることに相当するわけです。

同様のことは、剛体壁がもっと分子論的なものであっても成立します。 このことを利用して剛体球からできた流体の状態方程式を考えて見ましょう。 簡単のため剛体球の直径を1とします。

剛体球表面にかかる平均の圧力を P_C = ρ_C T とすると、 1 個の分子に注目した時の内部ビリアルの値は次式で与えられます。

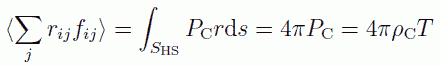　　(4.2.3)

ビリアル状態方程式の中の内部ビリアルは、 すべての分子対の間に働く力のビリアルを問題にしています。 上の分子1個に注目した内部ビリアルを単純に粒子数 N 倍すると、 １対の相互作用を２重に勘定したことになります。 このことに注意して、剛体球流体の内部ビリアルは、 剛体球表面の剛体球密度 ρ_C を用いて次のように与えられます。

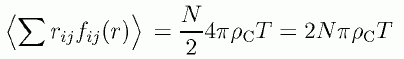　　(4.2.4)

ビリアル状態方程式にこれを代入し、最終的に次の表式が得られます。

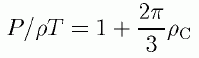　　(4.2.5)

十分剛体球流体の密度が低ければ、剛体球表面の密度は全体を均した密度ρに等しいと考えられます。 上式の第2項の係数が、第2ビリアル係数に等しくなっていることは、すぐにおわかりでしょう。

このように剛体壁近傍の密度 ρ_W 、剛体球表面の剛体球密度 ρ_C 、 それぞれと圧力を関係付ける式が得られたわけですが、 最後に ρ_W と ρ_C の関係を整理しておきましょう。 上記の式から ρ_W と ρ_C の間には次の関係が成り立ちます。

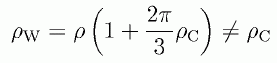　　(4.2.6)

剛体壁近傍の密度は、剛体球表面の剛体球密度と異なります。 このことは外圧がそのままの形で、 分子表面に働くものではないということを示している点で重要です。 あるいは流体力学のパスカルの原理は、 分子レベルでは一般に成立しないともいえるでしょう。

この節の最後に、 外圧と分子表面に働く圧力が一致するきわめて例外的な例として、 １次元の剛体棒系があることを挙げておきましょう。 剛体棒同士の接触距離の密度は、剛体壁と剛体棒の間の接触距離の密度と同じですから、 次の式が成り立ちます。

　　(4.2.7)

１次元では内部ビリアルの前の係数は３次元と異なり1になることに注意ください （ div (r) = 1で、また排除体積の大きさが2になっている）。 ですからここから直ちに、次の１次元の剛体棒流体の状態方程式を導くことができます （Korteweg-Tonks の式）。

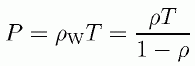　　(4.2.8)