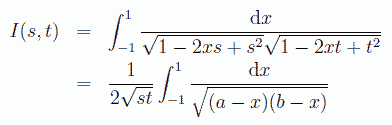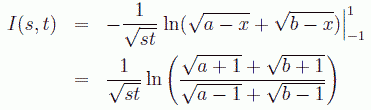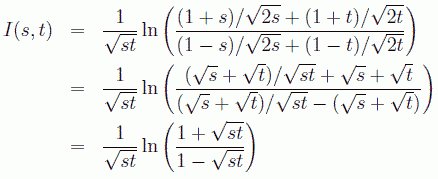(5.1.1)
１９世紀には分子間の相互作用と巨視的な物性を結ぶ関係式として、 大きな存在感を持ったビリアル定理ですが、 今日の統計力学の教科書では状態和（分配関数）が圧倒的な地位を占めていて、 ビリアル定理にはほとんど日が当たりません。 今日の統計力学の基礎を作ったGibbs の著書にも、ビリアル定理は見当たりません。 この事情について考えてみます。
ビリアル定理が日の目を見ないことにはいくつか理由があるでしょうが、 まずビリアル定理それ自身が、 熱平衡に向かう変化の方向に関して、あまりよい見通しを与えないことが挙げられるでしょう。
等温過程について状態和の立場からは、 「カノニカルな状態和が大きくなる方向に系は変化する」 と、明確な形で主張できます。 ビリアル定理では、 「「ビリアルの大きさが平均運動エネルギーの２倍と等しくないなら、 系は平衡にない」と主張することはできます。 でもそれからさらに進んだ議論は困難です。 そもそも分子に働く拘束力が大きいなど、量子力学的な効果が重要になってくると、 平均運動エネルギーを (3/2)NT で評価できなくなり、 熱力学量との対応がつけづらくなってしまいます。
この一方、状態和は温度をパラメーターとする、 エネルギーのモーメント母関数です。
(5.1.1)
ですから種々の物理量が、 状態和に対する簡単な微分操作で与えられるというメリットがあり、 それに対応する熱力学関係式が容易に構成できます。 たとえばエネルギーについてはすぐに次のような関係が導けます。
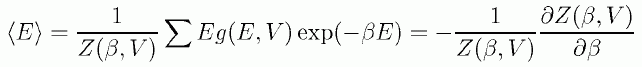(5.1.2)
そして状態和とヘルムホルツの自由エネルギーの関係を用いれば、 この関係式がギブズ-ヘルムホルツの関係式であることが直ちに分かります。
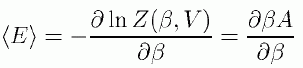(5.1.3)
このように熱力学の体系との整合性を考えたとき、 ビリアル定理からする立論は不利な立場に立たされます （Gibbs の本 [G02] の題名に"... developed with especial reference to the rational foundation of thermodynamics" とあることは示唆的です）。 こうしたことから「状態和さえわかれば、何でも分かる！」という主張も生まれます。 いわば「状態和教」のドグマとでもいえましょうか。
状態和の方法は強力な方法であるのですが、 実際に分子間力と種々の熱力学量を橋渡しするのには、 必ずしも適さないということは注意されてよいことだと思います。 圧力についての表式を見てみると、この事情が見えてきます。 すなおに状態和から、圧力の表式を導出すれば、次のような式が得られます。
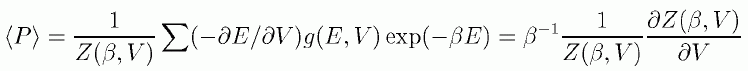(5.2.1)
この式は熱力学的には、ヘルムホルツの自由エネルギーの体積微分が圧力を与えるというのと同じことです。
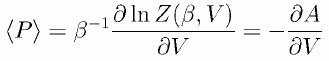(5.2.2)
ここまではいいのですが、 上式中の断熱的な条件下でのエネルギーの体積微分 - ∂ E/∂ V を、 分子間相互作用から与えることは困難です。 そして液体論の教科書類では、状態和からビリアル定理を導くため、 体積に依存するポテンシャルを導入する手法（戸田-Born-Green）がよく登場し、 ビリアル定理が導出されています。
状態和を用いてビリアル定理を証明する試みは、「導出」あるいは「検証」ではあっても、 「証明」と呼ぶには足りないというべきでしょう。 なぜなら熱力学的な平衡状態（あるいは単に定常状態）の存在、 外力と分子間相互作用の寄与の区分が、ビリアル定理を成立させているからです。 けれどもビリアル定理を状態和から導出しないと、 ビリアル定理それ自身がいかがわしい目で見られかねない空気があることも確かです。 ぼくにはそれが「状態和教」、 何でも状態和の支配下に置かないと気がすまない、 どこか偏執狂的な情念のなせる業のように思えます。
状態和の方法あるいは母関数の方法は、強力で有効なのですが、 すべてを母関数に帰着させようとすると、 かえって事態の見通しを失わせてしまうことは、 もっと認識されてよいように思います。
例としてルジャンドルの多項式 Pn(x) における母関数の方法を見てみましょう。 ルジャンドルの多項式の母関数は次のように構成できます。
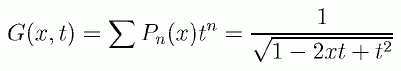(5.3.1)
これを x について微分すると、次の関係式をえます。
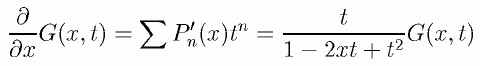(5.3.2)
この恒等式を t のべきについて整理して、係数を比較することで次の関係式が導出できます。
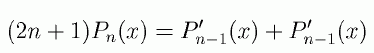(5.3.3)
同様にしてさまざまなルジャンドル多項式の関係式が導出されます。 こうした関係式の導出に当たって、母関数の方法はまさに鬼神のような働きをします。
ところでルジャンドル多項式を考える上で、 もっとも基本的な性質と思われる直交性についてはどうでしょうか？ 次式のように異なるパラメーター s, t を持つ母関数の積について内積を考えます。
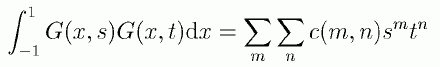(5.3.4)
この内積の展開の係数 c(m, n) が、 m=n でないかぎり0になる、 つまりこの積分は st の関数として記述できるはずです。 実際に上式の計算を実行してみると次のようになり、 直交性が成り立っていることがわかります。
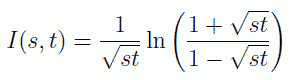(5.3.5)
たしかに母関数の方法で直交性は示せました。 しかしこの計算の向こうにあるルジャンドル関数の風景・構造は、 どんなものだったのでしょう？ 少なくともぼくには、ルジャンドル関数の特性といったものをそこから見出すことができません。
母関数の方法を取るよりは、 もとのルジャンドルの多項式がルジャンドルの微分方程式
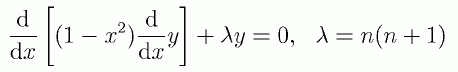(5.3.6)
の解であることに注目した方が、 ぼくは、はるかに手ごたえの確かな実質を手にした気がします （異なる固有値に属する固有関数は直交する）。
母関数の方法に立つなら、いわば計算だけしておればよいようなものです。 でもその計算の向こう側をうかがい知るには、 きわめて豊かな想像力を要するように思われます。 何も母関数にしがみつく必要はないはずです。 一度、母関数の方法から離れたところから始めることで、 もっと多くの彩りにとんだ世界に到ることができるのではないかと、 ぼくは密かに期待しています。
