|
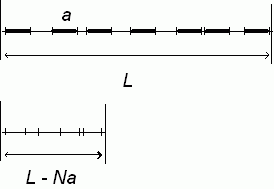
図 4-1. 剛体棒のサイズを縮めて質点にする。
系の長さは L - Na になり、元の系での剛体棒間の長さは (m + 1)a (m は元の系で中間に存在した剛体棒の本数)だけ短くなる。 |
Zernike と Prins は、1次元剛体棒流体の動径分布関数を、 ポアソン過程で見たのと類似の方法で導出しました (彼らは気体中の分子の自由行程の取扱いとのアナロジーを挙げています)。 ここでは Zernike と Prins の論文の表式を今日的な表式に直して、 1次元剛体棒流体の動径分布関数を導出してみましょう。
1次元剛体棒流体で、分子の中心の位置の間の相関を考えます。 ある分子からの距離が x と x + dx の間に分子を見出す確率を ρg(x) とします。 まったくでたらめに配置しているとすれば(たとえ分子同士が重なろうと無理やり配置したと考えます)、 g(x) = 1 です。 また g(x) = g(-x) です。
Zernike-Prins は、ρg(x) を単に g(x) と置いていますが(これは Ornstein-Zernike でも同じ)、 ここでは今日の動径分布関数の定義に即して ρg(x) と表記します。
あきらかに x < a に対しては g(x) = 0です。 また a < x < 2a であれば、注目する分子間に他の分子は存在できません。 一般に na < x < (n+1)a なら、間に介在する分子数はたかだか n - 1 個です。 ここで、ある分子から数えて n 番目の分子が距離 x と x + dx の間に存在する確率、 ρg(n)(x) を考えることにします。
剛体棒分子の配置の問題は、先のポアソン過程とよく似ているのですが、 剛体棒分子に大きさがある点を考慮しなければなりません。 剛体棒分子のコアの長さ a を小さくしていって 0 にまでしたとしましょう。 すると剛体棒分子の配置の問題は、長さ L - Na の線上の点の分布の問題に置き換えられたことになっています。

|
図 4-1. 剛体棒のサイズを縮めて質点にする。
系の長さは L - Na になり、元の系での剛体棒間の長さは (m + 1)a (m は元の系で中間に存在した剛体棒の本数)だけ短くなる。 |
この圧縮された剛体棒流体の描像での注意点の第1は、 この線上での質点間の距離 x' と、元の剛体棒流体における距離 x との対応が、x' の間に存在する質点の数に依存していることです。 かりに x' の距離の間に m 個の質点があれば、もとの剛体棒流体での距離は x' + (m + 1)a です。 2点目は質点の平均密度が、剛体棒の密度 N/L より高くなって、N/(L - Na) になっていることです。 また質点の最近接距離の平均値 lv は剛体棒の最近接距離の平均 L/N より a だけ短くなります。
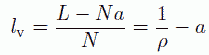 (4.1)
(4.1)
上記のことに注意して、剛体棒分子の間の動径分布関数を求めると、 まず最近接の剛体棒同士については次のようになります。
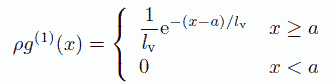 (4.2)
(4.2)
同様にして一般に第 n 近接の剛体棒分子間の動径分布関数は、 次の式で評価されます。
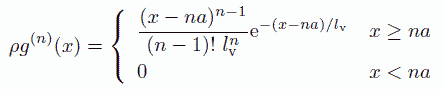 (4.3)
(4.3)
そして最終的に剛体棒流体の動径分布関数は、これら第 n 近接の分布関数の和で表現されます。
ρg(x) = ρ Σ g(n)(x) (4.4)