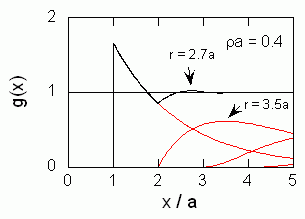
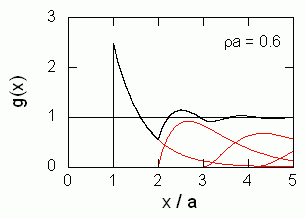
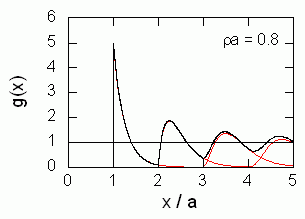
図 5-1. 種々の密度における1次元剛体棒流体の動径分布関数。 図中赤い実線は、それぞれ第1近接、第2近接、第3近接、第4近接の分布関数に対応する。
ここでは少し、1次元剛体棒流体の動径分布関数から見えることについて触れましょう。



図 5-1. 種々の密度における1次元剛体棒流体の動径分布関数。
図中赤い実線は、それぞれ第1近接、第2近接、第3近接、第4近接の分布関数に対応する。
先の動径分布関数についての表式から計算される、動径分布関数を図に示しました。 動径分布関数に現われるピークからから、従来「第1溶媒和圏」「第2溶媒和圏」「第3溶媒和圏」・・・ と分類されてきたものが、必ずしも第1近接分子、第2近接分子、第3近接分子、・・・に対応しないことが分かります。 このことは特に密度を下げていくと顕著です。
剛体棒流体において、第 m 近接分子の分布のピークは a + (m - 1)/ρ です。 また第 m 近接分子までの平均距離は一般に m/ρ になります。 これらの総和として眺めた動径分布関数のピークの位置は、それが m 番目のピークだからといって、 必ずしも第 m 近接分子の分布を反映しません。 このことは特に密度を下げると顕著になります。 ρa = 0.4 の時、動径分布関数の第2ピークは x = 2.7 a にありますが、第2近接分子の分布のピークは x = 3.5 a、平均距離は 5.0 a と、大きく異なります。
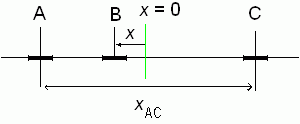
もう一つ興味深い問題として、3体の分布の問題を取り上げましょう。 3体分布というのは、3個の分子の間の相関を取り扱うもので、3個の分子に A、B、C と名前を付けたとすると、それぞれの分子間の距離 xAB、 xBC、xCA の関数として記述できます。 剛体棒流体においては3体の分布関数は2体の分布関数で表現でき、 3個の分子の配列の順序が決定的に重要になります。
xAB + xBC = xCA (5.1)
つまり B の分子が A と C の分子の間にある場合には、 3体の分布関数は次式のように表されます。
gABC(xAB, xBC, xAC) = g(xAB) g(xBC) (5.2)
2個の分子の配置を固定したときの、第3の分子の分布は次の条件付確率分布で与えられます:
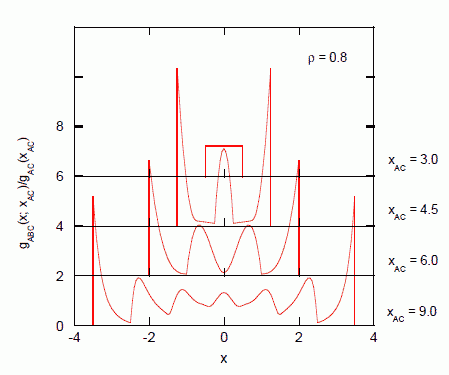
gABC(xAB, xBC, xAC)/g(xAC) = g(xAB) g(xBC)/g(xAC) (5.3)
この式から計算された、2個の分子 A、C の間に挟まれた領域における分子 B の分布を図に示します。 2個の分子間の距離とともに分子分布が劇的に変化することが見て取れます。 この2個の分子の間に挟まれた領域での分子分布の変化が、 2個の分子の間の動径分布関数の振動挙動と照応します。
なお3体の分布について Kirkwood の重ね合せ近似が用いられことがあります。 しかし Kirkwood の重ね合せ近似では、3体分布がすべての対についての2体分布関数の積 g(xAB) g(xBC) g(xAC) で表され、 剛体棒流体の3体の分布を正しく評価できません。 このことは熱力学量の加成則との関わりで重要な問題を提示するのですが、 ここではこの程度にしておきます。