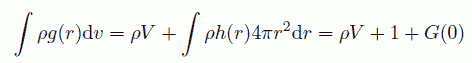付録：３次元の液体によるＸ線回折

Zernike-Prins の論文で、若干表記法が違うものの、すでに今日見るような形でのＸ線（あるいは中性子線）構造解析 の基本が議論されています。 Zernike-Prins の論文の最もよく知られている部分であるとは思いますが、 ここで３次元でのＸ線回折についての議論を紹介しておきます。

Zernike-Prins は３次元への拡張に際して、今日風に言うと全相関関数 h(r) = g(r) - 1 を導入して粒子数の揺らぎを議論します （Zernike-Prins は、全相関関数に数密度をかけたものを g₀(r) と表記して用いていますが、 ここでは今日通用の形にしておきます。 なお Ornstein-Zernike の論文では、g₀(r) を単に g(r) と表記していました）。 ２分子間の動径分布関数を全系にわたって積分すると、次のような表式を得ます。

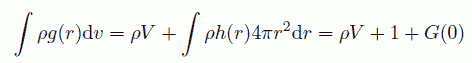　　(a.1)

ここで G(0) は粒子間の相関から来る寄与です。 これを明確にするために、 系をせいぜい１個しか分子の存在しない小さい領域に区切り、 粒子数の揺らぎを考えます。 m 番目の領域に存在する粒子数を γ_m とすると、 粒子数の２乗は次式で表されます （論文中では微小領域の体積と微小領域の密度の積を用いて表わしていますが、 ここでは簡単のため、微小領域の体積と微小領域の密度の積を単に γ_m で表記します）。

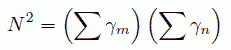　　(a.2)

この平均を計算する際、領域間の相関の項が現れてきます。 つまり γ_n = 1 の時、n と無関係に γ_m は決まらず、 その相関の寄与を表すのが先の G(0) であるという仕掛けです。

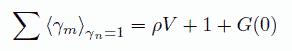　　(a.3)

ですから粒子数の分散を取ってみると、 分散は粒子数 N =ρV に 1 + G(0) (= S(0)) をかけたもので評価されます。

　　(a.4)

なお以上の粒子数揺らぎの話は蛇足とも思えるのですが、 Zernike は、光散乱と粒子数揺らぎを論じた Ornstein-Zernike の論文の内容をもう一度確認したかったようです。

図．　３次元での散乱では、入射線に対し φ/2 だけ傾いた面（図中青い線）を考えるのが便利。 ブラッグの反射条件が適用でき、面間の光路差は面間距離の関数 2x sin φ/2 で記述できる。

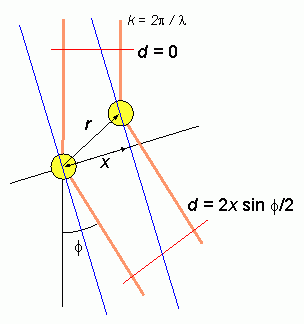
１次元の場合と３次元の場合で取扱いに注意しないといけないのは、 回折の際の条件の扱いです。 ３次元での光路差は、入射Ｘ線に対し回折角φの半分だけ傾いた面間の光路差を考えるのが便利です （つまりブラッグの反射条件）。 それぞれの面内の分子からの回折線は同じ光路差を持ち、 後で面に垂直な方向に積分を実行すればよいからです。 ですから次式で定義される量 s を用いて、式を展開していきます （今日、Ｘ線の分野では s ではなく k を、 中性子線の分野では Q を使用することになっています。 いつからそうなったんでしょう？）。

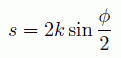　　(a.5)

まずそれぞれの面から回折されてくるＸ線の強度については、次の式を評価すればよく

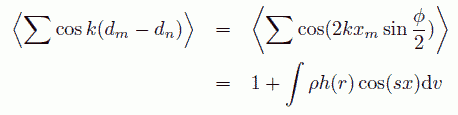　　(a.6)

これを全空間にわたって積分すれば、回折強度を導くことができます。 ここで積分をまず面に垂直な x 方向に対して半径 r の球面に沿って行っていることに注意します （dv = 2π r² sin θ dr dθ = 2π r dr dx。 今では見かけませんが、球対称な場合の３次元のフーリエ変換の表式の巧妙な導出法です。 昔はこうやって導出していたんでしょうか？）。

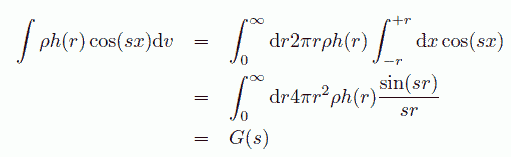　　(a.7)

最終的に回折強度は次式で表されます （構造因子 S(s) は 1 + G(s) に相当）。

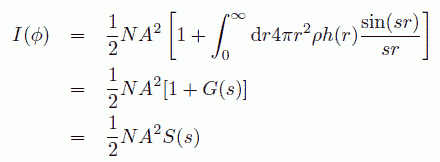　　(a.8)

Zernike-Prins は、実験的に得られる量として i(ｓ) を次式で導入しました（i(s) = G(s)） （この表記法を踏襲して、古い液体論の教科書には 構造因子 S(s) を使わずに i(s) で表記してあるものがあります。 他の記号と紛らわしいせいか今では見かけません）。

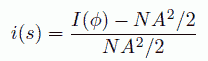　　(a.9)

そして全相関関数のフーリエ変換が、回折強度の角度（波長）依存性を与え、 回折強度の逆フーリエ変換が、全相関関数を与えるという関係式を導いて論文を閉じています。

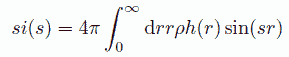　　(a.10)

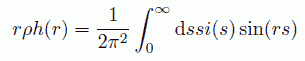　　(a.11)