2020.3
吉村洋介
積分幾何学のはなし

ビュフォンの針　幾何的な確率のこと

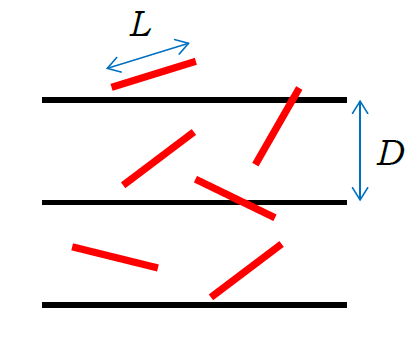
ビュフォンの針

幾何的な確率について、まず比較的有名な問題として、 ビュフォン Buffon の針の問題を取り上げましょう（18世紀から伝わる問題）。 ビュフォンの針の問題は、次のようなものです：

ビュフォンの針
間隔 \(D\) で引かれた平行線の上に、長さ \(L\) （\(L \lt D\)）の針を落とした時、 針が平行線と交わる確率はいくらか？ 		buffon
図0-1. ビュフォンの針

この問題をどう考えるかですが、針の中心の平行線からの距離と針の向き、 それぞれ無関係に、でたらめにふるまうと考えるのがよいでしょう。

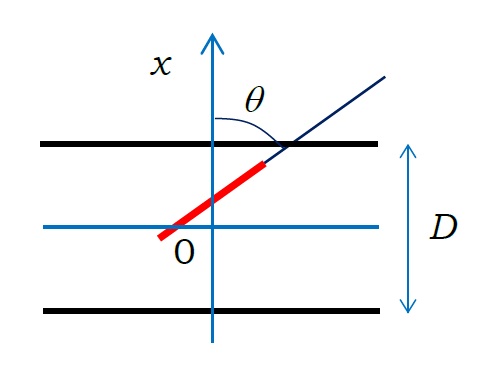
図0-2a のように２本の平行線の中線とそれに垂直に \(x\) 軸をとり、 針の中心は \(x\)軸上にあるものとします。 針の向きは針と \(x\) 軸のなす角度 \(\theta\) で示すことにします。 針の中心の位置 \(x\) と針の向き \(\theta\) が、 それぞれ独立にでたらめにふるまうというのは、 図0-2b の \((\theta,~ x)\) 座標上の \(0 \le x \lt D/2, ~~ 0 \le \theta \lt \pi/2\) の領域の中に、均一にばらまかれることだといってよいでしょう。 そしてその中で針が平行線と交わるのは、 \(x \ge (D - L \cos \theta)/2\) となる領域、 図0-2b の \((\theta,~ x)\) 座標上で黄緑に塗りつぶした領域です。

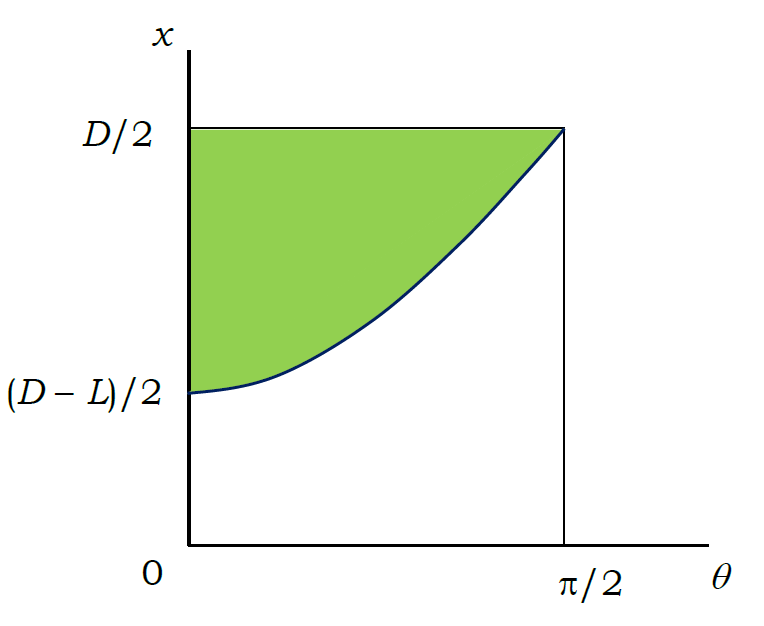
buffon coordinate buffon coordinate
図0-2a. 針の座標の設定。 \(0 \le x \lt D/2\)、\(0 \le \theta \lt \pi/2\) とする。 針の中心の位置 \(x\) が\((D - L)/2\) より大きくなると、 直線と交わるようになる。 図0-2b. 針が平行線と交わる\((\theta, x)\) 座標上の領域。 図の \(x \ge (D - L \cos \theta)/2\) となる 黄緑で塗りつぶした領域で針は平行線と交わる。

ですから針が交わる確率 \(P\) は、全領域に占める黄緑に塗りつぶした領域の割合を求めればよく、 \(\int_0^{\pi/2} \cos \theta ~\rmd \theta = 1\) に注意すると塗りつぶした領域の面積は\(L/2\) ですから、 次式で与えられます。

\begin{equation} P = \frac{L/2}{(D/2)(\pi/2)} = \frac{2L}{\pi D} \label{eq:buffonP} \end{equation}

ビュフォンの針とモンテカルロ計算

この問題は“実験的”に円周率を求める手法としても興味を持たれ、 実際に針を用いて数千回の実験を行って円周率を求めたという人もいるようです。 今日的には、計算機で乱数を発生させて、モンテカルロ法を適用するのがお手軽です。 後でも“実験”に触れるので、少し手法を詳しく紹介しましょう

ちょっと実際に計算の雰囲気を感じ取ってもらえるように、Javascript で計算するプログラムを作ってみました。 下記の試行回数に100000ぐらいの適当な数字を入れて、ボタンを押してみてください。

試行回数

重なり回数

図形の重み・測度をどう考えるか？

ビュフォンの針の問題は、針の位置と向きが\((\theta,~ x)\) 座標上に均一に分布すると考えて、 答えを導くことができました。 けれどもこれほど簡単な問題ばかりではありません。 後でも考えますが、たとえば平面上に２本の直線をでたらめに配置したとき、90°で交わる確率と、45°で交わる確率は同じでしょうか？ それともちがうでしょうか（図0-3）？ ２直線が平行なら交わらないわけですから、低角で交わる確率は小さいはずだという気がします。 でも「でたらめ」なのですから、どの角度も同等でないといけないはずです。 皆さんはどう考えますか？

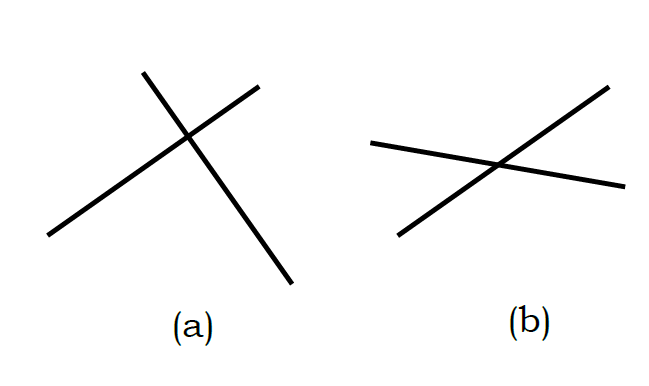
crossed lines 図0-3. ２本の直線をでたらめに配置した時、(a) 90°で交わる確率と、(b) 45°で交わる確率は同じでしょうか？ ２直線が平行（この確率は0とみなしていいでしょう）でなければ必ず交わります。 その交点に注目すると、直線はでたらめに配置しているわけですから、どの方位も等価です。 つまり (a) も (b) も同じ確率で出現するはずです！！？？
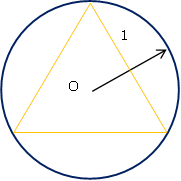
crossed lines 図0-4. Bertrand の弦： 半径 1 の円にでたらめに弦を引いた時、\(\sqrt{3}\) （図中の内接正三角形の一片の長さ）より大きくなる確率は？

あるいは図0-4の問題はベルトラン（J. Bertrand）の弦の問題として有名なものです（1907年刊行の Calcul des Probabilités という本にあるそうです）。 半径1の円にでたらめに弦を引いたとき、\(\sqrt{3}\) より大きくなる確率を求めようというのですが、 考え方によって1/3、1/2、1/4 とより取り見取りになるのが印象的です。


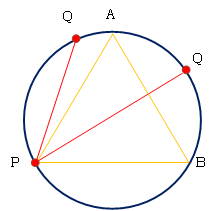
    bertrand a 図0-5a. 円周上に2点をでたらめに配置する。
  1. 【円周上の２点】
    円周上に２点 P と Q をでたらめに取ります。かりに P が図の位置にあるとすると、弦PQが\(\sqrt{3}\) より大きくなるのは、 P を頂点とする内接正三角形の弓型の円弧上に Q がある時。 つまり確率は 1/3 になります。
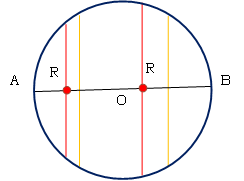
    bertrand a 図0-5b. 円を「千切り」にする。
  2. 【円を千切り】
    ある円の直径 AB をとります。AB 上の点 R に垂直な弦を取り、その長さが\(\sqrt{3}\) より大きくなるのは、R が円の中心から±1/2 の位置にある時。 つまり確率は 1/2 になります。
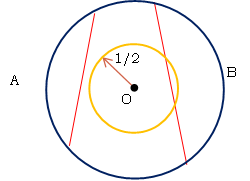
    bertrand a 図0-5c. 弦の中心の占める領域に注目する。
  3. 【弦の中心の存在領域】
    弧に円の中心から下ろした垂線の足 H に注目します。 垂線の足の位置が決まれば弧は決まります。 弧の長さが\(\sqrt{3}\) より大きくなるのは、H が円の中心から1/2 以内にある時。 つまり確率は H の存在する領域の比率、1/4 になります。

こうした問題を考えるポイントは、「でたらめ」がどうでたらめなのか、ということにあるといっていいでしょう。 たとえば２本の線分の交わる角度の出現確率やベルトランの弦の問題を学生さんに聞いてみると、 「コンピューターにでたらめに直線を発生させて計算させればよい」といった答えが出てきたりします。 モンテカルロ法などをかじったことがあれば、当然出てくる答えではあるのですが、 ではどうやって「でたらめに直線を発生」させるのか？

たとえば平面上の直線の方程式を \(ax + by + c = 0\) として、\(a\), \(b\), \(c\) に [-0.5, 0.5) の一様乱数を割り当てればよいのでしょうか？ このようにすれば、平面上のすべての直線が「でたらめ」に出現するわけですからよさそうにも見えます（切片も勾配も \(\pm \infty\)の範囲を取ります）。 図にはこの考えに従って発生させた直線を描いてみました。 一見「でたらめ」のように見えるかもしれません。 でも原点付近に線が密集しているのはどうでしょう。 本当に「でたらめ」なら、直線と原点の距離に何の制限もないわけですから、 図に示す原点付近の±3 ぐらいの領域に直線を見出す確率はゼロのはずですよね？ （さらに詳細にみると45°方向に少し分布が偏っています。）

random lines 図0-6. 直線の方程式 \(ax + by + c = 0\) のパラメーター \((a, b, c)\) に [-0.5, 0.5) の一様乱数を割り当てて生成した1000本の直線を、 原点を中心とする一辺の長さ6の正方形の領域（\((-3, -3) - (3,3)\)）について描いたもの。 原点付近に直線の出現頻度が偏っている。
表紙のページへ　　　　次のページへ