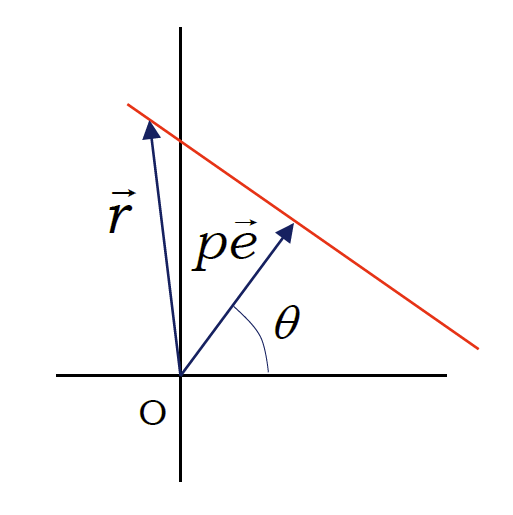
図1-1. ヘッセの標準形。 \(\vec{r} = (x, y)\)、\(\vec{e} = (\cos \theta, \sin \theta)\)
平面上の直線の重み、測度というのを考えるとき、 直線を平行移動しても、回転させても、その重みが変わらないことが期待されます (幾何で三角形の合同を示すのに、平行移動と回転を行って重ね合わせることに相当するといってよいでしょう)。 先ほどの「でたらめな」直線の発生法で考えた、パラメーター\(a, b, c\) に [-0.5, 0.5) の一様乱数を割り当てた直線の方程式 \(ax + by + c = 0\) に即して考えてみると、 これを\(x\) 方向に \(x_0\) だけ平行移動して得られる直線の方程式は次のように書けます。
\begin{equation} a x + b y + (- a x_0 + c) = 0 \end{equation}
この式で \(|-a x_0 + c| \gt 0.5\) であると、元の式のパラメータの値域を越えてしまいますから、 元の式に焼き直すには、パラメータ \(a, b, -a x_0 + c\) 全体をスケールして縮小しないといけません。 つまり元の式で\(\rmd a~ \rmd b ~\rmd c\) という重みがあったのを、小さくしないといけない。 あるいは元の \(| c| \le 0.5\) であった領域の重みを増やさないといけない。 これは先の図で、中心付近が濃くなっていた(中心の方が重みが大きい)ことに対応します。
図1-1. ヘッセの標準形。 \(\vec{r} = (x, y)\)、\(\vec{e} = (\cos \theta, \sin \theta)\)
それでは、直線を均一に配置するにはどのように考えればよいでしょう。 ここで登場するのが、直線の方程式のヘッセの標準形(Hesse normal form)と言われるものです:
\begin{equation} x \cos \theta + y \sin \theta = p \label{eq:hesse} \end{equation}
ここで \(p\) は原点から直線に下した垂線の長さ(直線との距離)で、\(\theta\) は垂線と \(x\) 軸の角度に相当します。 ここで用いられているパラメータ \(p, \theta\) について重み、測度 \(\rmd p ~\rmd \theta\) を考えると、 これは平行移動しても回転しても変わらないのです。 これを確認するには、式\eqref{eq:hesse} のヘッセの標準形で表された直線上の点に回転と平行移動をかけて、 \((X, Y)\) という位置に移動させ、その結果次の直線になった状況を考えてみればよいでしょう。
\begin{equation} X \cos \theta' + Y \sin \theta' = p' \label{eq:hesse2} \end{equation}
ここで\((X, Y)\) は、\((x, y)\) を \(\alpha\) 回転させて \((u, v)\) だけ平行移動させたもの、 とすると次のように表されます:
\begin{equation} \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) + \left( \begin{array}{c} u \\ v \end{array} \right) \label{eq:rottrans} \end{equation}
式 \eqref{eq:hesse2} が行列を使うと次のように書けることに注意すると
\begin{equation} \left( \begin{array}{cc} \cos \theta' & \sin \theta' \end{array} \right) \left( \begin{array}{c} X \\ Y \end{array} \right) = p' \end{equation}
式 \eqref{eq:rottrans} を代入して容易に次の関係が得られます:
\begin{equation} x \cos (\theta' - \alpha) + y \sin (\theta' -\alpha) = p' - (u \cos \theta' + v \sin \theta') \end{equation}
式\eqref{eq:hesse} がこれと一致しているわけですから、 測度 \(\rmd p \rmd \theta\) と\(\rmd p' \rmd \theta'\) の関係を見るには、微分形式を使って書くと (ヤコビアンを使っても同じことですが面倒なので)
\begin{eqnarray} \rmd p \wedge \rmd \theta &=& \rmd [p' - (u \cos \theta' + v \sin \theta')] \wedge \rmd (\theta' - \alpha) \\ &=& [\rmd p' - (-u \sin \theta' + v \cos \theta') \rmd \theta'] \wedge \rmd \theta' \\ &=& \rmd p' \wedge \rmd \theta' \end{eqnarray}
より、重み \(\rmd p \rmd \theta\) が回転・平行移動で変化しないことが分かります。 2次元の場合には、回転・平行移動で不変な直線の測度として、この形のものしかないことが知られています。
ヘッセの標準形の形で表した直線について、その測度として\(\rmd p \rmd \theta\) をとることで、 回転・平行移動で不変な直線の測度が得られることを見たのですが、 その具体的な例として先に挙げたベルトランの弦の問題を取り上げてみましょう。
もうお分かりでしょうが2番目のアプローチ、ある直径に垂直な弦を考え、中心からの距離の関数と考えるというのが、 ヘッセの標準形から導かれる測度 \(\rmd p ~\rmd \theta\) に対応していて、 「でたらめに」弦を引くという趣旨にかなっていると言えるでしょう。 弦の出現確率分布を考えると、分布関数(確率密度)は \(0 \le p \le 1\), \(0 \le \theta \lt 2\pi\) として
\begin{equation} f(p, \theta) = \frac{1}{2\pi} \end{equation}
で一定というわけです。 では他のアプローチはどうか、少しかみ砕いて見てみましょう。
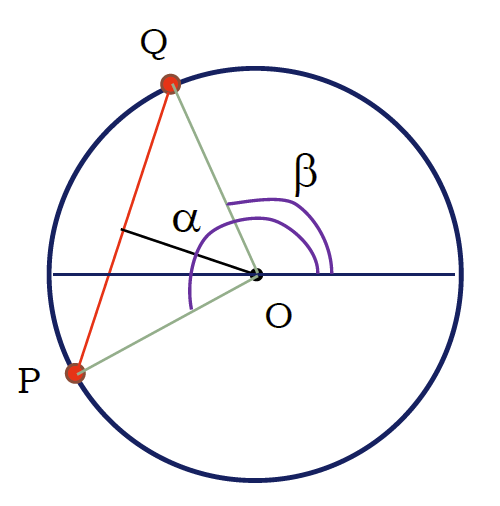
図1-2. ベルトランの弦の問題で円周上のでたらめな2点をとった場合の測度は \(\rmd \alpha ~\rmd \beta\) 。
円周上にでたらめに2点を取って弦を引くというのは、 原点の周りの2点の角度を\(\alpha\)、\(\beta\) とすると(\(\alpha \gt \beta\))、 弦の測度を\(\rmd \alpha ~\rmd \beta\) で与えていることになっています。 これを\(p, \theta\) で表してみると次のようになります:
\begin{eqnarray} \alpha = \theta + \cos^{-1} p \\ \beta = \theta - \cos^{-1} p \label{eq:dJdt} \end{eqnarray}
ですから、この測度を\(\rmd p ~\rmd \theta\) で表すと
\begin{eqnarray} \rmd \alpha \wedge \rmd \beta &=& \left( \rmd \theta + \frac{\rmd p}{\sqrt{1 - p^2}} \right) \wedge \left( \rmd \theta - \frac{\rmd p}{\sqrt{1 - p^2}} \right) \\ &=& \frac{2}{\sqrt{1 - p^2}} \rmd p \wedge \rmd \theta \end{eqnarray}
つまり円弧上の2点に弦を対応付けるアプローチでは、 分布関数は次のようになります
\begin{equation} f(p, \theta) = \frac{1}{\pi^2 \sqrt{1 - p^2}} \end{equation}
\(p\) の大きいところ、円の中心から離れたところの重みが過大に評価されます。 したがって円の中心から離れた短い弦の重みが大きくなり、\(\sqrt{3}\) より長い弦を見出す確率(\(p \le 0.5\) となる確率)が低く算定されたというわけです。
垂線の足までの距離が1/2以内の領域に注目するというのは、 目の付け所としては面白いのですが、 垂線の足、点の存在する領域に注目した結果、 測度が\(\rmd (p^2 /2) ~\rmd \theta\) となり、 分布関数は次のようになります
\begin{equation} f(p, \theta) = \frac{p}{\pi} \end{equation}
同様に \(p\) の大きいところ、円の中心から離れたところの重みが過大に評価され、 \(\sqrt{3}\) より長い弦を見出す確率が最も低く算定されたわけです。
最後に以上の結果を図にまとめておきましょう。 図形の重みをどのように評価するかが、 いかに重要かを感じ取っていただければ幸いです。
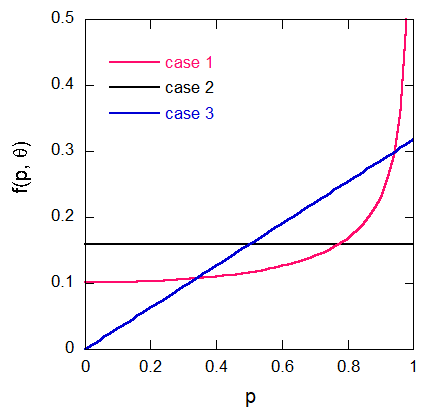
図1-2. ベルトランの弦の問題の種々の解の \((p, \theta)\) での分布関数。
case 1(赤): 円周上にでたらめに2点を取った場合、
case 2(黒): 円を千切りにした場合、
case 3(青): 弦の中心の存在範囲を取った場合