図 1. 物質の三態とその分子配列 |
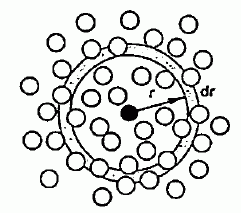
図 2. ある分子周りの分子の分布 |
私は中性子回折でいろんなものの構造や物性を調べてきました。 実は昨年、高エネルギー研究所から、新潟大学に移ったばかりで、あまり新しいお話はできないのですが、 きょうは、回折実験による液体構造研究の基礎的なところから始めて、四塩化炭素の液体構造を中心にお話ししたいと思います。
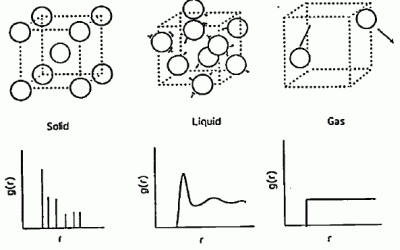
まず、釈迦に説法というたぐいの話になるかもしれませんが、 結晶・液体・気体の分子の配列の概念図のようなものを図 1 に示します。 結晶の場合には、分子はある決まったところにいますし、 気体の場合には互いにバラバラの配置をとり、液体の場合には、 何かある構造を持っているようでいてそうでもない、というわけです。 こうしたそれぞれの状態を記述するものとして、動径分布関数があります。

図 1. 物質の三態とその分子配列 |

図 2. ある分子周りの分子の分布 |
ある分子から距離 r 離れたところで、 微小な距離 dr の間に見いだす分子数 n(r) dr を考えます。 かりにそこでの単位体積あたりの分子数(数密度)が、 体系全体についてならした値 ρ と等しければ、 見いだす粒子数は、考える領域の体積 4πr2 dr に ρ をかけたものになります。 けれども、構造があればそれは平均値からはずれ
![]() (1)
(1)
といった形で表現されることになります。 この平均値と実際に見いだす粒子数の比を表わす関数 g(r) を、動径分布関数と呼びます。 この動径分布関数を使えば、さきの結晶・液体・気体というのは、図 1 の下段のように特徴付けられることになります。 気体の場合には、構造がないので分子コアの外は平均密度と同じ、 つまり g(r) = 1 です(簡単のため剛体球分子を考えます)。 結晶の場合は分子はある決まった位置に分布しますから、動径分布関数は、とびとびの値を取ります。 そして液体の場合は、連続的でありながら何かしら構造を含むということになるわけです。
ではこの液体構造を、いかに観測するかですが、 これには中性子線、X線の回折現象が利用できます。 以下では、中性子の場合についてお話しします。
皆さんは、結晶の構造解析で、ブラッグの反射条件というのをご存知のことと思います。 距離 d の間隔で並んでいる原子面に、その面に対し角θで入射する、波長λの中性子線を考えると、
![]() (2)
(2)
を満たす条件で、強い回折波が観測されます。 液体の場合にも、基本的には同じ考えを適用できます。
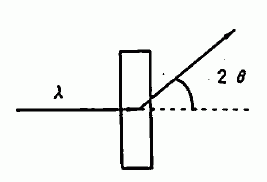
液体に対する中性子線の回折実験は、簡単に言うと図3のようなものです。 左の方から中性子線を当てて、角度 2θ(入射角と反射角の和に相当)の方向に回折されてくる中性子の強度を観測しています。 ここで、中性子の波長と、回折角という2つの変数があるわけですが、(2)式からもわかりますように、構造を議論する上では
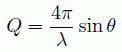 (3)
(3)
で定義される、波数 Q (= 2π/d)の形で議論すれば十分です。 実験ではこの Q を、角度を変えるか、中性子の波長(中性子のエネルギー)を変えるかして変化させ、 その時の1個の中性子あたりの回折強度 I(Q) をいろんな Q について調べます。 この I(Q) が、その液体の成り立ちを反映するところから、いろんな化学や物理が始まることになります。