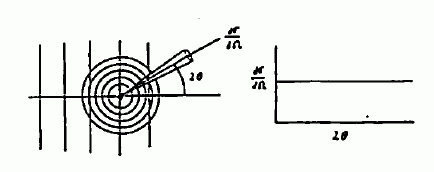
図 4. 1個の原子核による中性子の散乱
まず1個の原子核への、中性子の衝突を考えましょう。

中性子が原子核に衝突する時、原子核と中性子とで核反応が起きることもありますが、 たいていは反応など起こさず散乱されて出てきます。 この中性子を散乱する能力(散乱長)は、原子核の種類によってさまざまです。 けれども注意していただきたいのは、散乱された中性子がどの方向に出てくるかは、 角度によらず一定だということです(図 4)。 ですから、1個の原子核による中性子の回折実験をして I(Q) を測っても、それは Q によらず、一定値をとります。 しかし近くに他の原子核がありますと、後で示す図 5 のように散乱された中性子の間で干渉が起きることになり、 事態は単純でなくなります。 光の回折現象でいう、ホイヘンスの原理を思い起していただけるとよいでしょう。
この干渉の効果を定量的に取り扱ってみると、次のようになります。
ある波数 Q で回折されてくる中性子の割合は、各原子核で散乱されて出てくる波を重ね合せたもの F(Q)
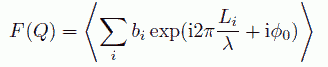 (4)
(4)
に比例します。 ここで、bi は i 番目の原子核の散乱長、Li はその原子核で散乱された中性子が、検出器に到達するまでの距離、 中性子の初期位相は揃っているとし、それを φ0 とおいてあります。 また液体中で原子はあちらこちらに動き回っているわけですから、 その統計平均をとる必要があり、< > は統計平均を示しています。
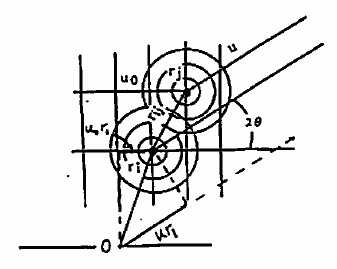
この多数の波の重なりを見るわけですが、光の干渉を考えるのと同様、 問題はそれぞれの波の間の位相 2πLi/λ のちがいです。 図 5 のように、u0 の方向からきた中性子が、u の方向に回折される場合を考えます (u0、u は単位ベクトル)。 この時原点で回折される中性子の行程と、ri で回折される中性子の行程の差は
![]() (5)
(5)
になります。 これは位相の違いでいうと次のように書けます。
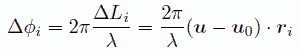 (6)
(6)
u - u0 の大きさは、2 sin θ ですから、(3)式で考えた Q をベクトル化して
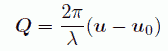 (7)
(7)
で定義すると、原点で回折される中性子を基準にとった位相の違いは
![]() (8)
(8)
と簡単に書けることがわかります。ここで、原点での位相が 0 になるとして、(4)式を書き直し次式をえます。
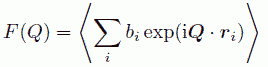 (9)
(9)
観測されるのは回折波の強度 I(Q) ですから、F(Q) の絶対値をとる必要があります。
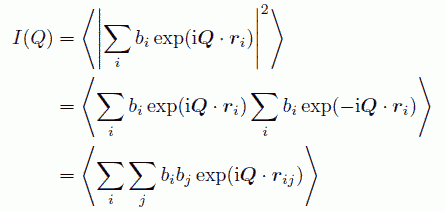 (10-12)
(10-12)
ここで、原子核 i と j の相対位置を示すベクトル rj - ri を rij としました。 ところで、分子がばらばらに存在しているとした時の回折強度は、 含まれている各原子核の散乱長の平均値 < b > (= Σbi/N) の2乗 < b >2 の N 倍で評価できます。 これを使って I(Q) を規格化したものを構造因子 S(Q) と呼び、これが液体構造を議論する出発点になるわけです。
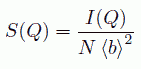 (13)
(13)
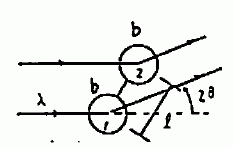
実際の系の構造因子を考えるには、(12)式中の平均化操作の中味にさらに踏込んで議論しないといけません。 式のままでは抽象的ですから、具体的に右図のように、 結合距離 l の等核2原子分子が1個存在する場合について考えてみます。 (12)式で総和を取る部分はそれぞれの原子核ですから、全部で 2×2 = 4 項出てきて、整理すると、
![]() (14)
(14)
ここで角度φは、Q ベクトルと2原子分子の軸とのなす角で、 指数の中に入っている Ql cos φ は、ベクトル Q と 2原子分子の軸方向のベクトルの内積です (散乱角 2θ とφは別物であることに注意してください)。 ここで、核の配置について平均をとる、つまり分子の向きについての平均をとります。 分子はすべての向きを同じ重みでとりますから、極座標系を用いて、
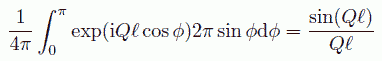 (15)
(15)
であることから、最終的に構造因子の形で書くと、
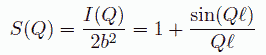 (16)
(16)
となります。 これを図 7 に示します。 この図の山の間の間隔が、2πを結合距離で割ったものに等しくなります。 透過力が弱いので、液体の構造の研究には用いられていませんが、電子線回折による分子構造の研究では、 ちょうど図 7 のようなものを見ていることになっています。
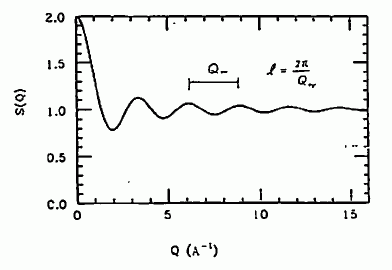 図 7. 2原子分子の構造因子 (l = 2.7 Å)
図 7. 2原子分子の構造因子 (l = 2.7 Å)
上で考えたのは、ある原子から見て、1個の原子が距離 R 離れたところにある、 つまり原子の分布という観点からいうと、距離 R のところに大きな密度で原子が存在し、 それ以外では密度 0 という状況についての話でした。 しかし液体では、近傍だけでなく、その外側にも多数の原子がひしめき合っています。 こうした場合について、今度は単原子分子からなる純液体(希ガスなど)の場合について考えてみます。
一成分で考えていますから、構造因子は散乱長の影響をうけず、次式で表現できます。
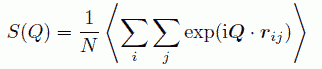 (17)
(17)
ここで、(15)式で考えたように、方向についての平均化を行い、i = j(つまり rij = 0)の因子を分けて
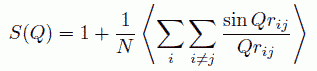 (18)
(18)
第2項について、それぞれの核は等価ですから、i = 1 の場合について j = 2 から N までの和をとったものは、 i = k について j = 1 から N まで、j = k のものを除いて和をとったものに等しいので、 rj = r1j とおき、
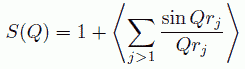 (19)
(19)
ここの平均化の操作を考えてみると、それはある原子から見て距離 r のところに粒子を何個見いだすかを考え、 それに sin(Qr)/Qr という因子をかけて足しあわせたものです。 ですから(1)式を用いて(19)式は次のように書き表せます。
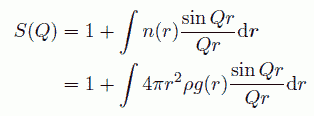 (20)-(21)
(20)-(21)
このように回折実験から求まる構造因子と、動径分布関数とが密接に関係していることがわかります。 ところで(21)式では、Q = 0、つまり回折されるものの、そのまま真っ直ぐ出てくる場合に、 構造因子が粒子数 N に比例する、大きな値をとることになります。 これは、Q = 0 では散乱中性子間の位相のずれがまったく起きないためで、 分子の分布に相関のない場合の散乱、つまり g(r) = 1 とした場合には、この Q = 0 の回折しか現れません。 また実際に観測する分には、Q = 0 の回折というのは、回折されないで透過してくる中性子と区別できません。 したがって、通常、 g(r) = 1 とした回折の効果を(21)式から差し引いて
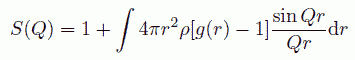 (22)
(22)
で構造因子を記述します。 なお、S(0) として取り扱われる量は、(22)式(あるいは(21)式)で Q を 0 に近づけていった極限値に相当します。
さて(22)式は、フーリエ変換の形になっています。 ですからこれを逆変換すれば、動径分布関数が得られることになります。つまり
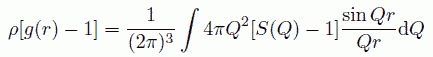 (23)
(23)
で、動径分布関数がえられるわけです。
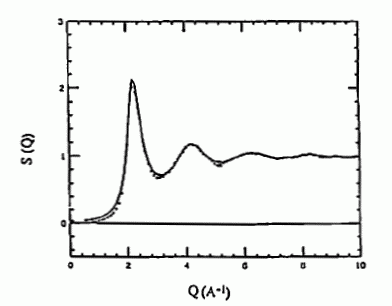
このような単純液体については、すでに多くの研究がなされています。 図 8 に単純液体の典型として、液体タリウムの構造因子を示しました。 このような単純液体の研究で明らかになったことで、 特に重要なのは、剛体球(パチンコ玉)からなる流体が、現実の液体のよいモデルとなることです。 そして剛体球流体の構造因子 Shs(Q) に少し手を加えた、次のような関数で、 現実系の構造因子が、きわめてよく再現されることが知られています。
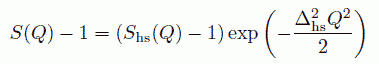 (24)
(24)
ここで右辺の Δhs は、分子の柔らかさを示すパラメーターです。
剛体球流体の構造因子をどう評価するかが問題ですが、
これについては理論的に詳細な検討がなされています。
そうした中で、パーカス-イェビック(PY)近似は解析的な形で S(Q) が表現でき、
かつ計算機実験で得られる剛体球流体の S(Q) との一致もよいので、
よく用いられています。