|
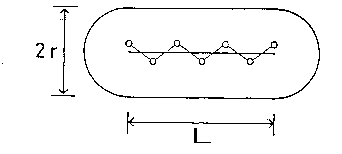
| 図5.8 n-アルカン分子のコアのモデル。 シリンダー部分の長さ \(L\) は \((n-1)d\) に等しくとる。 ここで \(d\) はメチレン鎖の繰り返し単位の長さの半分で 127 pm である。 分子の”厚み” \(r\) には、結晶のパッキングから 229 pm を用いる。 |

|
| 図5.8 n-アルカン分子のコアのモデル。 シリンダー部分の長さ \(L\) は \((n-1)d\) に等しくとる。 ここで \(d\) はメチレン鎖の繰り返し単位の長さの半分で 127 pm である。 分子の”厚み” \(r\) には、結晶のパッキングから 229 pm を用いる。 |
アルカン分子と他の分子との相互作用を考える上で、アルカン分子のコアを何らかの形で設定することができれば便利である。 もっとも単純なコアとして図 5.8 のように、半径 \(r\)、長さ \(L\) の円柱の両端にやはり半径 \(r\) の半球を取り付けたものを考える。 このコアのモデルではメチレン基はシリンダ-部分に、メチル基は端の半球とシリンダ-の一部とを割り当てられている。 実際のアルカン分子の分子軸に垂直な断面は円ではなく楕円に近く、末端部のメチル基を半球とみなすにしてもその中心は分子軸上からはずれたところにあると考えるべきである。 ここで用いるモデルはこのために実際のアルカン結晶で観察されている炭素数の偶奇による結晶型の変化などは説明できない。 しかし、後でも触れるように部分分子容の加成則を議論する分にはこれで今のところは十分である。
今回のモデルの具体的なサイズは次のようにして決めた。 シリンダ-部の長さはアルカンのジグザグ鎖の繰り返し単位を \(2d\)、炭素数を \(n\) として\(L = (n - 1)d\) であると考えることができる。 この繰り返し単位の長さはアルカン結晶の分子軸方向の長さのデ-タから 254 pm であり \(d = 127 ~\mrm{pm}\) と定まる。 問題は、シリンダ-・半球の部分の半径 \(r\) である。 この値はシリンダ-部分を最も密に詰めたときそのパッキング率、つまり分子コアの体積 \(V_\mrm{C}\) とそれが示す結晶の体積 \(V\) の比が
\begin{equation} \frac{V_\mrm{C}}{V} = \frac{2 \sqrt{3}}{\pi} \label{eq:5.4.1} \end{equation}
となることと、アルカン結晶について室温付近での結晶の分子容の加成則からメチレン基あたり 13.9 cm3 mol-1 (三斜晶系結晶についての値 13.8 cm3 mol-1 と斜方晶系結晶についての値 14.0 cm3 mol-1 との平均値) という値がえられることから 229 pm と定めた。
このようなアルカン分子のコアのモデルを用いて、3、4章で考えたような剛体分子からなる溶媒中でのアルカン分子の挙動を考えていくことにする。
部分分子容の加成則は分子各部がそれぞれ独立に部分分子容に寄与することを意味している。 そしてこのことは、5.2節でみたように無限希釈状態でアルカンの部分分子容に対する加成則がきわめてよく成立するという実験的な裏付けをもっている。 したがって、アルカン分子末端の半球部分そしてシリンダ-部分がそのコアの体積をどの程度、部分分子容に反映するものかを見積ることができる。
アルカンの今回のモデルに基づいて分子各部の部分分子容への寄与の度合をみつもることを考えよう。 このような観点からは部分分子容は次のように表現される。
\begin{equation} \bar{V} = \kappa_T k_\mrm{B} T + a_1 \pi r^2 d (n-1) + a_2 \frac{4 \pi}{3} r^3 \label{eq:5.5.1} \end{equation}
先の \(\alpha\)、\(\beta\) は、この式から
\begin{equation} \alpha = a_1 \pi r^2 d \label{eq:5.5.2} \end{equation} \begin{equation} \beta = \kappa_T k_\mrm{B} T + a_2 \frac{4 \pi}{3} r^3 - a_1 \pi r^2 d \label{eq:5.5.3} \end{equation}
で表現されることになる。 つまり \(\beta\) には \(\alpha\) と異なり半球部分の寄与が含まれている。 \eqref{eq:5.5.1} 式と5.2 節で決めた 25 °C 、1 atm シクロヘキサン中のアルカンの部分分子容の加成則からこの \(a_1\)、\(a_2\) を求めると
\begin{equation} a_1 = 1.32 \label{eq:5.5.4} \end{equation} \begin{equation} a_2 = 1.54 \label{eq:5.5.5} \end{equation}
ということになる。 これからシリンダ-部分の方が末端の半球部分に比べて部分分子容への寄与が小さい、つまりよりよくパッキングされていることがわかる。 5.3 節で \(\beta\) の温度・圧力依存性がより大きいことをみた。 それはこの \(a_1\)、\(a_2\) という視点からみれば \eqref{eq:5.5.2}、\eqref{eq:5.5.3} 式から末端の半球部のパッキング率の温度・圧力依存性がより大きいことに相当するわけである。
こうしてみると、従来、共通体積と呼ばれてきたものの起源もおのずと明らかである。 Traube の考えによれば分子を構成する各原子(アルカンについては炭素原子と水素原子)は分子のどの位置にあろうと、部分分子容に対して同じだけの寄与をするのであった。 あるいは、今回のように分子のコアの体積を考える寺沢らの扱い[5.3]によれば、 ファンデルワ-ルス体積が部分分子容におよぼす寄与は分子の形によらず一定なのであった。
今回の結果は、分子各部に部分分子容に対する独立の寄与を割り当てることは妥当であるが、その寄与のしかたはその部分の"かたち"に依存することを示している。 従来の枠組で共通体積などという形で処理されてきたものは、部分分子容への並進の寄与に加えて分子各部のパッキングのされ方の相違を押し込めたものと考えることができる。 具体的にいうと今回のモデルからの式\eqref{eq:5.5.1} は、部分分子容への配置の寄与に注目すれば
\begin{equation} V(\mrm{conf}) = a_1 \left[ \pi r^2 d ( n-1) + \frac{4 \pi}{3} r^3 \right] + (a_2 - a_1) \frac{4 \pi}{3} r^3 \label{eq:5.5.6} \end{equation}
この式で \(a_1\) が 5.1 節で取り上げた寺沢らの扱い[5.3]では \(a\) に、 また第二項に並進の寄与を加えたものが \(b\) にそれぞれ対応することになる。 つまり、並進の寄与を無視すれば、アルカンについての共通体積なるものはアルカン分子のシリンダ-部分と半球部分の、 つまりメチレン基部分とメチル基部分のパッキングの相違から生まれてきた量なのである。
ある系の中に、溶媒分子 S とまったく相互作用しない溶質分子 X が存在するとき、この溶質分子の示す部分分子容の値は1章でのべたように \(\kappa_T k_\mrm{B} T\) に等しい。 今、この X 分子が溶媒と相互作用するようになったとしよう。 このとき全系のギブス自由エネルギ-の増分を \(W\) とすれば X の部分分子容は \(\partial W/\partial P\) だけ増加する。 つまり、X の部分分子容は次のように書ける。
\begin{equation} \bar{V} = \kappa_T k_\mrm{B} T + \pdif{W}{P} \label{eq:5.6.1} \end{equation}
この表式のすぐれた点はよく用いられるエネルギ-的な視点を部分分子容の解釈に持ち込めることにある。 溶質と溶媒との相互作用を付加するさいに、次の二段階で行なうものとしよう。
|
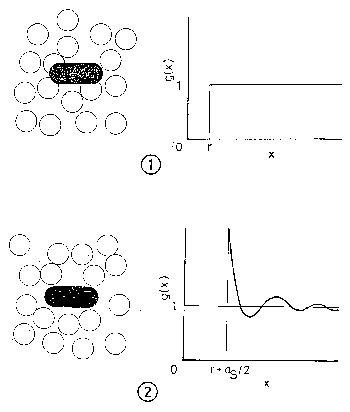
図 5.9. 溶媒中に分子コアを形成する2つのステップ。 (1) 溶媒の構造を変化させることなく分子コアを形成する。 (2) 分子コアの周りに溶媒分子による液体構造を形成する。 (1) では溶媒の分布は変化しないとしているので、分子コアの周りの溶媒分子の分布は溶媒の1体の分布関数の値 1 になる。 もし考えるコアが広い平らなきわめて薄い板であればこの (2) の過程は液体中に界面を作る過程にちょうど対応する。 |
それぞれの過程に相当する概念図を図 5.9 に示した。 ①の過程では分子コアの周りには溶媒分子の構造は存在しない。 そのため図にあるように、溶媒分子のコアと溶質分子のコアとの重なりも起きることになる。 ②の過程は①の状態から溶媒分子の再配列を行なう過程であり、この過程が結局パッキングを決める過程ということになる。 この①の過程にともなう可逆的仕事、ギブス自由エネルギ-変化は、\(PV_\mrm{C}\) に等しい。 ②の過程にともなう可逆的仕事が結局問題になるわけだが、ここでは巨視的物体とのアナロジ-で界面エネルギ- \(\gamma S_\mrm{C}\) を用いて見積ることにする[5.13]。 界面エネルギ-は、溶媒内にある界面を作りだすのに必要なエネルギ-であり、それはちょうどここで問題にしている構造を持たない溶液に構造を持たせるためのエネルギ-に相当している。 なお \(\gamma\) は剛体平面と溶媒との間の界面張力であることに注意されたい。
前節の分子コアについて \(W\) を計算すれば次のようになる。
\begin{eqnarray} W &=& P V_\mrm{C} + \gamma V_\mrm{C} \nonumber \\ &=& P \left[ \pi r^2 L + \frac{4 \pi}{3} r^3 \right] + \gamma \left[ 2 \pi r L + 4 \pi r^2 \right] \label{eq:5.6.2} \end{eqnarray}
したがって、部分分子容の表現としては配置の寄与に注目して
\begin{eqnarray} \bar{V}(\mrm{conf}) &=& V_\mrm{C} + \pdif{\gamma}{P} S_\mrm{C} \nonumber \\ &=& (1 + 2y) \pi r^2 L + (1 + 3y) \frac{4 \pi}{3} r^3 \label{eq:5.6.3} \end{eqnarray}
ここで\eqref{eq:5.6.3}式の中で
\begin{equation} y = \frac{1}{r} \pdif{\gamma}{P} \label{eq:5.6.4} \end{equation}
と略記した。 前節の表式と合せてみれば、分子の各部のパッキングのされ具合を示す \(a_1\)、\(a_2\) は
\begin{equation} a_1 = 1 + 2y \label{eq:5.6.5} \end{equation} \begin{equation} a_2 = 1 + 3y \label{eq:5.6.6} \end{equation}
となる。 つまり実際に観察される \(a_1 \lt a_2\) という傾向がこれで示されたことになる。 この手法で現われたアルカン分子の各部のパッキングの相違は、各部の表面積と体積との比に起因している。 すなわちここの扱いでは、表面積が体積に比べて大きければ大きいほどパッキングされにくいのである。
なおここで、\(\partial \gamma/\partial P\) という値を問題にしたわけだがこれをシリンダ-部分についての値 \(a_1\) を用いて見積ると 37 pm、 半球部分についての値 \(a_2\) を用いて見積ると 41 pm という結果を与え、両者の一致はよい。 さらに実験的に知られている界面張力の圧力依存性は、たとえばシクロヘキサン-水界面について \(\partial \gamma/\partial P\) は 25 °C、 1 atm で 30.4 pm であり[5.14]ここでの取扱いから得られた結果の妥当性を裏付けている。
ここで、分子間の引力的な相互作用については何ら考慮することなく分子各部のパッキングの相違が導き出されたことに注目したい。 一つの考えとしてアルカン分子と溶媒分子の間の相互作用ポテンシャルエネルギ-の谷がメチレン基の周りの方がメチル基の周りより深いことから、 メチレン基がよりよくパッキングされることを想定することが可能である。 しかし、このような効果は斥力的な効果に比べて極めて小さい。 実際、摂動論的な立場からこの効果を見積ってみるとたかだか数パ-セントの効果しかパッキングに及ぼさないことがわかる。 引力的相互作用の効果は、大きな静電的相互作用の期待できるような系でない限り分子各部のパッキングの相違を説明するものではない。 これは、ファンデルワ-ルスの描像からも首肯されるところである。