|
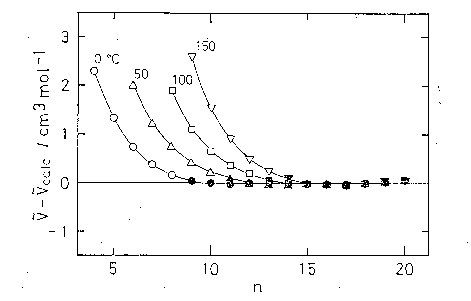
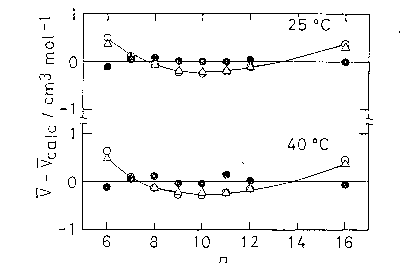
図 5.1. 純 n-アルカン液体の分子容の加成則からのはずれ。 加成則からの計算値を得るのに用いた加成則の係数は、その温度で液体であるアルカンの内、 沸点のより低い 5 個のアルカン(図中の白抜きの点)を除いたものについて1次関数に最小二乗法でのせることにより得た。 用いた分子容の値は [5.4]による。 |
古くから(部分)分子容をその分子の成り立ちから説明しようとする試みが行なわれてきたが、その根幹をなすのが部分分子容の加成則である。 部分分子容の加成則はある化合物の部分分子容が化合物を構成する原子・基からの寄与の和であるとする。
巨視的な物体の場合にはその体積は物体各部の体積の単純な和であり、体積は物体各部からの独立の寄与の総和であると考えることができる。 (部分)分子容の加成則の背景にはこうした巨視的物体との単純なアナロジ-がある。1章でも述べたようにこのような考えは原理的には誤っている。 しかし現実にはこの巨視的な物体とのアナロジ-がよく成立するように見受けられるし、この加成則に基づくさまざまな分子論的な議論が行なわれても来たのである。 この章ではこれまで数多くの実験デ-タが集積されているアルカンについて加成則はどの程度まで成立するのか、 またどのような条件下で成立するのかを等温・等圧の条件下で検討し、その分子の形との関わりを検討する。
(部分)分子容の加成則の研究は、分子容については 150 年、部分分子容についても 100 年近い研究の歴史を持っている。 特に19世紀はその最もはなやかな時代であった。 しかし、その後の化学の変貌はこのような研究を色あせたものにし、加成則に対する研究は多く忘れられていった。 今日の物理化学の教科書には、もう部分分子容の加成則の身の置き所はなくなっているようにも見える。 加成則は今日、理学ではなくむしろ工学の分野において物性推算法として生き永らえているのが現状である。 しかし、銘記して置かねばならないことは、部分分子容の加成則をめぐる問題はあくまでも「忘れられた」のであって「乗り越えられた」のではない、ということである。 この節では簡単にその歴史的な展開を跡付けるとともに、それがもたらした知見を概観する。
これまで物理化学という学問の成立を、Z. Phys. Chem. の創刊された1887年に求める見解が有力であるが、 それに先立って1840年ころから物質の物理的性質と化学的性質のはざまを研究対象とする動きは始っている。 その中心的なテ-マとして化学量論の問題があり、分子容の加成則はその格好の材料となった。 この19世紀半ばからの体積の化学を支えた人物 H. Kopp (今日ではむしろ化学史家として知られているかもしれないが)の初期における分子容研究の集約ともいえる論文の表題が “Beiträge zur Stöchiometrie der physikalischen Eigenschaften chemischer Verbindungen” [5.1]であることはこの時期の化学者の志向を如実にもの語っているように思われる。 しかし、19世紀も後半に入るとようやく分子論が確立し議論の展開の視点にも変化が現われてくる。 こうした時、J. Traube による部分分子容の加成則に関する研究があらわれた[5.2]。 今日行なわれている部分分子容の加成則に関わる研究もその本質的な点においてこの Traube による研究を越えるものではない。 むしろ Traube の当時には知られていなかったさまざまな分子論的な物語をそこに投入した結果、混乱だけが増しているようにさえ思われる。
Traube のえた画期的な成果は、まず、ある溶媒中で溶質の示す部分分子容が等温・等圧条件下で加成則を満足することを見い出しそれを次のように表わしたことである。
\begin{equation} V = \mathit{\Phi} + \sum n_i v_i \label{eq:5.1.1} \end{equation}
ここで \(n_i\) は分子中に含まれる \(i\) という構成要素(Traube は原子を考えた)の数であり、\(v_i\) はその構成要素の部分分子容に対する寄与である。 第一項の \(\mathit{\Phi}\) は Traube 名付ける所の共通体積 Covolumen であり、普通の有機溶媒では 25 cm3 mol-1 程度の値をとる。 この共通体積に相当する項は最近の研究においても、部分分子容を分子各部の寄与に分割していく際に必要な量として取り入れられている。 たとえば寺沢らの扱い [5.3]ではファンデルワ-ルス体積 \(V_\mrm{W}\) を用いて部分分子容を
\begin{equation} V = a V_\mrm{W} + b \label{eq:5.1.2} \end{equation}
のように表わすわけだが、この第二項に\eqref{eq:5.1.1}式の \(\mathit{\Phi}\) に相当する項が含まれていることになる。
提唱者の Traube をはじめ多くの人びとによってこれまで多くの物質の部分分子容が測定されこの枠組に沿って解釈がなされた。 そして、入り組んだ構造(たとえば環状構造)を持つ物質については \eqref{eq:5.1.1} 式では不十分であることが明らかとなり、 それは \eqref{eq:5.1.1} 式に対する補正項としてこの枠組の中に組み込まれることになった。
この表式で興味深いのは共通体積という項である。 この項は、単純に \eqref{eq:5.1.1} 式を拡張すれば「何もないもの」の部分分子容に相当する。 これは、その当時の気体分子運動論とも結び付いて分子運動による体積として解釈された。 実際、\(\mathit{\Phi}\) の温度・圧力依存性はこの予想を裏付けるように、\(v_i\) の温度・圧力依存性よりも大きな値を示し、 またその大きさはファンデルワ-ルス方程式から予測されるようなオ-ダ-のものであった。[補注11]
Traube による部分分子容の加成則の発見とその展開には目覚ましいものがあった。 しかし、それに関わる彼のさまざまな見解は、今日的にみればいくつかの欠点を持っている。 まず、共通体積なるものについての解釈は明らかに誤りである。 すでに1章でみたように、部分分子容に対する並進運動の寄与は \(\kappa_T k_\mrm{B} T\) に等しい。 これは通常取扱われる液体ではせいぜい 5 cm3 mol-1 であり Traube によって見い出された、 約 25 cm3 mol-1 という \(\mathit{\Phi}\) の大きさをとうてい説明できるものではない。 共通体積なるものの起源は、もっと根深い所に求められねばならないはずである。 さらに、大きな問題として原子固有の体積へのあまりに強い思い入れがある。 これが彼をして共通体積に執着させることになったし、また原子の部分分子容に対する寄与 \(v_i\) をさらに原子のコアの体積と、 原子の運動による体積とに分割するような方向へ導いたように思われる。 彼の総説 [5.2] の題名、“Ueber den Raum der Atome” はその思いを伝えている。 すでに3章で詳しく述べたように、このような方向は巨視的なイメ-ジと微視的現象の安易な結合に落ちいく結果をもたらす。 彼の苦闘の様は、その後の体積変化の化学における多くの化学者の苦闘の様のようにも見える。
Kopp が最初に分子容の分子論を論じた時代には、分子論・化学量論それ自身が対象であった。 分子論がようやく確立する時代に生きた Traube にとってはおのずと問題の立て方は異なることになった。 彼は体積から分子を見るのではなく、分子から体積を見ようとした。 しかし、体積を分子の世界から見るには従来を越えた理解の枠組が必要とされる。 Traube の業績が今日忘れられることになったのは、それを十分に彼が与ええなかったことにあるといえよう。 そしてまたそれは今日においても与えられてはいないのである。 体積変化の化学の今日の状況はそのことを雄弁にもの語っている。 最後にもう一度「部分分子容の加成則は『忘れられた』のであり『乗り越えられた』のではない。」ことを強調して、このいささか長い加成則の研究の跡付けについての節を終えることにする。
まず部分分子容の加成則がどの程度成立するものかを検討してみることにしよう。 当然のことながら成立しない場合を指摘することはたやすい。 加成則からのはずれを指摘し、意味ありげにその加成則からのはずれに分子論的解釈を与えるというのはこれまでも多く行なわれていたところである。 しかし、問題は成立しない場合にあるのではなく、成立する場合にあるはずである。 ここでは、従来からよく成立するとされている、n-アルカンについてどのような条件下で加成則が成立するのかを検討する。
もし n-アルカンについて部分分子容の加成則が成立するならば、部分分子容 \(V\) は対象とするアルカン分子の炭素数を \(n\) として次のように書けるはずである。
\begin{equation} V = \alpha n + \beta \label{eq:5.2.1} \end{equation}
以下、部分分子容の加成則はこの式に基づいて検討するものとする。
図 5.1 に純アルカン液体の分子容について、1気圧さまざまな温度での加成則からのはずれをプロットした。 加成則はおおまかにはよく成立しているが低分子量のアルカンで加成則からの予測より、より大きな分子容が観測されている。 温度が高くなるにつれ、高分子量のアルカンも加成則から外れるようになる。 これは、沸点が観測する温度に近いものほど加成則からのはずれが大きいという形でまとめることができる。

|
図 5.1. 純 n-アルカン液体の分子容の加成則からのはずれ。 加成則からの計算値を得るのに用いた加成則の係数は、その温度で液体であるアルカンの内、 沸点のより低い 5 個のアルカン(図中の白抜きの点)を除いたものについて1次関数に最小二乗法でのせることにより得た。 用いた分子容の値は [5.4]による。 |
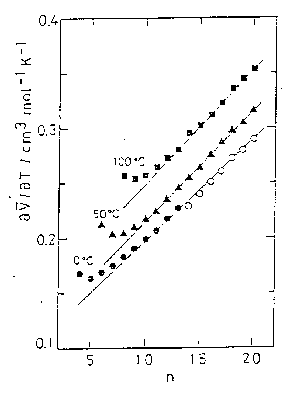
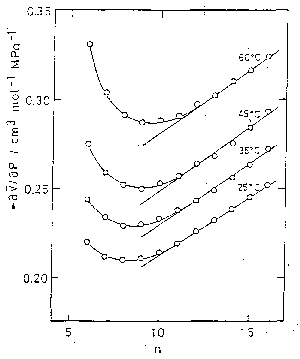
このはずれは、分子容の温度・圧力依存性についてみるとよりはっきりする。 もし、加成則が厳密に成立するならば分子容の温度・圧力微分についても加成則が成立しなければならない。 図 5.2、図 5.3 は、\(\partial V/\partial T\)、\(\partial V/\partial P\) を炭素数 \(n\) についてプロットしたものである。 分子容それ自身の加成則についてみられたようなはずれがより明瞭に現れてきている。 この純アルカン液体における加成則からのはずれは低級アルカンが比較する温度・圧力のもとでは気体であることを考えれば、十分予測されたことである。
|
|
| 図 5.2. 純 n-アルカンの分子容の温度微分に対する加成則の成立状況。 用いた分子容の温度依存性の値は [5.4]による。 | 図 5.3. 純 n-アルカンの分子容の圧力微分に対する加成則の成立状況 [5.5]。 |
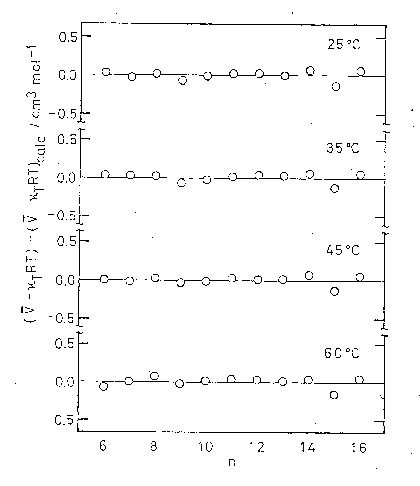
このような加成則からのはずれを1章でみた部分分子容の組立ての上から調べると興味深いことに、 はずれは配置の寄与ではなく並進の寄与からきていることがわかった。 図 5.4 に配置の寄与のみについて加成則 \eqref{eq:5.2.1}式をあてはめたときの偏差を示す。 図 5.1 で見られたようなはずれは消失し、実験誤差範囲内で加成則が成立していることがわかる。 このような部分分子容への配置の寄与についての加成則の成立が、液体状態のアルカンをはなれて、 検討している温度・圧力の下で気体であるようなアルカンにまでおよべばきわめて一般的な法則として加成則を定式化することができる。 しかし、気体状態のアルカンについてまではこのような配置の寄与の加成則の外挿はかなわない。 たとえば、エタンでは 30 ℃、1 atm で -370 cm3 mol-1 と液体の加成則からの予測値 61.7 cm3 mol-1 を大きく下回る結果を与える。 たしかに、純アルカンの分子容を部分分子容として捉えその配置の寄与に注目することによって、分子容そのものを対象とするよりはるかによく成立する加成則をえることができる。 しかし、それは液体状態のものについてのみ可能なようである。 臨界点以上の領域を経由することによって、液体から気体への移行は連続的に可能である。 この配置の寄与に対する加成則がそのような連続的変化にともないどのようにふるまうか興味あるところである。
|
図 5.4. 純 n-アルカンの分子容の配置の寄与に対する加成則の成立状況。 用いたデ-タは [5.5]による。 |
ある溶媒に一連のアルカンを溶かした溶液について、その溶液におけるアルカンの部分分子容について加成則の成立状況を調べた。 異なるアルカンについてその部分 分子容を比較するのだから、比較するときの濃度をいかに設定するか、モル分率がよいか、体積分率がよいか...が問題となる。 ここでは、多くの実験家によって濃度単位として採用されているという理由から、部分分子容に対する加成則の検討は同じモル分率で比較することにした。
|
図 5.5. シクロヘキサン中の n-アルカンの部分分子容に対する加成則のいくつかのモル分率 \(x\) における成立状況。 1 気圧。○、\(x = 1.0\); △、\(x = 0.5\); ●、\(x = 0\)。用いたデ-タは[5.6]による。 |
図 5.5 にシクロヘキサンを溶媒ととったとき、加成則の成立状況が比較する濃度によってどう変化するかを示した。 アルカン濃度が低くなれば低くなるほど加成則の成立状況はよくなり、無限希釈では実験誤差内で加成則の成立が確認された。 他の溶媒についてもこのことは見い出された。 いくつかの溶媒について決めた無限希釈条件下での係数 \(\alpha\)、\(\beta\) を表 5.1 に示す。
| 溶媒 | 温度/°C | \(\alpha\) | \(\beta\) | \(n\) a) | \(\sigma\) b) | 文献c) |
|---|---|---|---|---|---|---|
| シクロヘキサン | 25 | 16.62 | 32.9 | 6-16d) | 0.07 | [5.6] |
| シクロヘキサン | 40 | 16.70 | 35.0 | 6-16d) | 0.10 | [5.6] |
| 1-クロロナフタレン | 25 | 16.57 | 26.5 | 6-16e) | 0.14 | [5.7] |
| 四塩化炭素 | 25 | 16.53 | 33.4 | 5-10 | 0.3 | [5.8] |
| エタノ-ル | 25 | 16.51 | 34.6 | 5-10 | 0.5 | [5.9] |
| ベンゼン | 25 | 16.95 | 32.1 | 5-10 | 0.2 | [5.9] |
| 水 | 23 | 16 | 18 | 2-3 | - | [5.10] |
|
a)加成則の係数の決定に用いたアルカンの部分分子容のデ-タの範囲。 b)加成則からのはずれの標準偏差。 c)加成則の係数の決定に用いたデ-タの出典。 d) \(n\) = 6-12 と \(n\) = 16 のアルカンのデ-タ。 e) \(n\) = 6, 7, 8, 12, 15, 16 のアルカンのデ-タ。 |
||||||
このように、無限希釈条件で部分分子容の加成則がよく成立することが確認されたわけだが、 この条件下、比較する温度・圧力条件下では純粋なものが気体であるようなアルカンにまでも、加成則がおよぶことは驚くべきである。 表 5.2 に四塩化炭素、ベンゼン溶媒におけるメタン・エタンの無限希釈での部分分子容の実測値と、 炭素数 5 から 10 のアルカンの部分分子容に対する加成則からの外挿値を示した。 メタンについては実測値がより大きくなる傾向を持っているようだが、 エタンについて加成則からの予測値はほぼ実測値と一致する。
| 物質 | 四塩化炭素中 | ベンゼン中 | ||
|---|---|---|---|---|
| 実測a) | 計算b) | 実測a) | 計算b) | |
| メタン | 52.4 | 48.9 | 51.9 | 49.0 |
| エタン | 66.0 | 66.5 | 66.1 | 66.0 |
|
a)文献 [5.11]。 b)炭素数 5 から 10 のアルカンのデ-タから加成則を用いての計算値。 |
||||
このように、溶液にしたときには無限希釈で加成則がきわめてよく成立するようになることが明らかとなった。 これは、溶質-溶質の相関を無視できるような条件下で加成則はよく成立すること、つまり溶媒-溶質の相関を考える限りは加成則がよく成立するものであることを示している。 粒子数揺らぎの立場からいえば次のようになる。
\begin{equation} \frac{\langle \delta N_\mrm{S} \delta N_\mrm{X} \rangle}{\langle N_\mrm{X} \rangle} \propto n \label{eq:5.2.2} \end{equation}
どうも、理論的にはけっして自明なものとはいえないが、無限希釈の部分分子容に対する加成則は十分信頼するに足る法則(経験則)であると結論せざるをえない。 以下、これを前提にして分子のパッキングという視点から加成則で見えてくる部分分子容の挙動、特に係数 \(\alpha\) と \(\beta\) のふるまいを検討していく。
\eqref{eq:5.2.1} 式の係数 \(\alpha\) と \(\beta\) はかなり異なる挙動を示す。 一般に \(\alpha\) は \(\beta\) に比して、温度・圧力、あるいは溶媒に対して鈍感である。
巾広い温度・圧力領域で、 \(\alpha\) と \(\beta\) の温度・圧力依存性について検討する上で、 現時点では純アルカン液体に対する加成則からのデ-タを用いて議論するしかない。 しかし、純アルカン液体と溶媒中での部分分子容の挙動とはさほどことならないようなのでここでは、 純アルカン液体についての温度・圧力依存性のデ-タで全体の描像を描いてみることにする。
|
|
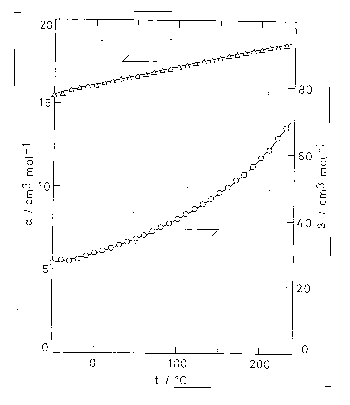
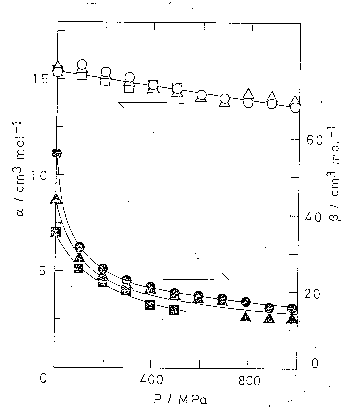
| 図 5.6. 純 n-アルカンの分子容の加成則の係数 \(\alpha\) と \(\beta\) の温度依存性。 1 気圧。用いたデ-タは[5.4]による。 | 図 5.7. 純 n-アルカンの分子容の加成則の係数 \(\alpha\) と \(\beta\) の圧力依存性。 用いたデ-タは[5.12]による。 |
図 5.6 には、\(\alpha\) と \(\beta\) の圧力 1 atm での温度依存性、図 5.7 には 0、50、100 °C における圧力依存性を示す。 圧力依存性について、200 Mpa までの範囲ならばもっと精度の高いデ-タが存在するが、ここでは圧力範囲を広くとるため少し精度が落ちるが Bridgman のデ-タ[5.12]を使用してある。 あきらかに \(\alpha\) に比して \(\beta\) の方が大きな依存性を示す。 たとえば、1 atm で 0 °C から 100 °C にまでしたときに \(\alpha\) は 16.1 cm3 mol-1 から 17.2 cm3 mol-1 まで、 約 7 % の増加を示すのに対し、 \(\beta\) は 30.1 cm3 mol-1 から 40.5 cm3 mol-1 まで約 30 % の増加をみる。 また圧力依存性についてみると 50 °C で常圧から 980 MPa にまでしたときに \(\alpha\) は 15.5 cm3 mol-1 から 13.9 cm3 mol-1 と約 10 % の減少を示すのに対し、 \(\beta\) は 43.4 cm3 mol-1 から 12.9 cm3 mol-1 と約 70 % の減少を示す。
このような \(\alpha\) と \(\beta\) の性格のちがいの分子論的な意味は後で論じるとして、 この\(\alpha\) と \(\beta\) の圧力依存性のちがいはアルカンの PVT 性質についての興味深い現象と結び付いている。 アルカンの等温圧縮率について加成則を前提にすれば
\begin{eqnarray} \kappa_T &=& -\frac{1}{\alpha n + \beta} \pdif{(\alpha n + \beta)}{P} \nonumber \\ &=& -\frac{1}{\alpha n + \beta} \left[\pdif{\alpha}{P} n + \pdif{\beta}{P} \right ] \label{eq:5.3.1} \end{eqnarray}
となる。 圧力をかけるに従って \(\beta\) が急速にその寄与を減じていけば、この値は \(n\) によらなくなり、 \(-(1/\alpha)(\partial \alpha/\partial P)\) に接近する。 つまり、高圧下では圧縮率はアルカンの種類によらなくなるのである。 これは、さまざまな液体について Bridgman が実験的に示したところである[5.12]。
ここまで、純アルカン液体の挙動をみてきたわけであるが、無限希釈における部分分子容からえられる \(\alpha\) と \(\beta\) についてみると、 溶媒依存性の問題がある。 この溶媒依存性についてみても、\(\alpha\) の方が \(\beta\) に比して鈍感である。 表 5.1 のと \(\alpha\) の値は、16 cm3 mol-1 から 17.0 cm3 mol-1 までとその変動は約 7 % の巾におさまるのに対し、 \(\beta\) は 18 cm3 mol-1 から 35 cm3 mol-1、 水の値は実験点がわずか2点なので除くとしても、 26.5 cm3 mol-1 から 35 cm3 mol-1 と、 20 % から 30 % の巾で変化している。
このように \(\beta\) の値が大きく変化することは Traube の見い出した"共通体積"についての挙動に対応するものである。