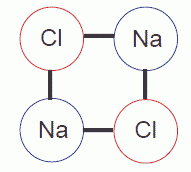
| 図 A.1 2個ずつの Na 原子と Cl 原子で作られる1辺の長さ r の正方形型の原子配置。 Na-Cl の対は4個存在する。 |
物質不滅の法則に基づく化学量論の要請を認めることで、 線形空間が形作られ、 化学種と称されるベクトルが多彩な化学反応の世界を作りました。 しかし果たしてこうした取り扱いは絶対なのでしょうか?
たとえば次の反応方程式を見てください。
Na + Cl → NaCl (A.1a)
Na + Cl → 2NaCl (A.1b)
(A.1a) 式はだれも依存の無いところでしょう。 それでは(A.1b) 式は? 中学、高校、あるいは大学でも、テストでこんな式を書いたら、 「係数が釣り合っていない」 というので、ただちに×でしょう。
でも本当にそうでしょうか? NaCl 分子を仮に「原子間の距離が r 近傍のNa 原子と Cl 原子の対」と定義したとしましょう。 もしこの定義に立つならば、図 A.1 の場合、2個のNa 原子と2個の Cl 原子から、4個の NaCl 分子ができています!
2Na + 2Cl → 4NaCl (A.2)

| 図 A.1 2個ずつの Na 原子と Cl 原子で作られる1辺の長さ r の正方形型の原子配置。 Na-Cl の対は4個存在する。 |
(A.1b) 式はまちがっていません! さらに言うなら食塩の結晶の中で、格子定数の半分の距離にある NaCl の対を「NaCl 分子」とみなすと、
Na + Cl → 3NaCl (A.3)
という反応方程式が成立します!
|
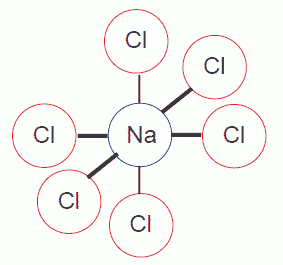
図 A.2 面心立方型の NaCl 結晶中の Na 原子とそれと隣接する6個の Cl 原子。
Na-Cl の対は1個の Na 原子あたり3個存在する。 |
こうした化学反応方程式の綻びは、通常、次のようにして繕われています。 たとえば(A.1b) 式であれば、(A.2) 式の形にして、次のように書きなおすのです:
2Na + 2Cl → Na2Cl2 (A.1b')
あるいは
2Na + 2Cl → (NaCl)2 (A.1b'')
つまり分子の定義を変更して 「これは NaCl ではなくて Na2Cl2 だった」 あるいは 「これは NaCl ではなくて NaCl の二量体だった」 ということにするわけです。 あるいは「食塩の結晶の場合には、化学式は分子式ではなく組成式で示す」 という表現なども教科書でおなじみでしょう。 これは (A.3) 式を次のように書き
m Na + m Cl → NamClm (A.3')
m が極めて大きいとして、(1/m) NamClm を NaCl と略記したことに相当しています。
ここでの話のポイントは、 「何が分子かは、人間が定義する」 という何でもないようですが、重要な事実です。 かつてこのことに気づいた時、ぼくは「これぞコペルニクス的転回だ」と感動したものでした。 ぼくたちは化学量論を満たすように分子・化学種を定義することで、 線形空間を構成します。 こうした化学種の定義の仕方は、 特に質量に関する量的な関係を議論する上で有用です。 しかし場合によっては、そうした化学種の構成法を捨てた方が、よりよくものごとを理解できるかもしれません。 たとえば食塩水中に、Na+、Cl- 以外に、NaCl、NaCl2-、Na2Cl+、 Na2Cl2、・・・・といった無数の分子種を想定することは可能です。 けれども当面の説明のために次々とこうした分子種を動員し、 そこに化学量論からの要請を課した時、そうした分子種に足を取られて事態を見誤る恐れは大きいでしょう。