３．塩化クロムの加水分解にともなうスペクトル変化

市販の塩化クロム(III)六水塩は[CrCl₂(H₂O)₄]Cl・2H₂O に相当する化学式を持ち、 希薄な水溶液中で

[CrCl₂(H₂O)₄]⁺ → [CrCl (H₂O)₅]²⁺ → [Cr (H₂O)₆]³⁺

と逐次加水分解を起こし、緑色の溶液が紫色に変色することが知られています。

写真 3-1. 固体の塩化クロム(III)六水塩を水に溶解直後。	写真 3-2. 溶解後、一晩おいた後の溶液。

この実験はきわめて簡単。 光学セルに水を2～3 mL程度入れ、 塩化クロム(III)六水塩を 10 mg 程度（スパチュラの先に少し乗るほど）加えて撹拌し溶解（スポイトで水を加え、何度か吸入・吐出を繰り返せばよい）、 ただちにスペクトルの時間変化をとればよいのです。 塩化クロム(III)は潮解性なので、手早く操作します。

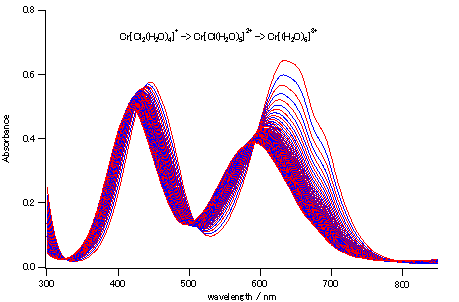
図 3-1. 塩化クロム(III)六水塩の加水分解にともなうスペクトル変化。 1分間隔でのスペクトルを取った結果。 室温27°C。

図 3-1 は７月に行った実験結果で、CHEMUSB 4を用いスペクトル変化を１分おきに測定した結果です。 1分間隔でデータの格納を行っています。２つの反応が関与するので、等吸収点は生じません。 なおこの実験を冬場に行い、室温が20℃を切るようだと、反応に倍以上の時間がかかり、学生実験の時間中に行うのは現実的ではありません。 この反応に限らず、CHEMUSB 4を用いた反応速度の実験では温度制御が大きな問題となります。 季節にもよるのですが学生実験の時間の室温の変動はたいてい2℃程度で収まるので、室温で起きる反応の反応速度則には、実験精度を考えるとあまり大きな影響はでません。 しかしたとえば同じ25℃で比較したい、速度定数の温度依存性を調べたいという時には、温度制御は避けて通れません。 1 cm角の光学セル組み込めるサイズの恒温ユニットがあればよいのですが・・・。

吸光度の時間変化は次のように反応速度則を組み合わせることで得られます。 クロム(III)のジクロロ錯体CR2（[CrCl₂(H₂O)₄]⁺）が、 逐次、モノクロロ錯体CR1（[CrCl (H₂O)₅]²⁺）、 アコ錯体CR0（ [Cr (H₂O)₆]³⁺）と解離する反応の、 単位体積当たりの反応進行度をそれぞれy₁、y₂とします：

CR2 → CR1 + Cl^-　　y₁　　(3-1a)
CR1 → CR0 + Cl^-　　y₂　　(3-1b)

それぞれの反応速度が１次の速度則に従うものとすると、c₀をジクロロ錯体の初濃度として、次の方程式が成立します：

d y₁/dt = k₁ [CR2] = k₁ (c₀ - y₁)　　(3-2a)
d y₂/dt = k₂ [CR1] = k₂ (y₁ - y₂)　　(3-2b)

この連立微分方程式を解くと次式が得られます^*1。

y₁ = c₀ [1 - exp(k₁t)]　　(3-3a)
y₂ = c₀ [1 + (k₂/(k₁ - k₂)) exp(-k₁t) - (k₁/(k₁ - k₂)) exp(-k₂t)]　　(3-3b)

一方塩化クロム溶液の吸光度は、ランベルト-ベールの法則から、単位体積当たりの反応進行度y₁、 y₂を用いて次式であらわすことができます。

A = ε_CR2 [CR2] + ε_CR1 [CR1] + ε_CR0 [CR0]
　= ε_CR2 (c₀ - y₁) + ε_CR1 (y₁ - y₂) + ε_CR0 y₂
　= ε_CR2 c₀ + (-ε_CR2 + ε_CR1) y₁ + (-ε_CR1 + ε_CR0) y₂
　= A₀ + a₁ y₁ + a₂ y₂ 　　　(3-4)

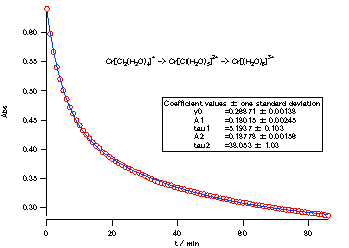
図 3-2. 塩化クロム(III)六水塩の加水分解にともなう630 nmの吸光度の時間変化と、 それを２つの指数関数の和で当てはめた結果。 室温27°C。

ここで光路長を1とおきました。 またA₀は加水分解が始まる前の吸光度、a₁、a₂は、吸光係数で決まる定数です。 反応進行度が、(3-3)式で与えられますから、 吸光度変化は異なる時定数を持つ２つの指数関数の和（double exponential function）で表わされるわけです。 このことは実際に得られた630 nm の吸光度の時間変化に、最小２乗法で関数の当てはめを行うことで確認することができます。 この日の水温はおよそ27 ℃でしたが、初段の速度定数は 0.19 min^-1、最終段の速度定数は 0.026 min^-1 ということになります。

単色化した光を用いて強度の測定をしていた以前の装置では、 紫外・可視域のスペクトルを取るのに時間がかかり、1分ごとの吸光度の時間変化を追うのには、波長を固定するのが当たり前でした。 こうしたある波長における吸光度変化（時間スキャン、タイムコースなどと呼ばれるもの）は、 CHEMUSB 4では、一定時間おきに取り込んだスペクトルを、ある波長領域で切り取ったものに相当し、ストリップチャートと呼ばれます。 スペクトルを取るのに1秒かからないわけですから、 時間分解能が1分程度なら、波長を固定する必要はないという見方もできます。 けれども反応速度を検討する上で実際上必要とされるのは、変化の大きな波長での吸光度だけです。 データを最初から切り捨てることで、 データ処理にかかる労力を省くことがでます。

たとえば２時間にわたって１分おきにスペクトルデータ蓄積すると、 CHEMUSB 4で取得される１つのスペクトルデータは50 kB程度のサイズがあり、 全部で6 MB程度のデータを扱うことになります。 もし解析に利用するのが630 nmの波長の吸光度のデータだけであれば、 実際に使用されるのはほんの数kBにすぎません。 最初から注目する波長に限って、吸光度の時間変化を得る方が、後のデータ処理の負担が軽く有利といえます。 せっかくのデータを捨ててしまうことになるわけですが、 場合によってはその方が、効率的に事態の本質にたどり着ける場合もあることに、注意してもらってよいでしょう。

表紙に返る