last revised 2020.11 / 2020.10
吉村洋介
0.物理化学・物性化学実験の準備
III. 気体の粘度
<概要>
気体の粘度に関して気体分子運動論から導かれる重要な性質として次の3点が挙げられる:
- 気体の粘度は圧力によらず一定である。
- 温度が高くなると気体の粘度は大きくなる。
- 分子間相互作用が大きくなると気体の粘度は小さくなる。
こうした特性は日常目にする液体の粘度とは大きく異なり、J. C. Maxwellが理論の予見(1860年)の通り、
実験的に気体の粘度が圧力によらず一定で、温度が高いほど大きいことを示した(1866年)ことは初期の気体運動論の大きな成功であった。
今回の実験ではこの3つの特性の内、(1)と(3)に注目する。
操作
減圧した容器にガラス管に詰めた綿を通して気体(空気、ブタン)を流入させ、
その際の容器の圧力の時間変化がどのような法則に従うかを確認し、
気体の種類による粘度のちがいを知る。
ブタンを用いるときは着火しないよう十分注意を払うこと。
- 長さ約12 cmの外径4 mmのガラス管(内径2.4 mm)に脱脂綿を詰める。
およそ8 cm程度の長さにわたって綿が均一に詰まるようにする(以下「流通管」と呼ぶ)。
- 500 mLのナス型フラスコに(1)で作った流通管を取り付ける。
- フラスコをダイアフラムポンプで吸引し減圧する。
- 10 kPa 程度まで圧力が下がったら、ダイアフラムポンプとフラスコを結ぶチューブをピンチコックで閉じ、
数分待って圧漏れがないことを確認する。
- 圧漏れがないことが確認できたら流通管とフラスコを結ぶチューブを開き、
圧力の時間変化を5~15秒程度間隔(変化の程度に応じて調節する)で測定する。
- 内外の圧力差が2 kPa程度になるまで測定を続ける。実験は2回行って再現性を確認する。
解析して得られる \eqref{eq:III-3} 式の \(k\) の値が10%以内で一致しない時は、
流通管の綿の詰まり具合などもチェックして実験をやり直す。
- <火気厳禁!>空気について実験を終えたら、ポリ袋にカセットコンロ用燃料(ブタン)を詰めて、
同様に気体をフラスコに導入する実験を行う。余裕があればガスダスター(主成分ジメチルエーテル)を用いてもよい。
- 【余裕があれば】流通管を60 °C程度に保った湯につけ、空気の粘度の温度依存性を調べてみよ。
<結果の解析>
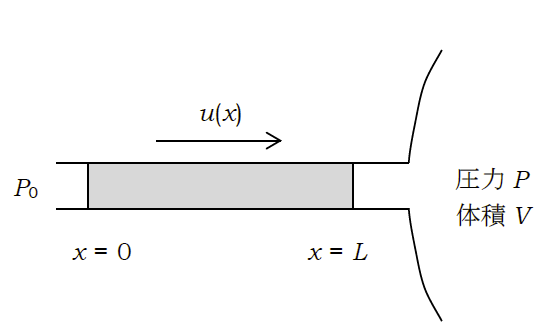
図 1 のように、大気圧 \(P_0\) の状態にある気体が、長さ \(L\) にわたって均一に綿を詰められた流通管を介して、
圧力 \(P\)、体積 \(V\) のフラスコに流入する状況を考える。
圧力の勾配は実質的に綿の層にのみ存在し、綿を詰めた部分の端から距離 \(x\) における気体の流量 \(u(x)\)(単位時間当たり流れる体積)
が圧力勾配に比例するものとする:
\begin{equation}
u(x) = -G \frac{\rmd P(x)}{\rmd x}
\label{eq:III-1}
\end{equation}
ここで \(G\) は比例定数で、気体の粘度に反比例すると考えることができる。
気体の粘度が圧力に依存しないなら、\(G\) は \(x\) によらず一定と見なせるはずである。
今回の実験条件では、気体の流れは定常状態にあるものと考えることができる。
定常状態では、粒子数の流れ(流量に数密度 \(\rho(x)\) を掛けたもの)は場所によらず一定 \(c\) であるとみなせる:
\begin{equation}
c = \rho(x) u(x) = - \rho(x) G \frac{\rmd P(x)}{\rmd x}
\label{eq:III-2}
\end{equation}
室温を \(T\) とすれば、状態方程式から \(\rho(x) k_{\mathrm{B}} T = P(x)\) であるので
(\(k_{\mathrm{B}}\) はボルツマン定数)、
容器の圧力変化は流通管の綿を詰めた部分の長さを \(L\)、大気圧を \(P_0\) とすると次式で与えられる:
\begin{equation}
\frac{\rmd P}{\rmd t} = \frac{k_{\mathrm{B}} T}{V} c
= \frac{G}{2VT} (P_{0}^{2} - P^2) = k (P_{0}^{2} - P^2)
\label{eq:III-3}
\end{equation}
ここで \(G/2VL\) を \(k\) と置いた。
これを積分すると下式が得られる:
\begin{equation}
\ln \frac{P_0 - P}{P_0 + P} = - 2 P_0 kt + const
\label{eq:III-4}
\end{equation}
圧力 \(P\) について解くと次式となる(\(a\) は定数):
\begin{equation}
P = \left( \frac{2}{1 + a \exp(-2 P_0 kt)} - 1 \right) P_0
\label{eq:III-5}
\end{equation}
<検討課題>
- \eqref{eq:III-2} 式から \eqref{eq:III-3}、\eqref{eq:III-4} 式が得られることを教員にも分かるように示せ。
- 気体の粘度が圧力に比例するとしよう。
すると \eqref{eq:III-1} 式の比例定数 \(G\) は圧力に反比例し、\eqref{eq:III-4} 式は、\(G = G’/P\)とすると
\begin{equation}
\ln (P_0 - P) = -k' t + const
\label{eq:III-6}
\end{equation}
のようになることを示せ。\(k'\) は定数。
- 空気についての測定値を用いて、\(\ln [(P_0 - P)/ (P_0 + P)]\) 及び \(\ln(P_0 - P)\) を時間に対してプロットし、
どちらの関数に圧力変化がよく当てはまるか調べよ。
- (3)のプロットの直線の勾配から \(k\)(あるいは \(G\))の値を求めよ。
- 実験データを \eqref{eq:III-5} 式に当てはめて解析して \(k\) を求め、
(3)のプロットから得た \(k\) の値と比較せよ。
また \(k\)(あるいは \(G\))が気体の粘度に反比例するものとして、
空気とカセットコンロ用燃料の粘度の比を決め、
ブタンの文献値(資料編V-9参照)と比較せよ。
- 室温20 °C の時、流通管の温度だけを 60 °Cに上げて実験したとしよう。
もし粘度が温度によって変化しないなら、\(k\)の値は何倍になるか?
気体の粘度のこと
ここで取り上げる実験は随分以前に、
ステンレスのキャピラリーチューブを使用して行っていたものを、
簡易化したものです。
以前は水銀マノメーターだったのを、
簡易なデジタル圧力計に切り替え、
ガラス管に詰め込んだ綿を通じて流入してくる気体の流量をモニターするようにしています。
使用する気体は空気とブタン。
ブタンはカセットコンロ用のカセットボンベのブタンをポリエチ袋に吹き込んだものを使います
(火気厳禁!)。
最近は他にエアダスターも置いておいて、
ジメチルエーテルなども測ってみて良しということにしています。
実験は2人組で行い、
実験結果を解析、グラフ等を作成、
用意してあるレポートシートに記入、
提出して課題完了という流れです。
実験装置
実験装置は極めて簡単。
装置と呼ぶのも気恥ずかしいようなもので、
図 1a の写真のような構成で十分測定できます。
今回程度の真空度の実験だと、ガラスの摺りの部分にグリースを塗っておく程度で、
圧漏れ対策はたいてい大丈夫です。
注意すべきは水滴が付いていないことのチェックくらいでしょうか(特にゴム管の内部)。
この装置ですが、
取りあえず必要な資材は置いておいて、
めいめいで思い通りに作ってもらえばよいことにしています。
ちょっと考えると図 1a の構成だと実験できないように見えます。
そもそもどうやって減圧すればいいのでしょう?
減圧するにはフラスコとポンプをつなぐラインが必要で、
減圧中は流通管との間を閉じておかないといけません。
また減圧を終わったらポンプとのラインを閉じ、
流通管との間を開くことになります。
どうしたところでコックは2カ所は必要。
できれば圧力計との間にもコックが欲しいし、
一件をつなぐゴム管なども必要・・・
考え出すとどんどん装置は膨れ上がっていきます。
そしてパーツが増えていくごとに、
圧漏れが起きたりトラブルの種を抱え込むことになります。
図 1a の装置では、
あまり難しく考えず ”実践的” な手法で減圧すればよいのです。
例えば流通管の部分を一端外してポンプにつなぎ減圧します。
減圧が終わったら、
コックなど使わずとも、
ゴム管を手で折って押さえれば圧力は十分止まります。
そしてその状態でポンプから外して、
しばらく圧力の変動を見て圧漏れがないことを確認。
流通管を取り付け、
おもむろにゴム管を押さえている手を緩めて、
流通管からの気体の流入を起こして、圧力変化の測定をすればよいのです。
測定にあたっての注意点は、使用しているデジタル圧力計(コパル電子 PG-100)が3分ぐらいでオートオフがかかるので、
すぐにボタンを押して復帰させることぐらいでしょうか。

|

|
|
|
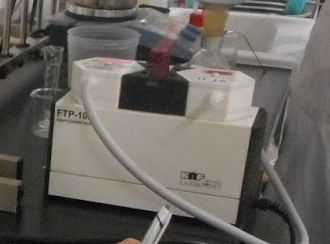
図 1a. 圧漏れ測定用の装置。
500 mL のナスフラスコに、流通管とデジタル圧力計(マノメータ)を付けたもの。
使っている圧力計は減圧蒸留の際にも使用した、
コパル電子(現日本電産コパル電子)のハンディ・マノメータ PG-100
(絶対圧型)。
|
図 1b. 流通管。外径 4 mmのガラス管(内径2.4 mm)に脱脂綿を詰めて作る。
詰め方がきついと時間がかかり過ぎるし、
緩すぎると粘性流の条件を満たさない。
|
図 1c. 減圧用のポンプ。
減圧蒸留で使用したもの。
普通に 2 kPa までは減圧可。調子がよければ 1 kPa を切るぐらいまでいける。
|
実験結果
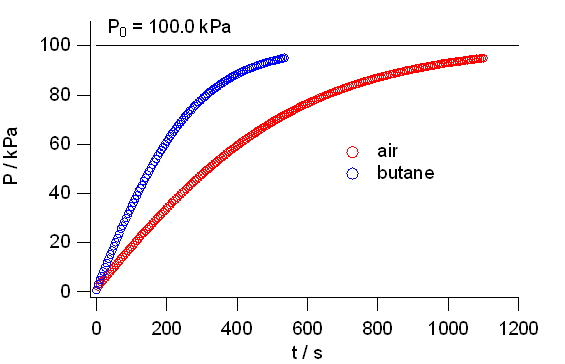
図 2 に実際の測定例を示します
(測定時間間隔を 5 秒に取っています。
気体の流通速度はもう少し遅い方がよいでしょう)。
ブタンの方が空気に比べて流入速度が大きいことが分かります。
密度はブタンが空気の2倍(空気の平均分子量 29 に対し、ブタン C4H10 の分子量 58)で、
ベルヌーイの式 \(v^2 /2 + P/ \rho = \mrm{const}\) からは、
同じ圧力差ならブタンの方が流入速度が小さいはずですが、
粘度が支配的にふるまう粘性流では事態は単純ではありません。
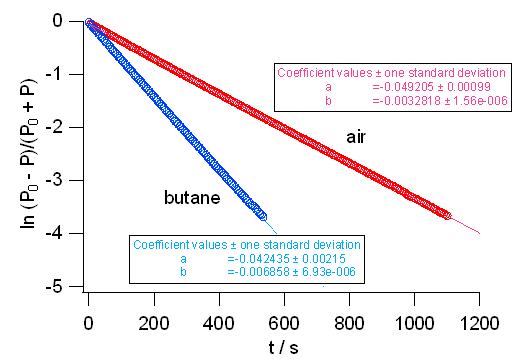
図 2b には式\eqref{eq:III-4} の成立状況を調べた結果を示します。
\(\ln (P_0 - P)/(P_0 + P) \) は時間に対し直線的に減少し、
式\eqref{eq:III-1} の粘度が圧力によらないという仮定が妥当なものであったことを裏付けています。
またブタンの直線の勾配は、単純に線形最小2乗法を適用すると空気の勾配の 2.1 倍になっていて、
300 K の粘度の文献値(ブタン7.5 µPs s、空気18.5 µPs s)から予想される 2.5 とだいたい合っていますが、
2割程度小さくなっています。
これには用いたブタンに空気が混入した可能性と、
流速が速すぎて粘性流としての扱いが少し破れた可能性が考えられます。
|
|
|
図 2a. 流通管を通じた気体の流入による圧力変化。
|
図 2b. 式\eqref{eq:III-4} の直線関係の成立状況。
|
非線形最小2乗法の利用
今回の実験で用いた圧力計、コパル電子の PG-100 のカタログによると、
精度は非線形性 ±0.5 % と ±0.2 kPa の大きい方ということになっています。
最小2乗法を適用する際には(”実践的”にはしばしば無視されますが)、
それぞれのデータ点の重み(分散の逆数に比例)を評価する必要があります。
圧力計の非線形性の誤差に目をつぶって、全領域で±0.2 kPa 程度の一定の不確かさを想定すると、
先の式\eqref{eq:III-4} の場合には、左辺の値の分散\(\sigma_y^2 \)は
誤差の伝搬則を用いて
\begin{equation}
\sigma_y^2 \approx \frac{4 P_0^2}{(P_0^2 - P^2)^2} \sigma_P^2 = \frac{4}{[1 - (P/P_0)^2]^2} (\sigma_P/P_0)^2
\label{eq:yvar}
\end{equation}
ですから式\eqref{eq:III-4} への最小2乗法による当てはめを行う際、
\(P_0 \sim 100~\mrm{kPa}\) なので、
単純に考えると 30 kPa 付近のデータ点の方が、70 kPa 付近のデータ点の3倍以上の重みをもっている
(30 kPa で1回測ることは、70 kPa で3回測ることに相当)ことになります。
専門的な科学技術用の描画ソフト(無論 Igor も)には、
こうした重みを付して最小2乗法を適用できるオプションがあります。
けれども式\eqref{eq:yvar} のような誤差の伝搬則を用いたりして測定点の重みを評価して直線への当てはめを考えるより、
重みをすべて一定として処理できた方が簡単でしょう。
こうした立場からは、課題にあるように非線形の最小2乗法の適用が考えられます。
図3に非線形の最小2乗法で、実験結果を式\eqref{eq:III-5} に当てはめた結果を示します。
当てはめは非常によく、
得られた \(k\) の値は空気について 1.65 × 10-5 kPa-1 s-1、
ブタンについて 3.47 × 10-5 kPa-1 s-1でした。
これは図 2b のプロットの傾き(\(= 2 P_0 k\))から得られる、1.64 × 10-5 kPa-1 s-1、
3.43 × 10-5 kPa-1 s-1 より若干(1 %程度)大きめになっていますが、
ほぼ一致しています。
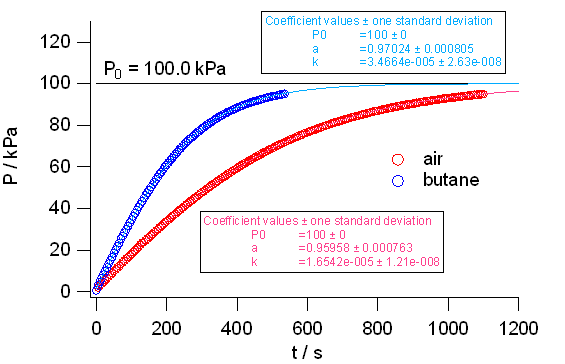
図 3. 非線形最小2乗法を用いた、式\eqref{eq:III-5} への当てはめ結果。
図 2b の式\eqref{eq:III-4} への当てはめがうまくいっているので、
等価な式\eqref{eq:III-5} への当てはめもうまくいっているのは当然でしょう。
しかし測定を長時間行って、\(P_0 - P\) が測定誤差に埋もれてしまうような領域までくると
\(\ln (P_0 - P)/(P_0 + P) \) は大きく変動し(\(P_0 - P \lt 0\) になれば値を持たない)、
式\eqref{eq:III-4} への当てはめは成功しません。
このような判断が必要ない点からも、
今日的には式\eqref{eq:III-5} を用いた非線形の最小2乗法が好まれることが多いようです。
なお線形の最小2乗法とちがって、
非線形の最小2乗法ではパラメーターの初期値の推定・設定といった問題があり、
しばしば「極小2乗法」になるので注意が肝要です。
生兵法は怪我の元ですので、
この機会に非線形の最小2乗法、
あるいはそもそもの最小2乗法について、
理解を深めておいてもらえることを期待します。
仮説の検証
検討課題の2では、
粘度が圧力に比例すると考えた場合の挙動と実験結果の比較検討を取り上げています。
粘度が一定ではなく圧力に比例するとしたら、
予想される圧力変化の挙動には大きな差異が生じると思われるかもしれません。
実際に粘度が圧力に比例するとして導かれる式\eqref{eq:III-6}、
\(\ln (P_0 - P) = -k' t + const\)
(ここで\(k' = G'/VL\))の左辺を時間に対してプロットしてみると、
図 4a に見るように、
遠目にはほとんど直線に乗っているように見えるでしょう。
けれどもよく見ると、
少し弧を描いていて、上に凸になっているのが分かります。
この点、粘度一定として導かれる式\eqref{eq:III-4} の左辺の値には、
そうした直線からの外れ・偏倚は見当たりません。
これをはっきりさせるためには、
最小2乗法で得た直線から実験値がどれだけ外れているか、
残差を示した図 4b を見てみれば明瞭です。
粘度が圧力に比例するとして場合の式\eqref{eq:III-6} の左辺の時間に対する勾配は、
空気の流入とともにより小さくなっていきます(勾配はより急になる)。
一方粘度が圧力によらないとした場合の式\eqref{eq:III-4} では、
勾配にほぼ変化はありません。
ただし初期に若干外れている様子が見受けられ、
温度の不安定性あるいは粘性流としての扱いの破綻などが現れているのかもしれません。
|
|
|
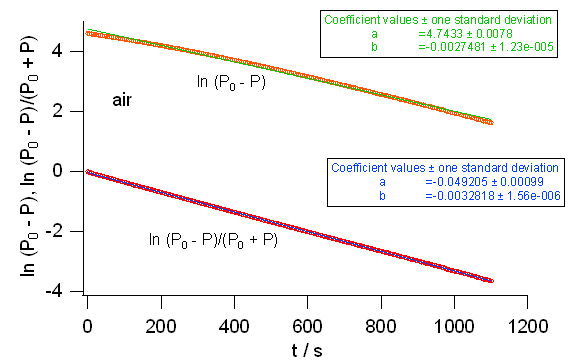
図 4a. 粘度が一定とした場合の式\eqref{eq:III-4} と
粘度が圧力に比例するとした場合の式\eqref{eq:III-6} の当てはめ(\(y = a + bt\) を使用)の状況。
式\eqref{eq:III-6} については実験値が、若干、直線から外れているのが見て取れる。
|
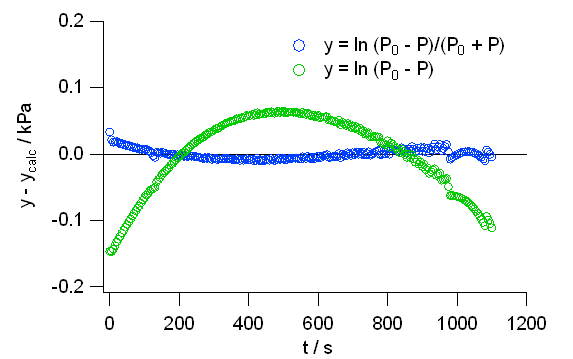
図 4b. 式\eqref{eq:III-4} と式\eqref{eq:III-6} へ当てはめた場合の計算値と実験値の偏倚(残差)。
粘度が圧力に比例するとした場合の式\eqref{eq:III-6} の偏倚が明瞭。
|
同様の比較を非線形最小2乗法の場合に行ってみたのが、図5 です。
比較対象が実測した圧力で、そのまま重ねて描いてみた図 5a. では曲線同士の比較になって、
先の図 4a. の直線からの外れを見るより少し見にくいですが、
残差を比較してみた図 5b では、
粘度が圧力に比例するとして場合の式\eqref{eq:III-6} から得られる
\begin{equation}
P = P_0 - A \exp(-k' t)
\label{eq:III-7}
\end{equation}
からの残差が、
初期の挙動に顕著に見て取れ、
低圧側で流入速度を過大に評価していることがわかります。
Igor には当てはめに \(y = y_0 + A \exp[(x - x_0)/\tau]\) という関数(exp_XOffset 関数)が用意されているので、
これを利用すればよいでしょう。
ここで扱う式\eqref{eq:III-7} にちょうど相当する \(y = y_0 + A \exp(kx) \) という関数(exp 関数)も用意されていますが、
使用は推奨されていません(以前のバージョンとの互換性維持のため残されている)。
これは長時間にわたる測定の中の、ある一部分を当てはめたいとき、
\(x\) をずらさないと(オフセットをかけないと)、
指数関数の引数に非常に大きな数が入る形になって、
計算が不安定になるためです。
また \(\tau\) で割る形になっているのは、
実際に使われる場面では、
速度定数ではなく時定数(平均寿命)で議論されることが多いためのようです。
一方、粘度が一定として場合の式\eqref{eq:III-5} の残差はわずかです。
ただし対数で表現した式\eqref{eq:III-4} でも見られましたが、
初期において、若干、負の値を取り、
最初の流入量を過少に評価しているようです。
このように特に非線形最小2乗法の場合には、
比較の際に残差を提示した方が当てはめの状況を把握しやすく、
また実際の測定値との比較なので、
偏倚の状況を想定しやすいメリットがあります。
ですから当てはめのよさを示すため、
残差を一緒に表示することが多く、
Igor などではそうしたオプションが付いているので、
機会があれば利用してみるのもいいでしょう。
|
|
|
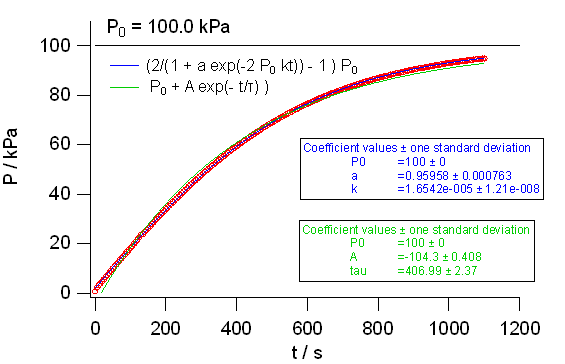
図 5a. 粘度が一定とした場合の式\eqref{eq:III-5} と
粘度が圧力に比例するとした場合の式\eqref{eq:III-7}(Igor 組み込みの関数 exp_XOffset で当てはめ)の当てはめの状況。
|
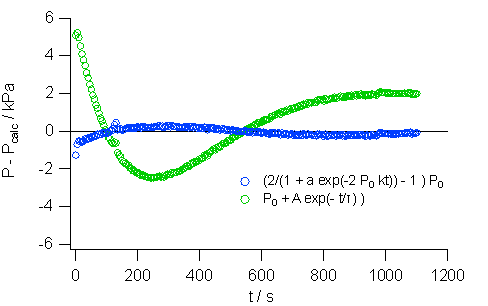
図 5b. 式\eqref{eq:III-5} と式\eqref{eq:III-7} へ当てはめた場合の計算値と実験値の偏倚。
粘度が圧力に比例するとした場合の式\eqref{eq:III-7} の偏倚が明瞭。
|
さてここまでは測定領域全体を取り上げてデータの当てはめを行い、
仮説の当否を見るという形の比較を行いました。
こうした比較を行うと、
いわば仮定した関係式の全領域にわたる偏倚の平均を扱うことになって、
偏倚が見えにくくなります。
こういう立場からは、
測定領域の一部分(たとえば測定結果の前半部分)について当てはめを行い、
そこから他の部分(測定結果の後半部分)の挙動を推定して、
仮定の当否を見るという方法が考えられます。
実際に線形最小2乗法、非線形最小2乗法について、
こうした比較を行った結果を図6 に示します。
局所的に行った最適化が、
大域的にどこまで通用するかを見るもので、
かなり厳しいチェックと言えるでしょう。
粘度が圧力に比例するという仮定が、
領域を拡張した時に破れることは一見して明らかでしょう。
|
|
|
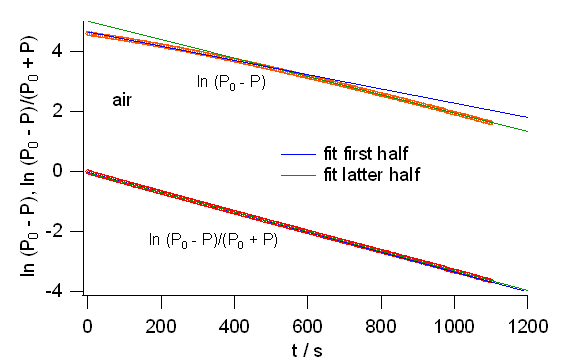
図 6a. 前半 0 ~550 s のデータと後半 550 s ~ 1100 s のデータ、それぞれを粘度が一定とした場合の式\eqref{eq:III-4} と
粘度が圧力に比例するとした場合の式\eqref{eq:III-6} に当てはめ、
それぞれの直線を後半・前半まで延長して示した結果。
粘度が圧力に比例するとした場合には、
延長すると重ならず、折れ線のようになる。
|
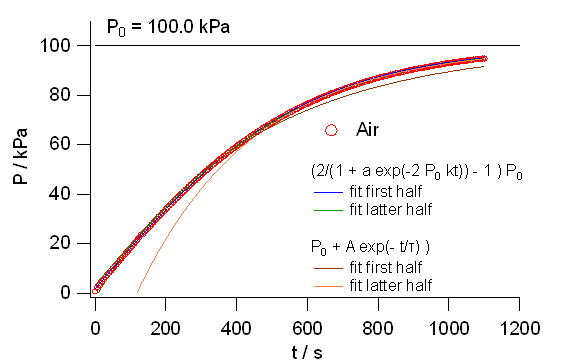
図 6b. 前半と後半のデータを、それぞれ粘度が一定とした場合の式\eqref{eq:III-5} と
粘度が圧力に比例するとした場合の式\eqref{eq:III-7} に当てはめ、
後半・前半まで延長して示した結果。
粘度が一定であるとした式は、領域外への外挿に耐えるが、
粘度が圧力に比例するとした場合には、
外挿すると実験データから大幅に外れる。
|
このような比較検討は、反応速度の実験などではよく見られるところです。
たとえば A → B という反応の速度則を検討する場合、
A の初濃度を変化させて反応の初速度を測定し、
その濃度依存性から反応の次数を決定するという手法は、
ここでの手法に通じるものがあると言えるでしょう。
たとえば気相でのアセトアルデヒドの熱分解反応
CH3CHO → CH4 + CO
の反応速度はアセトアルデヒド濃度の 3/2 乗に比例することが知られていますが、
アセトアルデヒド濃度の経時変化(圧力変化)を見ているだけでは、
反応次数の決定はなかなか難しいのです
(この反応はメチルラジカルの関与する連鎖機構で進行し、
連鎖の停止がもっぱらメチルラジカルの再結合で起きるというシナリオが流布されています)。
気体の粘度のはなし
この実験は2007年度から始まった後期実験の見直しの中で、
最初は「反応速度」の中で扱う形を取っていました。
山本常信先生の非平衡統計力学の取り扱いに倣い、
輸送係数として反応速度定数を考える視点を獲得してもらえればという、
ちょっと大きな構想もありました(当時担当した杉本さんなどは熱心)。
けれども学生諸君にはいささか遠大にすぎる話のようで、
2014年度からは「反応速度」から切り離し、
準備実験の中で扱うことになったのです。
「空気抵抗」と空気の粘度
この実験では「空気抵抗」と空気の粘性力の相違をつかんでおくことが、
事態を理解する上で重要になります。
ガラス管の中に入れた羽根が、
ガラス管を真空にひくとストンと落ちてくるという実験はよく知られていますが、
こういう現象で問題になっているのは「空気抵抗」であって粘度ではありません。
事態を決めているのは、
ほとんど気体の質量密度であって、
気体の”化学的”な性質ではないのです。
同様にたとえば台風が来てものが吹き飛ばされるというのも、
気体の粘度はほとんど無関係です。
そもそもが、気体や液体の粘性による抵抗は、
あまり大きいものではありません。
球に働く抵抗力の表現として有名なストークスの式 \(6\pi \eta r v \) を知っている人も多いでしょう。
この式に従えば、仮に空気中で半径 5 cm ぐらいのボールが 10 m/s で運動しているとすると、
粘性抵抗は空気の粘度が0.02 mPa sぐらいですから 2 × 10-4 N にしかなりません。
ボールの重さを 100 g として、粘性抵抗による減速では1分たって速度が1/1000 ぐらい遅くなる程度です。
この一方、
ボールの周りで空気の流れの向きが大きく変わる状況を考えましょう。
ボールの前面で 10 m/s の流れが、後方ではほとんど止まっているような状態であれば、
ボールにかかる力は、単位時間当たり受け取る運動量ですから、
断面積に空気の密度と速度の2乗をかけて、
4 π × (5 cm)2 × 1.2 kg m-3 × (10 m/s)2 = 4 N
ぐらい。
剛速球で50 m/s であれば、100 N ぐらいにはなる勘定で、
粘性力の何万倍も大きな力が働きます。
真空中で羽根がストンと落ちてくる話で問題になっているのは、
この「空気抵抗」なわけです。
なぜ理論式が精度よく成立するのか
この実験で一番不思議なのは、
いい加減な装置で、
すごく適当に実験しているのに、
きれいな直線関係が得られてしまうところではないでしょうか?
たとえば温度を一定に保つ努力をしているわけではありませんし、
気体の膨張、圧縮にともなう温度変化もあるはずです。
温度変化についていうと、
最初に減圧する過程は、
断熱膨張でかなりの温度低下が起きるはずです
(1 kPa まで断熱可逆膨張させれば、TP1/γ - 1 = const より、
温度は 150 K ぐらいまで下がる。
実際には可逆膨張ではないのでここまでは下がらない)。
ただし全圧が低いので、かりに 1 kPa まで減圧したとして、50 K 下がったとして 0.2 kPa の低下です。
これは圧力計の誤差範囲。
そして圧力が低ければ熱容量が小さいので、
温度は急速に回復するでしょう。
その後の流通管を通じての空気の流入は、
いわゆるジュール-トムソン過程で、
理想気体であれば温度変化は無視でき、
空気の場合 100 kPa 程度の変化では検知できるレベルではありません。
たぶん問題なのは、
流通管の中の流れが、
粘性流の条件を満たしているかどうかでしょう。
ここは難しいところで、
実験的に確認するのが一番です。
今のところ、
致命的な問題はないようですが、
ブタンと空気の粘度の比が少し低めに出たりするあたりなど、
検討の余地はたくさん残されています。
準備実験のページへ