2020.5
吉村洋介
7. 弱酸・弱塩基の解離平衡とpH
7-2-2 弱酸・弱塩基の強塩基・強酸によるpH滴定
弱塩基(トリス)を取り扱うグループは文中の語句を{}で囲ったものに読み替える。
<操作>
- 200 mLのビーカーに0.1 mol/L酢酸溶液{トリス溶液}20 mLをとり、イオン交換水80 mLを加えてpHを測定する。
- マグネチック・スターラーで攪拌しながら0.2 mol/L水酸化ナトリウム溶液{塩酸}を加えて、pH変化を測定する。
最初の2-3点は 0.2 mL 滴下ごとに、その後は 0.5 mL 滴下ごとにpHを測定する。
ただし、当量点近傍ではpHが大きく変動するので、0.1-0.2 mL 滴下ごとにpHを測定する。
pH 11{pH 3}前後まで滴定する。
<検討>
- 横軸に加えた水酸化ナトリウム溶液{塩酸}の体積、縦軸にpHをとり、酢酸{トリス}の滴定曲線を描く。
- グランプロットを行って当量点を定め、滴定曲線から酢酸{トリスの共役酸}の酸解離定数 pKa を求めよ*1。
- 得られたpKa値を用いてHenderson-Hasselbalchの式
\begin{equation}
{\rm{pH = p}}K_{\mrm{a}} + \log \mrm{\frac{[量論から計算される共役塩基量]}{[量論から計算される共役酸量]}}
\label{eq:H-H}
\end{equation}
を滴定曲線上にプロットし比較せよ。
- pHの値を加えたアルカリ量{酸量}に対して微分し、その逆数を加えた水酸化ナトリウム溶液{塩酸}の体積に対してプロットすると放物線がえられる。
その理由を説明せよ。また実際にデータから微分量を計算してプロットし確かめよ。
*1 Henderson-Hasselbalchの式から、当量の半分だけの水酸化ナトリウム溶液{塩酸}を加えた時のpHの値が、
酢酸{トリスの共役酸}のpKaに相当する事がわかる。
弱酸{弱塩基}を強塩基{強酸}で滴定する時、滴定量が最初の弱酸{弱塩基}の解離度より十分大きく、
当量より十分小さい時、共役塩基{共役酸}濃度は強塩基{強酸}の滴定量と等しいと考えられることに注意。
<解説>:グランプロット Gran plot
Henderson-Hasselbalchの式で当量点近くの挙動を求める際には、当量点を精確に決めておくことが重要である。
いろいろ方法が考えられるがグランプロット Gran plot はよく知られた手法である。
図7-1 にグランプロットの例を示す。酢酸を水酸化ナトリウムで滴定する場合であれば、
グランプロットでは水酸化ナトリウムの滴下量 vNaOH に対し、
水酸化ナトリウム滴下量に水素イオン濃度をかけたもの vNaOH10-pH をプロットし、
当量点以下の直線部分と横軸の交点を当量点とする。
これは[Na+][H+](≈ [CH3COO-][H+] = Ka[CH3COOH])
を [Na+](≈ [CH3COO-] ≈ [CH3COOH]0 - [CH3COOH])
に対してプロットすることに相当している。
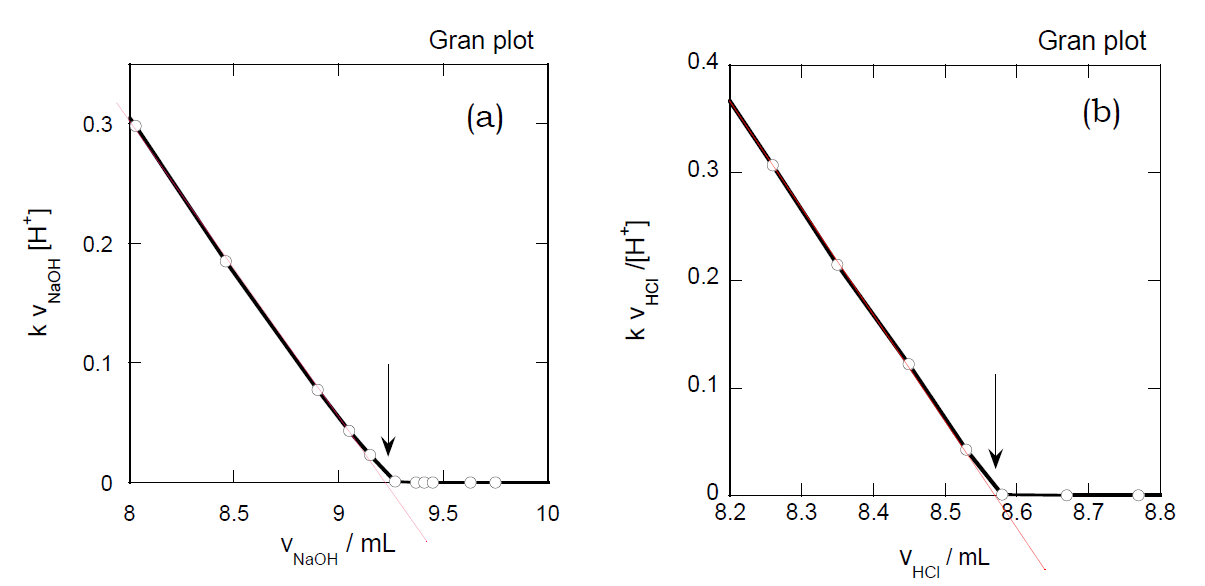
図7-1. グランプロット例。(a)は0.02 mol/L酢酸溶液を0.2 mol/L水酸化ナトリウム溶液で、
(b)は0.02 mol/Lトリス溶液を0.2 mol/L塩酸で滴定した場合のもの。
弱酸・弱塩基の強塩基・強酸によるpH滴定のはなし
この課題は2人一組で取り組んでもらい、
実験結果の解析用に用意したエクセルのシート
(酢酸組用とトリス組用があります)を完成すれば、
一通り実験課題はこなせたことになります。
ここではその基礎となる「理論」について説明しておきましょう。
ヘンダーソン-ハッセルバルヒの式の成立事情
ここで扱うことになるのは、
酢酸やトリスなど弱酸・弱塩基の解離平衡 HA ⇌ H+ + A- と水の解離平衡(自己プロトリシス)
H2O ⇌ H+ + OH-
が並行して起きる系になります。
こうした系の取り扱いについては、
すでに何度か聞いたことのある人も多いでしょうが、
ちょっと復習も兼ねて式の導出を見ておきましょう。
話を具体的にするために、酢酸に水酸化ナトリウム溶液を滴下する場合を考えます。
また水酸化ナトリウム溶液を加えると溶液量が増えて濃度が変化しますが、
影響は小さいので溶液量は一定とします(水酸化ナトリウムの固体を添加する形)。
さて滴定開始時に酢酸が濃度\(c_\mrm{A}\) あり、
ここに水酸化ナトリウム溶液を加え、
溶液中のナトリウムイオン濃度が \(\mrm{[Na^{+}]}\)
になったとします。
すると次の関係が成り立ちます:
\[
c _\mrm{A} = \mrm{[HA] + [A^{-}]} ,
\]
\[
\mrm{[Na^{+}] + [H^{+}] = [A^{-}] + [OH^{-}]} ,
\]
\[
K_{\mrm{a}} = \mrm{\frac{[H^{+}][A^{-}]}{[HA]}},
\]
\[
K_{\mrm{W}} = \mrm{[H^{+}][OH^{-}]}
\]
ここで \(K_{\mrm{a}}\) は酢酸の解離定数(\(\mrm{p}K_{\mrm{a}} = 4.8\))、
\(K_{\mrm{W}}\) は水の自己プロトリシス定数(\(\mrm{p}K_{\mrm{W}} = 14.0\))です。
ここでこの関係式を整理して、次のナトリウムイオン濃度と水素イオン濃度の関係式を得ます。
\begin{equation}
\mrm{[Na^{+}]} = -\mrm{[H^{+}]} + \frac{c _\mrm{A} K_{\mrm{a}}} {\mrm{[H^{+}]} + K_{\mrm{a}}} + \frac{K_{\mrm{W}}}{\mrm{[H^{+}]}}
\label{eq:rigorous}
\end{equation}
ヘンダーソン-ハッセルバルヒの式 \eqref{eq:H-H} は、
ここで
\begin{equation}
\mrm{[Na^{+}]} \gg \mrm{[H^{+}]} \gg K_{\mrm{W}}/\mrm{[H^{+}]} = \mrm{[OH^{-}]}
\label{eq:H-Hineq}
\end{equation}
として、次のように簡単化したことに相当しています:
\begin{equation}
\mrm{[Na^{+}]} = \frac{c _\mrm{A} K_{\mrm{a}}} {\mrm{[H^{+}]} + K_{\mrm{a}}}
\label{eq:H-Hrev}
\end{equation}
この式を少し変形して、\(c_\mrm{B} = \mrm{[Na^{+}]}\) とおいて少し一般的な風にすると
\[
\mrm{[H^{+}]} = \frac{K_{\mrm{a}} (c _\mrm{A} - c _\mrm{B})} {c _\mrm{B}}
\]
\begin{equation}
\mrm{pH} = \mrm{p}K_{\mrm{a}} + \log \frac{c _\mrm{B}}{c _\mrm{A} - c _\mrm{B}}
\label{eq:H-Hph}
\end{equation}
とすれば、ヘンダーソン-ハッセルバルヒの式としてよく見る 式\eqref{eq:H-H} であることは明かでしょう。
実際にどれぐらいこの近似がよいのか、確認してみた結果を下に示します。
|
|
|
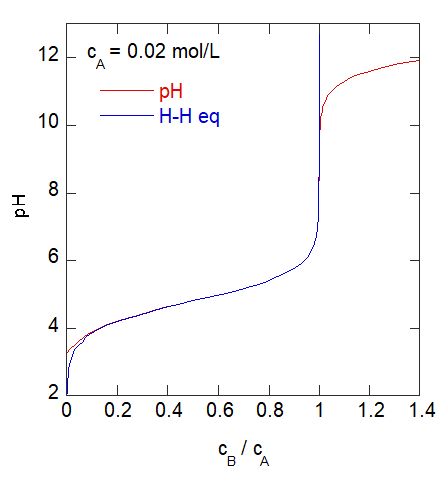
近似を使わずに得た pH の挙動(赤線)とヘンダーソン-ハッセルバルヒの式(青線)。
酢酸濃度 cA = 0.02 mol/L
|
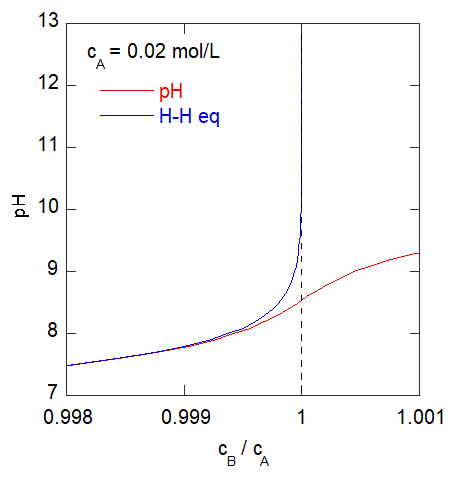
当量点近傍での挙動。
当量点の 1/1000 近くのところからはずれてくる。
|
初期の酢酸濃度が 0.02 mol/L で、ほぼ実験条件通りですが、
当量点のごく近傍、1/1000 ぐらいのところまで、
ヘンダーソンハッセルバルヒの式が成立していることが分かります。
実際の実験条件に照らせば、当量点の手前 0.01 mL のところまで、
ヘンダーソンハッセルバルヒの式で pH 変化はおおむね説明できるわけです。
当量点近傍では pH が 8 付近なわけですが、
先の厳密な式 \eqref{eq:rigorous} は、このとき水素イオン濃度が低く無視でき、次の関係式に書き換えられます
(くどいようですが \(c_\mrm{B} = \mrm{[Na^{+}]}\) です)。
\[
c_\mrm{B} - c _\mrm{A} \approx \frac{K_{\mrm{W}}}{\mrm{[H^{+}]}} = \mrm{[OH^{-}]}
\]
ですから当量点の近傍で cA - cA >> [OH-] の条件が破れるようになると、
無視していた水酸化物イオンの寄与が現れる、ヘンダーソン-ハッセルバルヒの式が外れてくることになります。
ここでは cA = 0.02 mol/L にとっていますから、
pH 8 での水酸化物イオン濃度 10-6 mol/L から、
およそ 1/1000 ぐらいから外れてくるというのは妥当な線です。
酢酸濃度がもっと高くなれば、
より当量点近傍まで、ヘンダーソン-ハッセルバルヒの式が成立することになります。
pH 滴定における pH の変動率
ヘンダーソン-ハッセルバルヒの式 \eqref{eq:H-Hph} (あるいは式 \eqref{eq:H-H})からは、
強塩基滴下量に対する pH の応答について、次の簡単な関係を得ることができます。
\[
\frac{\rmd~ \mrm{pH}}{\rmd~ c _\mrm{B}} = \log \mrm{e} \left( \frac{1}{c _\mrm{B}} + \frac{1}{c _\mrm{A} - c _\mrm{B}} \right)
= \frac{\log \mrm{e} ~c _\mrm{A}}{c _\mrm{B} (c _\mrm{A} - c _\mrm{B}) }
\]
この逆数をとると上に凸の放物線になっていて、\(c _\mrm{B} = c _\mrm{A}/2 \) で最大値を取ります。
\[
\log \mrm{e} ~c _\mrm{A} \frac{\rmd~ c _\mrm{B}}{\rmd~ \mrm{pH}} = - \left( c _\mrm{B} - \frac{c _\mrm{A}}{2} \right)^2 + \frac{c _\mrm{A}^2}{4}
\]
あるいは
\begin{equation}
\log \mrm{e} ~\frac{1}{c _\mrm{A}} \frac{\rmd~ c _\mrm{B}}{\rmd~ \mrm{pH}} = - \left( \frac{c _\mrm{B}}{c _\mrm{A}} - \frac{1}{2} \right)^2 + \frac{1}{4}
\label{eq:bufcap}
\end{equation}
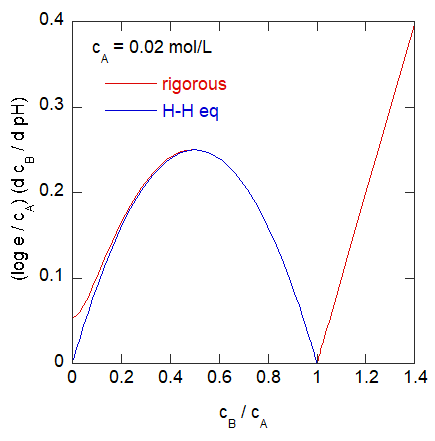
右図には、厳密な式 \eqref{eq:rigorous} から計算した値と、上のヘンダーソン-ハッセルバルヒの式からえた式 \eqref{eq:bufcap} を比較してみました。
おおむねね当量点以下ではよい近似になっていることが確認できます。
この \(\rmd ~c_\mrm{B} / \rmd~ \mrm{pH}\) という量は、pH を 1 変化させるのに、単位体積当たり必要な塩基の量に対応していて、
(微分)緩衝能と呼ばれるものです。
この値が大きいほど溶液の pH が安定しているわけで、
ここで見た酢酸と酢酸ナトリウムの混合系のような単純な系では、
緩衝能は共役酸と塩基の量が等しい時に最大となり、
その時の緩衝能の共役酸・塩基の総濃度 cA の (ln 10)/4 ≈ 0.58 倍になります。
酸解離定数の実験値
pH 滴定で得られた酸解離定数 pKa の値
| 物質 |
実験値 |
文献値 |
| 酢酸 |
4.66 ± 0.04 |
4.756 |
| トリス |
8.12 ± 0.05 |
8.071 |
文献値は CRC Handbook 2012 から 25 °C の希薄水溶液での値。
実際に pH 滴定のデータを解析してえられる酸解離定数 pKa の値を、右の表に示しました
(2018年度の学生さんたちの結果。これまでも同様の結果がえられています)。
これと手元のデータブックなどとを比較してみると、
酢酸については少し小さめ、トリスについては少し大きめの値になっていることがわかります。
このちがいは単に実験誤差や、pH の測定上の問題ではなく、
ここまでの議論では等閑に付してきた、電解質溶液の活量に大きな原因があります。
電解質溶液は、非電解質溶液に比べて非理想性の影響が大きく、
0.01 mol/L 程度の溶液でも1割程度の偏差が現れます(非水溶液ではもっと大きくなる)。
この偏差は低濃度(< ~ 0.01 mol/L)ではおおむね電解質の濃度 \(c\) の平方根に比例するとみてよく、
今回のケースではイオン X の活量 |X| と濃度 [X] の間には、おおむね次の関係が成り立っているとみられます
(X は1価のイオン。
1:1 電解質なのでイオン強度は濃度と等しいと見なせます。
詳細は手近な分析化学や物理化学の教科書で「デバイ-ヒュッケルの極限則」を調べてみてください)。
\begin{equation}
\log |\mrm{X}| = \log (\gamma [\mrm{X}]) \approx \log [\mrm{X}] - 0.5 \sqrt{c / \mrm{mol ~ L^{-1}}}
\label{eq:DH}
\end{equation}
今回の場合、pH 滴定では電解質の濃度 \(c\) が ~0.02 mol/L 程度になっていますから、
pKa には0.05 程度の影響が出てくることになります。
それがどのように表れてくるかですが、酸解離平衡 HA ⇌ H+ + A の解離定数は次のように書けます:
\begin{equation}
\mrm{p} K_\mrm{a} = \mrm{pH} - \log \frac{|\mrm{A}|}{|\mrm{HA}|}
= \mrm{pH} - \log \frac{[\mrm{A}]}{[\mrm{HA}]} \mp \log \gamma
= \mrm{p} K_\mrm{a} (\mrm{exp}) \mp \log \gamma
\label{eq:pKax}
\end{equation}
ここで\(\mrm{p} K_\mrm{a} (\mrm{exp})\) は今回の実験で求めた pKa で、
複号\(\mp\) は共役塩基 A がイオンの場合(酢酸)に\(-\)、
共役酸 HA がイオンの場合(トリス)に\(+\) を取ります。
ここで log γ がおよそ -0.05 程度なわけですから、
実験で求めた pKa は、酢酸では希薄溶液での pKa より 0.05 程度小さく、
トリスでは 0.05 程度大きくなるわけです。
このような電解質溶液の非理想性の影響は「塩効果」として知られ、
以前は酸塩基指示薬の解離定数に対する塩効果の実験なども行っていました。
文献値との偏倚については、これ以外にも温度の影響
(トリスの酸解離の ΔH が +47.45 kJ/molであるのに対し、
酢酸の ΔH はほぼゼロ -0.41 kJ/mol。
J. Phys. Chem. Ref. Data 31, 231 (2002))、
や二酸化炭素の影響など、いろいろ考えるべきことはあるのですが、まあこのあたりで・・・
弱酸・弱塩基の解離平衡とpHのページへ