|
|
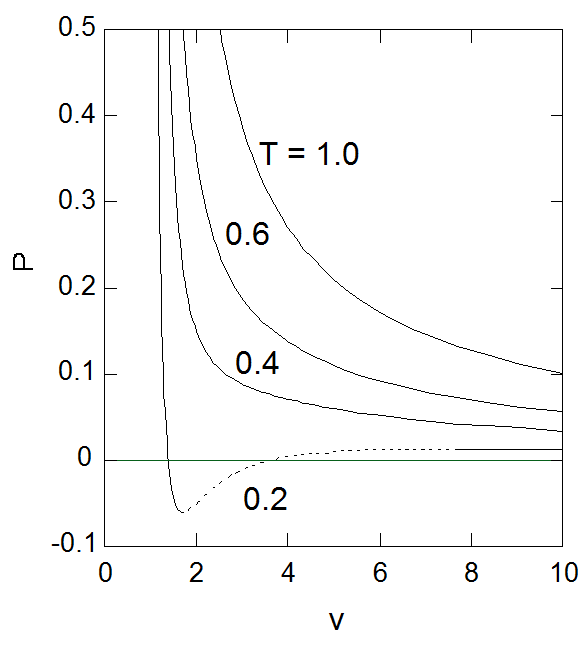
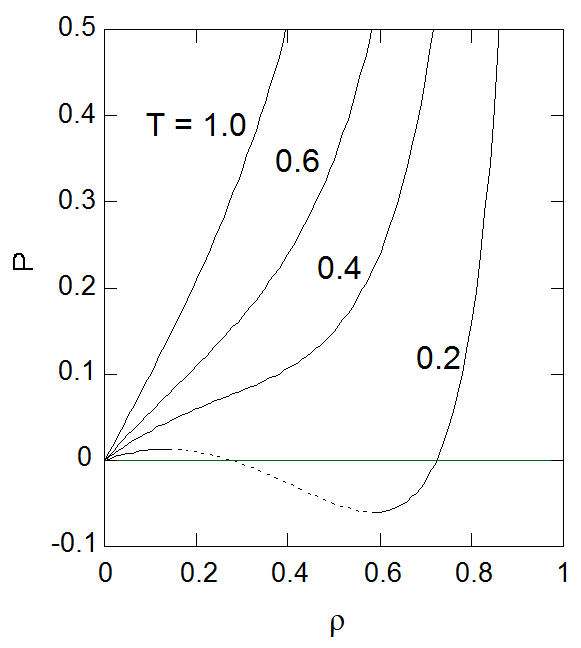
| 図1-1. 横軸にモル体積を取ったファンデルワールス状態方程式の等温線。 \(T = 0.2\) では機械的不安定性が現れる。 | 図1-2. 横軸に密度を取ったファンデルワールス状態方程式の等温線。 モル体積を用いた場合より、低密度での挙動がより鮮明になる。 |
ファンデルワールス状態方程式としてもっぱら流布しているのは、次の形のものでしょう:
\begin{equation} (P + \frac{N^2 a}{V^2}) (V - Nb) = N R T \end{equation}
ここで\(P\)は圧力、\(V\)は体積、\(T\)は熱力学温度、\(N\)は物質量(ぼくの若いころはモル数と呼んでいました)で、 \(R\)は気体定数、\(a\)と\(b\)は流体を特徴づける定数です。 この表記は中学校でも習う理想気体の状態方程式 \(PV = NRT\) で圧力、体積に修飾を加えた形をしていて、 学生の取っつきがいいようです。
これで、別に悪いわけではないのですが、示強変数である\(P\)、\(T\)と示量変数である\(V\)、\(N\)が共存していて、 いささか見通しが悪い形といえるでしょう。 むしろモル体積\(v = V/N\)を導入して、 次のような形に書いた方がすっきりします:
\begin{equation} (P + \frac{a}{v^2}) (v - b) = R T \end{equation}
この形で議論を進めてもいいのですが、圧力\(P\)に注目して議論する立場からは、もっとあからさまに次式のように表現した方が便利です:
\begin{equation} P = \frac{RT}{v - b} - \frac{a}{v^2} \end{equation}
また理想気体を扱うことを考えると、体積が十分大きな状態、\(v\)がとても大きな状態を扱うことになるので、 密度\(\rho = N/V = 1/v\) を使う方が便利です。 密度というのはいろんな意味で使われますが、ここでは単位体積当たりの物質量を意味するものとします。 密度を使うとファンデルワールス状態方程式は次の形になります:
\begin{equation} P = \frac{R \rho T}{1 - b \rho} - a \rho^2 \label{eq:vdweq} \end{equation}
このままで議論を進めてもいいのですが、密度、圧力、温度の単位をうまく選ぶことで、 ファンデルワールス状態方程式はもっと簡単な形に書くことができます。 式を少し変形すると次の式を得ることができます。
\begin{equation} P/(ab^{-2}) = \frac{R T / (ab^{-1})}{v/b - 1} - \frac{1}{(v/b)^2} \end{equation}
モル体積の単位を\(b\)、モルエネルギー(物質量当たりのエネルギー)の単位を\(ab^{-1}\)にとるなら、 圧力の単位は\(ab^{-2}\)になります(圧力× 体積がエネルギーになることに注意ください)。 こうすることで、あからさまに系を特徴づける係数\(a\)と\(b\)を表に出す必要がなくなります。 温度を表示する上でエネルギーの単位を気体定数 \(R\)にとる(モルエネルギー/\(R\) =温度の関係にあることに注意)ことで式はさらに簡単になり、 ファンデルワールス状態方程式は次の形に整理できます:
\begin{align} P &= \frac{T}{v - 1} - \frac{1}{v^2} \\ &= \frac{\rho T}{1 - \rho} - \rho^2 \end{align}
つまり式\eqref{eq:vdweq} で次のようにおいたことに相当しています:
\begin{equation} R = a = b = 1 \label{eq:vdw_unit} \end{equation}
以下では特に断らない限り、この単位系を用いてもっぱら記述することにします。 表記が面倒なので特に圧力や温度の記号を変えることはしませんので注意ください。 通常の単位系に直すには、圧力、温度、密度(そしてその逆数のモル体積)について
\begin{align} P &\to \frac{b^2}{a}P\\ T &\to \frac{Rb}{a}T\\ \rho &\to b \rho , ~~ v \to v/b \end{align}
という風に置き換えればよいわけです。 ここから導出される他の物理量についても容易に変換でき、例えば内部エネルギー \(U\) については \(P/\rho\) に対応していることに注意していただくと \(U \to (b/a)U\) と置き換えることになります。 なお注意すべきは、元の式のパラメーター \(a\) あるいは \(b\) を0に取った場合の挙動です。 \(a\) と \(b\) ともに0であれば理想気体に帰着するわけですが、たとえば \(a\) を0にとると式の中では圧力 \(P\) と温度 \(T\) は、 \(P/T\)といった形でしか登場が許されないことになります。 こうした事情に注意を払っていただく意味でも、随時、\(a\)、\(b\) を用いた記述も示すようにします(式の中では[ ]に囲んで示します)。
図1-1と1-2にはそれぞれモル体積と密度で表示した、 種々の温度における膨張・圧縮にともなう圧力の変化の様子を示しました。 両方とも同じ等温線を示しているのですが、横軸にモル体積を取った場合には、モル体積の増加に合わせてゆっくりと変化する圧力とどこまでも付き合わないといけませんが、 横軸に密度を取ると[0, 1)の限られた領域に話が集約されています。 初年級の物理化学の教科書ではPV仕事との対応もあってモル体積が変数として取られることが多いようですが、 密度で記述した方が全体の様子を見るには好ましいので、このお話ではもっぱら密度を変数として取ります。 実際、図1-1と1-2を比べてみても、密度で表示した方が低密度領域で理想気体の挙動(\(P = \rho T\))に近づくことがすぐ見て取れるでしょう。

|

|
| 図1-1. 横軸にモル体積を取ったファンデルワールス状態方程式の等温線。 \(T = 0.2\) では機械的不安定性が現れる。 | 図1-2. 横軸に密度を取ったファンデルワールス状態方程式の等温線。 モル体積を用いた場合より、低密度での挙動がより鮮明になる。 |
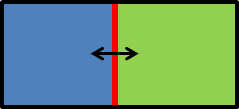
ファンデルワールス状態方程式は十分温度が低くなると、密度\(\rho\)の増加(体積\(v\)の収縮)にともない圧力が減少する領域が現れます(図1-1と1-2では\(T = 0.2\)の場合)。 こうした負の圧縮率を示す流体は不安定でただちに相分離を示します。 例えば容器に流体を入れておき、その中を仮想的な可動壁(ピストン)で2つに仕切ったとしましょう。 最初両方の圧力が釣り合った状態にあったとして、ほんの少しだけ壁が片方に移動したとします。 この時、体積が小さくなった側の圧力が高くなれば、壁を押し返して元に戻るわけですが、 負の圧縮率を示す場合にはそうはいきません。 逆に圧力が低くなり壁はさらに押し込まれてきます。 壁が押し込まれ体積が小さくなってまた圧力が下がり、またさらに壁が押し込まれる。 こうしたプロセスが密度の増加にともない圧力が高くなるという通常の状態に達するまで続き、 さらに圧力のつり合いが回復した時には密度の異なる2つの領域が存在するになる。 つまり気液の相分離が起きることになるわけです。 このように圧力のつり合いに関わって相が不安定になる挙動を機械的な不安定性mechanical instabilityと呼びます
流体の不安定性、気液の相分離挙動の起きるようになる温度を臨界温度critical temperature \(T_\rm{c}\)、 圧力を臨界圧力critical pressure \(P_\rm{c}\)、 また臨界温度、臨界圧力における流体の密度を臨界密度 critical density \(\rho_\rm{c}\)(この逆数が臨界モル体積 \(v_{\rm{c}}\))、 これらをまとめて臨界定数あるいは臨界パラメーターと呼びます。 後でも触れますが、ファンデルワールス状態方程式から臨界定数を求めるのは、 おそらく皆さんもおなじみのところでしょう。 後でも触れますが、臨界温度、臨界圧力、臨界モル体積は、それぞれ次のように表されます:
\begin{align} T_{\rm{c}} &= \frac{8}{27} ~&\left[ = \frac{8}{27} \frac{a}{Rb} \right] \\ P_{\rm{c}} &= \frac{1}{27} ~&\left[ = \frac{1}{27} \frac{a}{b^2} \right] \\ \rho_{\rm{c}} &= \frac{1}{3} ~&\left[ = \frac{1}{3 b} \right] \end{align}
ここから得られる臨界点での圧縮率因子\(P_{\rm{c}} /\rho_{\rm{c}} T_{\rm{c}} = P_{\rm{c}}v_{\rm{c}}/T_{\rm{c}} ~[ = P_{\rm{c}}v_{\rm{c}}/ R T_{\rm{c}}]\)は
\begin{equation} \frac{P_{\rm{c}}}{\rho_{\rm{c}} T_{\rm{c}}} = \frac{3}{8} \end{equation}
となり、多くの実在の流体の臨界点での圧縮率因子(およそ 0.28~0.30 )より大きいものの、 妥当なものになっているのはよく知られているところです。 また多くの物理化学の教科書に、ファンデルワールスが導いた、 この臨界定数を単位に取った次のような「換算状態方程式」が紹介されているのは皆さんもよくご存じでしょう:
\begin{equation} \Pi = \frac{8 \Theta}{3 \Phi - 1} - \frac{3}{\Phi^2} \end{equation}
ここで\(\Pi = P/P_\rm{c}\)、\(\Theta = T/T_\rm{c}\)、\(\Phi = v/v_\rm{c}\)です。 相挙動や臨界点近傍の挙動の議論だけならこの形でもよいのですが、 種々の条件下の熱力学的な関係式を記述す上では係数がいささかやっかいなので、 ここでは式 \eqref{eq:vdw_unit} で示した単位の取り方を用います。