|
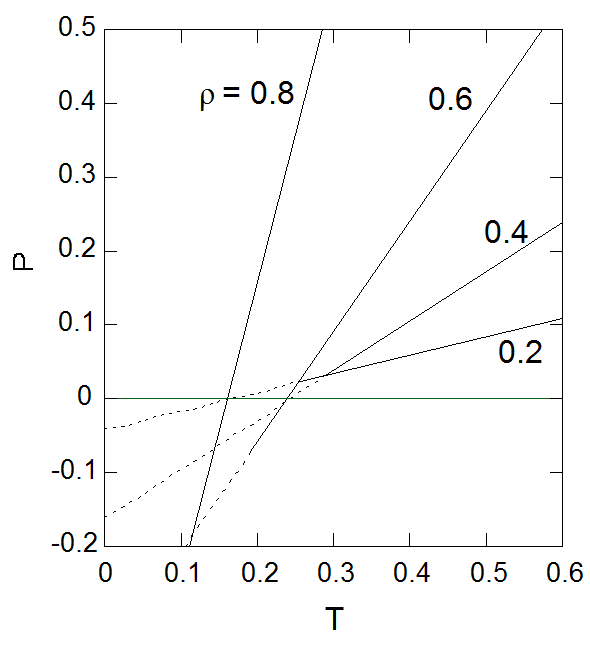
図2-1. ファンデルワールス状態方程式の等密度線。 図中破線の部分は機械的不安定性を示す領域。 |
圧力を温度・密度の関数として表示する\(P(T, \rho)\)という形で眺めた時、 ファンデルワールス状態方程式の大きな特徴は、温度に比例する項と温度に依存しない項からなっていることです。
\begin{align} P &= \frac{\rho T}{1 - \rho} - \rho^2 \\ &= T f(\rho) - \rho^2 \end{align}
以下でもしばしば登場するので、\(\rho/(1 - \rho) [ = 1/(v - 1)]\) を\(f(\rho)\)と表記することにします。 密度一定(モル体積一定)の条件で、圧力の温度微分は温度によらず一定で、 温度-圧力の間には直線関係が成立します:
\begin{equation} \left( \frac{\partial P}{\partial T} \right)_{\rho} = f(\rho) = \frac{\rho}{1 - \rho} \end{equation}

|
図2-1. ファンデルワールス状態方程式の等密度線。 図中破線の部分は機械的不安定性を示す領域。 |
等容(isochore)条件での温度変化に対する圧力の直線関係は、多くの流体でおおむね成り立つことが知られています。 また関数\(f(\rho)\)は正で、またその高階の微分も正になります。
\begin{equation} \frac{\partial^{(n)} f(\rho)}{\partial \rho^{(n)}} = f^{(n)}(\rho) = \frac{n!}{(1 - \rho)^{n+1}} \gt 0 \label{eq:fderivatives} \end{equation}
圧力の密度微分については次の関係が成り立ちます:
\begin{align} \frac{\partial P}{\partial \rho} &= T f'(\rho) - 2 \rho \\ &= \frac {T}{(1 - \rho)^2} - 2 \rho &~\left[ = \frac {RT}{(1 - b\rho)^2} - 2 a\rho \right] \\ &= \frac {P}{\rho (1 - \rho)} - \frac {\rho (1 - 2\rho)}{1 - \rho} &~\left[ = \frac {P}{\rho (1 - b\rho)} - \frac {a\rho (1 - 2b\rho)}{1 - b\rho} \right] \\ \end{align}
ビリアル係数 \(B_k\) は、下式のように圧縮率因子\(P/\rho T\)を密度のベキ級数で展開した時の係数に相当し (\(B_1 = 1\))、
\begin{equation} \frac{P}{\rho T} = 1 + B_{2} \rho + B_{3} \rho^2 + \cdots \end{equation}
次のように表現できます:
\begin{align} B_{2} &= 1 - \frac{1}{T} ~\left[ = b - \frac {a}{RT} \right] \\ B_{k} &= 1 ~\left[ = b^{k-1} \right] ~~k \ge 3 \end{align}
第2ビリアル係数が0になる温度(ボイルBoyle温度)\(T_{\rm{B}}\)は
\begin{equation} T_{\rm{B}} = 1 ~\left[ = \frac {a}{Rb} \right] \end{equation}
先の\(f(\rho)\)の高階の微分について見た式 \eqref{eq:fderivatives} の結果は、 高次のビリアル係数がすべて正で温度に依存しないことを意味しているわけです。
等温圧縮率\(\kappa_{T}\)は次式で定義されています:
\begin{equation} \kappa_{T} = -\frac{1}{v} \left( \frac{\partial v}{\partial P} \right)_{T} = \frac{1}{\rho} \left( \frac{\partial \rho}{\partial P} \right)_{T} \end{equation}
理想気体では等温圧縮率\(\kappa_{T}\)は\(1/P = 1/\rho T\)です。 ですから先の(5)式で見た圧力の密度微分の逆数に対応し、あからさまな形で表記すると次のようになります:
\begin{align} \rho \kappa_{T} &= \frac{\partial \rho}{\partial P} \\ &= \frac{1}{T f'(\rho) -2\rho} = \frac{(1 - \rho)^2}{T - 2\rho (1 - \rho)^2} ~\left[ = \frac{(1 - b\rho)^2}{RT - 2a \rho (1 - b \rho)^2} \right] \\ &= \frac{\rho (1 - \rho)}{P - \rho^2 (1 - 2\rho)} ~\left[ = \frac{\rho (1 - b\rho)}{P - a \rho^2 (1 - 2b \rho)} \right] \end{align}
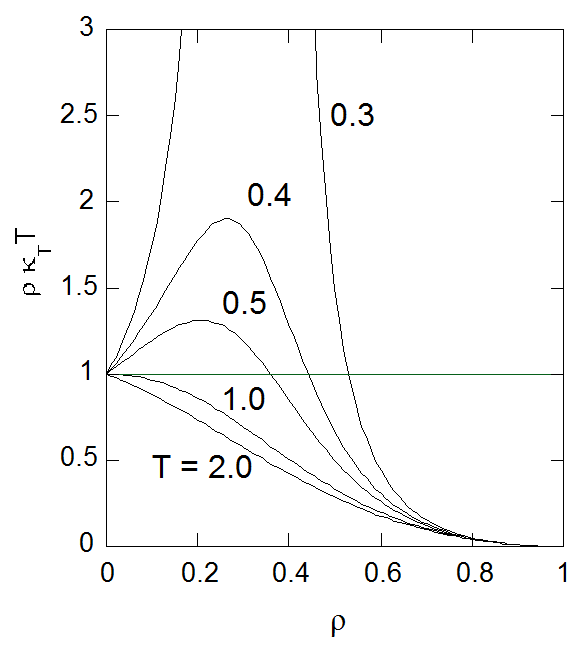
等温圧縮率に密度と温度をかけたもの\(\rho \kappa_{T} T (= T \partial \rho/ \partial P)\)は理想気体では1になります。 この形で等温圧縮率の密度依存性を示したものを図に示します。 低密度側ではボイル温度\(T_{{\rm B}} ( = 1) \)以下では密度を上げていくと\(\rho \kappa_{T} T \)は大きくなり、 以上では小さくなります(ビリアル展開の第2ビリアルの項まで取ると\(\rho \kappa_{T} T = 1 - 2B_{2} \rho\))。 図にもあるように温度を下げると圧力の密度依存性がゼロになる(その逆数の圧縮率は無限大になる)ところが出現します。 そうした挙動を反映して密度の中間領域で圧縮率が非常に大きくなる領域が存在することが分かります。
|
図2-2. 種々の温度における等温圧縮率\(\kappa_{T}\)の密度依存性。 図には密度と温度をかけた \(\rho \kappa_{T} T\) の形で表してある。 低密度の極限で \(\rho \kappa_{T} T\) は1であり、高密度の極限\(\rho \to 1\)では0になる。 ボイル温度以下では低密度側では、密度の増加とともに大きくなり、 臨界温度(\(T_{\rm{c}} = 8/27\))以下では臨界密度(\(\rho_{\rm{c}} = 1/3\))付近で発散する挙動を示す。 |
等温圧縮率が負になると、系は機械的な不安定性を示します。 機械的な不安定性を示す領域の境界線(スピノーダル曲線と呼びます)は、 \(TP\)面で密度をパラメーターに用いて次のように与えられます(式の分母が0になる条件):
\begin{align} T_{\rm{sn}}(\rho) &= 2\rho (1 - \rho)^2 \\ P_{\rm{sn}}(\rho) &= \rho^2 (1 - 2\rho) \\ \end{align}
幾何学的に見ると、\(TP\)面でのスピノーダル曲線は等密度線の包絡線に相当しています。 教科書的に言えば、包絡線はそもそもの状態方程式から与えられる等密度線の関係式\(F(P, T, \rho) = 0\)と、 それをパラメーター\(\rho\)について偏微分したものが0になるという要件\(\partial F(P, T, \rho)/\partial \rho = 0\)で与えられます。 つまり
\begin{align} F(P, T, \rho) &= P - T f(\rho) + \rho^2 = 0 \\ \frac{\partial F(P, T, \rho)}{\partial \rho} &= -T f'(\rho) + 2\rho = 0 \\ \end{align}
ここで後者の式がスピノーダル曲線の条件\(\partial P/ \partial \rho = 0\)と一致していることがわかります。
|
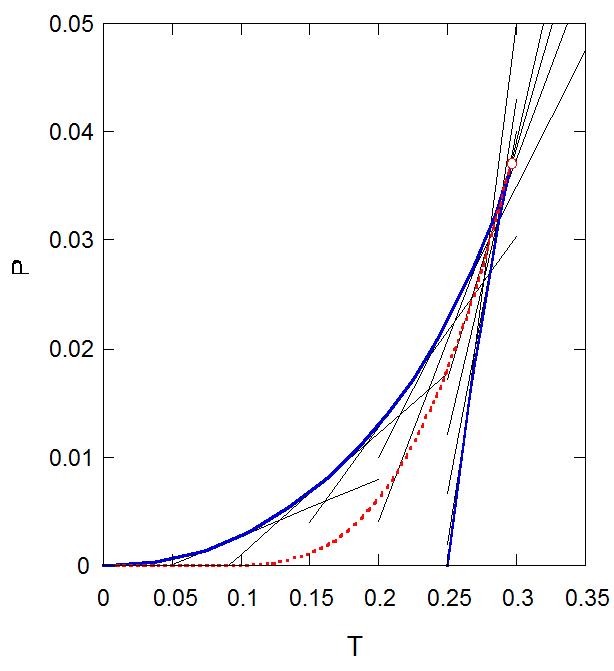
図2-3. \(TP\)面におけるスピノーダル曲線(青い実線)。 図にはいくつかの密度における等密度線も示してある。 赤い丸印は臨界点(\((T, P) = (8/27, 1/27)\))で、 赤い点線は後述する蒸気圧曲線(2相共存線)。 |
スピノーダル曲線上には尖点(カスプcusp)が存在し、 ちょうどここが臨界点に相当しています。 カスプの存在はスピノーダル曲線の式で、\((T_{\rm{sn}}(\rho), P_{\rm{sn}}(\rho))\) を密度について微分してみると
\begin{align} T'_{\rm{sn}}(\rho) &= 2 (1 - \rho) (1 - 3\rho) \\ P'_{\rm{sn}}(\rho) &= 2 \rho (1 - 3\rho) \end{align}
となることから、\(\rho\)を大きくしていくと\(\rho\ = 1/3\)でともに0となって符号が正から負に転じる (つまり法線方向のベクトルの向きが反転する)ことから直接確認できます。 ここが不安定性を示すようになる温度・圧力の最大値を与える点、臨界点になっています。 臨界パラメーターはすでに紹介したように次の通りです:
\begin{align} T_{\rm{c}} &= \frac{8}{27} ~&\left[ = \frac{8}{27} \frac{a}{Rb} \right] \\ P_{\rm{c}} &= \frac{1}{27} ~&\left[ = \frac{1}{27} \frac{a}{b^2} \right] \\ \rho_{\rm{c}} &= \frac{1}{3} ~&\left[ = \frac{1}{3 b} \right] \end{align}
なおスピノーダル曲線の接線が等密度線になるわけですが、これもスピノーダル曲線の接線の方程式が
\begin{equation} P'_{\rm{sn}}(\rho) (T - T_{\rm{sn}}(\rho)) = T'_{\rm{sn}}(\rho) (P - P_{\rm{sn}}(\rho)) \end{equation}
であることから、直接確認できます(点\((T_{\rm{sn}}, P_{\rm{sn}})\)を通り勾配\((\rmd P/\rmd T)_{\rm{sn}} = P'_{\rm{sn}}/T'_{\rm{sn}}\)の直線)。
ファンデルワールス流体の等密度線は温度を下げていった時、\(\partial P/\partial \rho = 0\)で機械的な不安定領域に達します。 ですから機械的な不安定領域を持たない等密度線は、スピノーダル曲線上の接線として始まり、 \(P\) あるいは \(T\) に対して増加する方向に延びる直線ということになります。
流体の等圧熱膨張率 \(\alpha_{P}\) は次式で定義されます:
\begin{equation} \alpha_{P} = \frac{1}{v} \left( \frac{\partial v}{\partial T} \right)_{P} = - \frac{1}{\rho} \left( \frac{\partial \rho}{\partial T} \right)_{T} \end{equation}
ここまでは機械的不安定性の条件から、もっぱら圧力の密度微分が0になることに注目して議論してきたわけですが、 密度の温度依存性、あるいは温度の密度依存性に注目しても同じような議論ができます。 それは次の関係からあきらかです:
\begin{align} \alpha_{P} &= - \frac{1}{\rho} \pdifA{\rho}{T}{P} = \frac{1}{\rho} \pdifA{\rho}{P}{T} \pdifA{P}{T}{\rho} \\ &= \kappa_{T} f(\rho) = \frac{1 - \rho}{T - 2\rho (1 - \rho)^2} \label{eq:expansibility} \end{align}
機械的な不安定性が起き、等温圧縮率が発散すると、等圧熱膨張率も発散します。 また機械的な不安定性が起きない限り(\(\kappa_{T} \gt 0\))、ファンデルワールス状態方程式は正の等圧膨張率 \(\alpha_{P} \gt 0\) を与えます。
等圧膨張率が負になること自体は、液体の水が 4°C 以下でも安定に存在するように、系の不安定性を直ちにもたらすわけではありません。 しかしファンデルワールス流体では、式 \eqref{eq:expansibility} の関係から等圧膨張率が負になることは等温圧縮率が負になることと直結しています。 われわれに身近な圧倒的多数の流体で負の膨張率が現れないのは、ファンデルワールス状態方程式がそうした液体の多数派の属性を反映しているからともいえるでしょう。